高斯函数
目录
1、高斯函数与正态分布
- 1.1 一维高斯函数
- 1.2 正态分布
- 1.3 二维高斯函数
2、高斯模糊原理
- 2.1 二维高斯函数求权重
- 2.2 权重矩阵
- 2.3 计算高斯模糊
3、高斯核函数
- 3.2 径向基函数RBF
- 3.3 高斯函数性质
4、高斯噪声
- 4.1 噪声
- 4.2 高斯噪声
高斯函数广泛应用于统计学领域,用于表述正态分布,在信号处理领域,用于定义高斯滤波器,在图像处理领域,二维高斯核函数常用于高斯模糊,在数学领域,主要用于解决热力方程和扩散方程。
1、高斯函数与正态分布
1.1 一维高斯函数

- a表示得到曲线的高度;
- b(μ)是指曲线在x轴的中心;
- c(σ)指width(与半峰全宽有关);
图形如下:

1.2 正态分布
高斯函数其实是一族函数,而满足正态分布的高斯函数如下所示
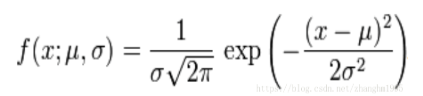

1.3 二维高斯函数(高斯分布、正态分布)
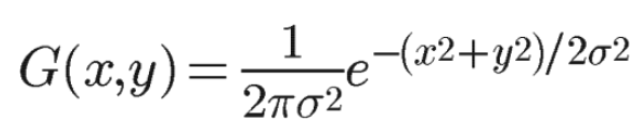
μ=0,即中心点就是原点。
二维高斯函数在计算机视觉领域用处广泛,利用0均值的二维高斯函数,可以生成高斯卷积核,用于图像处理中的高斯滤波,实现高斯模糊的效果,有效去除高斯噪声。
二维高斯函数的表达式和形状如下所示,为一个立体“钟状图”。

2、高斯模糊原理
模糊就是每隔像素取周边像素的平均值,在数值上是一种平滑作用,在图形上相当于产生模糊效果,中间点失去细节。

很显然,计算平均值时,取周边范围越大,模糊效果越强烈。
每个点都取周边像素的平均值,那么如何分配周边像素的权重呢?如果使用简单平均,不合理,这样忽略了图像像素之间的连续性和相关性。图像都是连续的,越靠近的点关系越密切,越远离的点关系越疏远,因此距离近的点权重大,距离远的点权重小。显然,正态分布是一种可取权重分布模式。
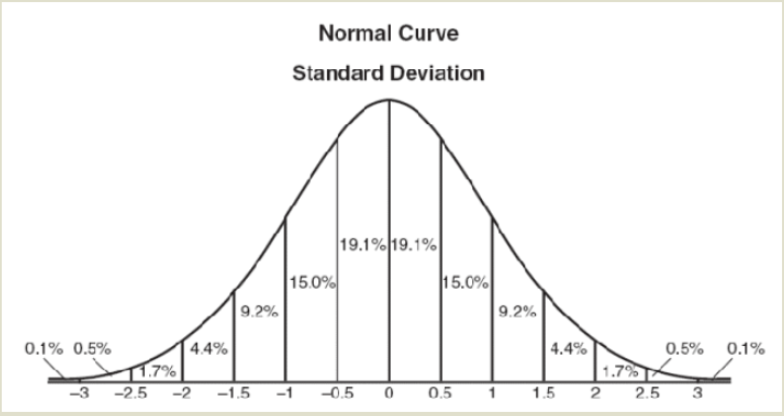
计算平均值时,将中心点作为原点,其他点按照其在正态曲线上的位置,分配权重,就可以得到一个加权值。
2.1 二维高斯函数
一维形式:

令中心点就是原点,即μ=0:
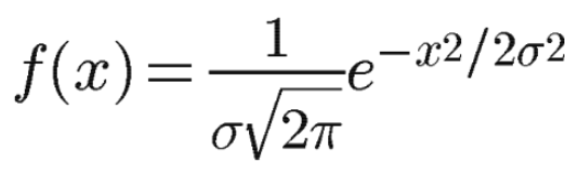
进而推导二维高斯函数:

2.2 权重矩阵
假定中心点的坐标是(0,0),那么距离它最近的8个点的坐标如下:
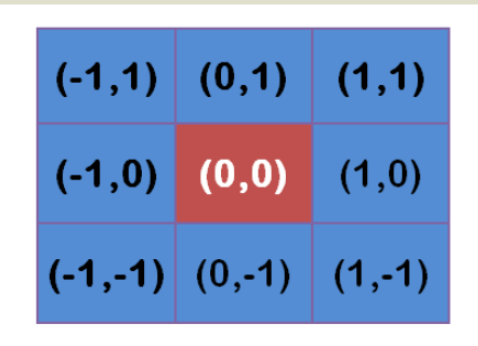
更远的点以此类推。
为了计算权重矩阵,需要设定σ的值。假定σ=1.5,则模糊半径为1的权重矩阵如下:
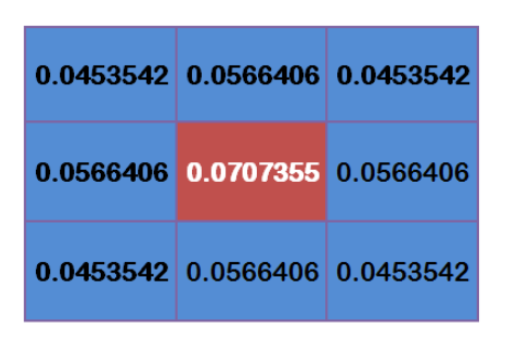
这9个点的权重总和等于0.4787147,如果只计算这9个点的加权平均,还必须让它们的权重之和等于1,因此上面9个值还要分别除以0.4787147,得到最终的权重矩阵。
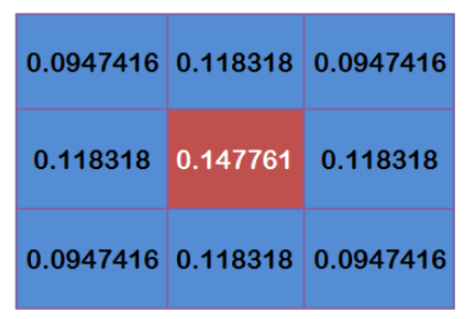
2.3 计算高斯模糊
假设现有9个像素点,灰度值(0-255)如下:
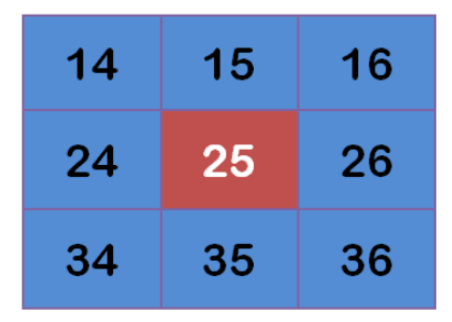
每个点乘以自己的权重值(协相关运算、矩阵点乘):

将这9个值加起来,就是中心点的高斯模糊的值。对所有点重复这个过程,就得到了高斯模糊后的图像。如果原图是彩色图片,可以对RGB三个通道分别做高斯模糊。
3、高斯核函数
3.2 径向基函数RBF
径向基函数 (Radial Basis Function 简称 RBF), 就是某种沿径向对称的标量函数。 通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数 , 可记作 k(||x-xc||), 其作用往往是局部的 , 即当x远离xc时函数取值很小。
最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/2*σ^2) } 其中xc为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。
3.3 高斯函数性质
高斯函数具有五个重要的性质,这些性质使得它在早期图像处理中特别有用。这些性质表明,高斯平滑滤波器无论在空间域还是在频率域都是十分有效的低通滤波器,且在实际图像处理中得到了工程人员的有效使用。高斯函数具有五个十分重要的性质,它们是:
1、二维高斯函数具有旋转对称性,即滤波器在各个方向上的平滑程度是相同的。
一般来说,一幅图像的边缘方向是事先不知道的,因此,在滤波前是无法确定一个方向上比另一方向上需要更多的平滑。旋转对称性意味着高斯平滑滤波器在后续边缘检测中不会偏向任一方向。
2、高斯函数是单值函数。这表明,高斯滤波器用像素邻域的加权均值来代替该点的像素值,而每一邻域像素点权值是随该点与中心点的距离单调增减的。这一性质是很重要的,因为边缘是一种图像局部特征,如果平滑运算对离算子中心很远的像素点仍然有很大作用,则平滑运算会使图像失真。
3、高斯函数的付立叶变换频谱是单瓣的。正如下面所示,这一性质是高斯函数付立叶变换等于高斯函数本身这一事实的直接推论。图像常被不希望的高频信号所污染(噪声和细纹理)。而所希望的图像特征(如边缘),既含有低频分量,又含有高频分量。高斯函数付立叶变换的单瓣意味着平滑图像不会被不需要的高频信号所污染,同时保留了大部分所需信号。
4、高斯滤波器宽度(决定着平滑程度)是由参数σ表征的,而且σ和平滑程度的关系是非常简单的。σ越大,高斯滤波器的频带就越宽,平滑程度就越好。通过调节平滑程度参数σ,可在图像特征过分模糊(过平滑)与平滑图像中由于噪声和细纹理所引起的过多的不希望突变量(欠平滑)之间取得折衷。
5、由于高斯函数的可分离性,大高斯滤波器可以得以有效地实现。二维高斯函数卷积可以分两步来进行,首先将图像与一维高斯函数进行卷积,然后将卷积结果与方向垂直的相同一维高斯函数卷积。因此,二维高斯滤波的计算量随滤波模板宽度成线性增长而不是成平方增长。
4、高斯噪声
4.1 噪声
一般默认噪声是高斯噪声,是为了更好的模拟未知的真实噪声。在真实环境中,噪音往往不是由单一源头造成的,而是很多不同来源的噪音复合体。假设,我们把真实噪音看成非常多不同概率分布的随机变量的加合,并且每一个随机变量都是独立的,那么根据Central Limit Theorem,他们的normalized sum就随着噪音源数量的上升,趋近于一个高斯分布。基于这种假设来看,采用合成的高斯噪音,是在处理这种复杂,且不知道噪音分布为何的情况下,一个既简单又不差的近似仿真。
噪声在图像上常表现为一引起较强视觉效果的孤立像素点或像素块。一般,噪声信号与要研究的对象不相关,它以无用的信息形式出现,扰乱图像的可观测信息。通俗的说就是噪声让图像不清楚。对于数字图像信号,噪声表为或大或小的极值,这些极值通过加减作用于图像像素的真实灰度值上,对图像造成亮、暗点干扰,极大降低了图像质量,影响图像复原、分割、特征提取、图像识别等后继工作的进行。
4.2 高斯噪声
概率密度函数服从高斯分布的一类噪声。如果一个噪声,幅度分布服从高斯分布,功率谱密度是均匀分布,则称为高斯白噪声。高斯白噪声的二阶矩不相关,一阶矩为常数,是指先后信号在时间上的相关性。
表现形式:



