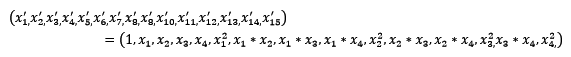4、特征预处理
通过特征提取,我们能得到未经处理的特征,这时的特征可能有以下问题:
- 不属于同一量纲:即特征的规格不一样,不能够放在一起比较。无量纲化可以解决这一问题。
- 信息冗余:对于某些定量特征,其包含的有效信息为区间划分,例如学习成绩,假若只关心“及格”或不“及格”,那么需要将定量的考分,转换成“1”和“0”表示及格和未及格。二值化可以解决这一问题。
- 定性特征不能直接使用:某些机器学习算法和模型只能接受定量特征的输入,那么需要将定性特征转换为定量特征。最简单的方式是为每一种定性值指定一个定量值,但是这种方式过于灵活,增加了调参的工作。例如one-hot编码,使用一个二进制的位来表示某个定性特征的出现与否。相比直接指定的方式,不用增加调参的工作,对于线性模型来说,使用哑编码后的特征可达到非线性的效果。
- 存在缺失值:缺失值需要补充。
- 信息利用率低:不同的机器学习算法和模型对数据中信息的利用是不同的,之前提到在线性模型中,使用对定性特征哑编码可以达到非线性的效果。类似地,对定量变量多项式化,或者进行其他的转换,都能达到非线性的效果。
一、无量纲化
无量纲化使不同规格的数据转换到同一规格。
常见的无量纲化方法有标准化和区间缩放法。标准化的前提是特征值服从正态分布,标准化后,其转换成标准正态分布。区间缩放法利用了边界值信息,将特征的取值区间缩放到某个特点的范围,例如[0, 1]等。
1、标准化
(1)零-均值规范化(z-score标准化/标准差)
经过处理的数据的均值为0,标准差为1。
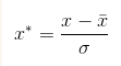
标准差分数可以回答这样一个问题:"给定数据距离其均值多少个标准差"的问题,在均值之上的数据会得到一个正的标准化分数,反之会得到一个负的标准化分数。
(2)中心化
x' = x - μ
(3)离散特征连续化
很多机器学习算法只能处理连续值特征,不能处理离散值特征,比如线性回归,逻辑回归等。最常见的离散特征连续化的处理方法是独热编码one-hot encoding。
第二个方法是特征嵌入embedding。一般用于深度学习中,比如对于用户的ID这个特征,如果要使用独热编码,则维度会爆炸,如果使用特征嵌入就维度低很多了。对于每个要嵌入的特征,我们会有一个特征嵌入矩阵,这个矩阵的行很大,对应我们该特征的数目。比如用户ID,如果有100万个,那么嵌入的特征矩阵的行就是100万。但是列一般比较小,比如可以取20。这样每个用户ID就转化为了一个20维的特征向量。进而参与深度学习模型。
(4)离散特征离散化
独热编码。
虚拟编码dummy coding,它和独热编码类似,但是它的特点是,如果我们的特征有N个取值,它只需要N-1个新的0,1特征来代替,而独热编码会用N个新特征代替。比如一个特征的取值是高,中和低,那么我们只需要两位编码,比如只编码中和低,如果是10则是中,01则是低。00则是高了,而独热编码需要三位。
(5)连续特征离散化
设置阈值。
2、区间放缩法(归一)
形象来说,标准化是按特征矩阵的行处理数据,归一化是按列处理。目的是样本向量在点乘运算或其他核函数计算相似性时候,拥有统一的标准,也就是都转化为单位向量。
(1)归一化
将数据值映射在[0,1]内。
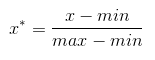
这种处理方法的缺点是若数值集中且某个数值很大,则规范化后各值接近于0,并且将会相差不大。
(2)平均归一化
x' = (x - μ) / (MaxValue - MinValue)
(3)小数定标
通过移动属性值的小数位数,将属性值映射到[-1, 1]之间,移动的小数位数取决于属性值绝对值的最大值。转化公式为:
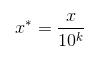
3、经验之谈
(1)如果对输出结果范围有要求,用归一化。
(2)如果数据较为稳定,不存在极端的最大最小值,用归一化。
(3)如果数据存在异常值和较多噪音,用标准化,可以间接通过中心化避免异常值和极端值的影响。
二、缺失值
1、删除
直接删除存在缺失值的数据条目。会造成浪费资源,如果原来样本就少的话,这样会导致样本不足,性能变差。
2、权重
给有缺失值的样本设一个权重,如果这个变量对最后的结果影响大,那么就可以通过权重来减小偏差,如果影响不大,这个权重也就不能减小偏差。
3、填补
(1)人工
(2)特殊值填充unknown
(3)均值填充
(4)聚类填充,如k近邻,将前k个对应属性值的均值填充进去
(5)使用可能的值来填充
(6)组合完整化
(7)回归,估计这个属性值
(8)多重插补
4、不处理
神经网络可以处理缺失值。
三、数据变换
常见的数据变换有基于多项式的、基于指数函数的、基于对数函数的。4个特征,度为2的多项式转换公式如下: