归并排序

归并排序

二分，比较与合并。

原理

采用递归和分治的思想，首先将数组二分成多个子序列，然后两两子序列进行比较与合并，使其合并为一个完全有序的序列。不断进行比较与合并，使子序列们最终合并为一个完整有序的序列。

分析

最佳：o(n) 
最坏：o(nlogn) 
平均：o(nlogn)

稳定，适用大规模，内存允许。

详细过程

当我们要排序这样一个数组的时候，归并排序法首先将这个数组分成一半。如图：

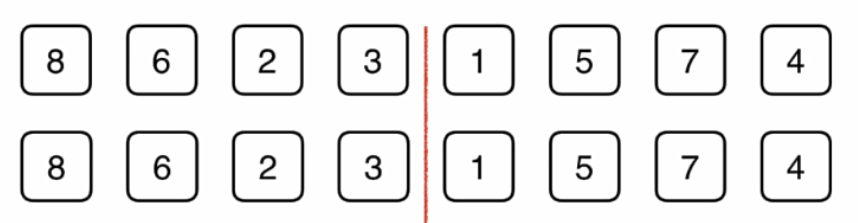
然后想办法把左边的数组给排序，右边的数组给排序，之后呢再将它们归并起来。当然了当我们对左边的数组和右边的素组进行排序的时候，再分别将左边的数组和右边的数组分成一半，然后对每一个部分先排序，再归并。如图：

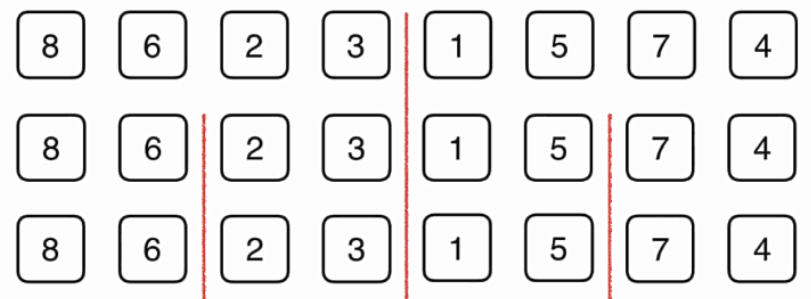
对于上面的每一个部分呢，我们依然是先将他们分半，再归并，如图：

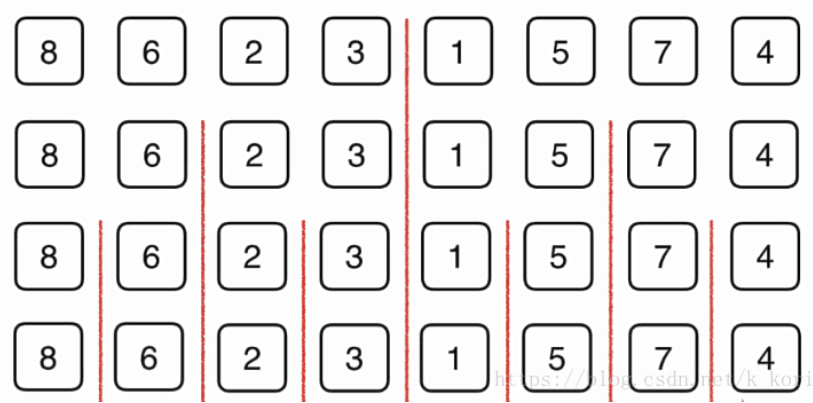
分到一定细度的时候，每一个部分就只有一个元素了，那么我们此时不用排序，对他们进行一次简单的归并就好了。如图：

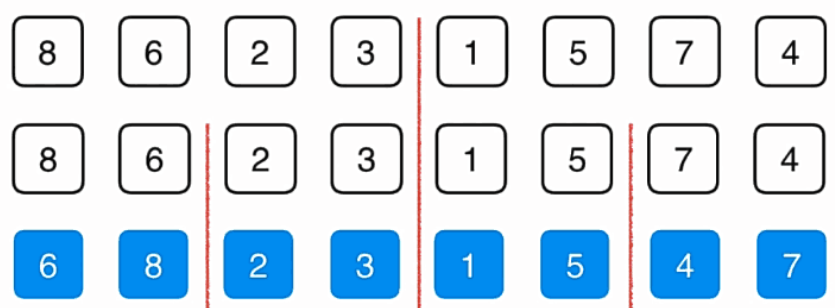
归并到上一个层级之后继续归并，归并到更高的层级，如图：

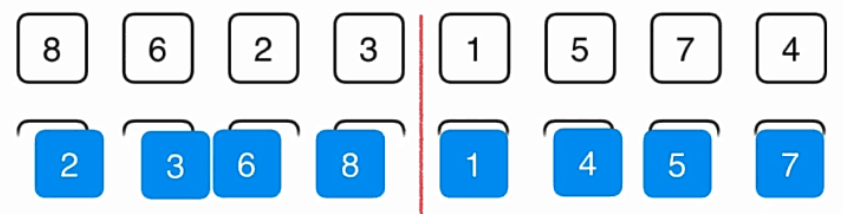
直至最后归并完成。

我们可以开辟一个临时数组来辅助我们的归并。也就是说他比我们插入排序也好，选择排序也好多使用了存储的空间，也就是说他需要o（n）的额外空间来完成这个排序。

整体来讲我们要使用三个索引来在数组内进行追踪。

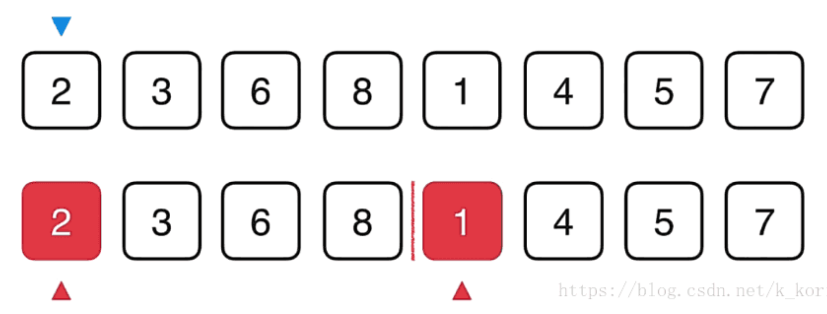
蓝色的箭头表示最终选择的位置，而红色的箭头表示两个数组当前要比较的元素，比如当前是2与1比较，1比2小，所以1放到蓝色的箭头中，蓝色的箭头后移，1的箭头后移。

然后2与4比较，2比4小那么2到蓝色的箭头中，蓝色箭头后移，2后移，继续比较.......

代码

将数组二分为多个子序列 ；
子序列进行排序(注：只有1个元素的序列本身就已经是排序好的序列) ；
排序好的子序列间进行比较与合并；
子序列完全合并为一个有序序列；

int arr[];
int new_arr[];//辅助空间
void merge(int left,int right){
    int mid = (left+right)/2;
    int i=left,j=mid+1,k=0;
    while(i<=mid && j<=rihgt){
        if(arr[i]<arr[j]) new_arr[k++]=s[i++];
        else new_arr[k++]=arr[j++];
    }
    while(i<=mid) new_arr[k++] = arr[i++];
    while(j<=right) new_arr[k++]=arr[j++];
    for(i=left,k=0;i<=right;i++,k++) arr[i]=new_arr[k];
}

void mergesort(int left,int right){
    if(left<right){
        int mid = (left+right)/2;
        mergesort(left,mid);
        mergesort(mid+1,right);
        merg(left,right);
    }
}