数组中的逆序对(不懂系列)
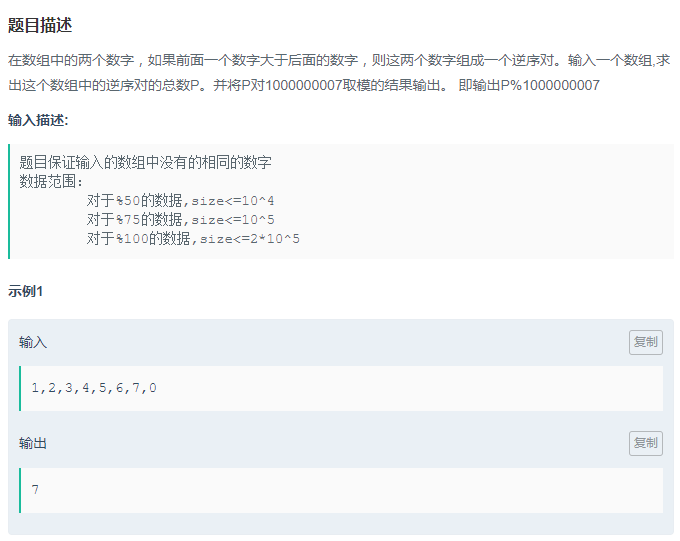
1 class Solution { 2 public: 3 int InversePairs(vector<int> data) { 4 if(data.size() == 0){ 5 return 0; 6 } 7 // 排序的辅助数组 8 vector<int> copy; 9 for(int i = 0; i < data.size(); ++i){ 10 copy.push_back(data[i]); 11 } 12 return InversePairsCore(data, copy, 0, data.size() - 1) % 1000000007; 13 } 14 long InversePairsCore(vector<int> &data, vector<int> ©, int begin, int end){ 15 // 如果指向相同位置,则没有逆序对。 16 if(begin == end){ 17 copy[begin] = data[end]; 18 return 0; 19 } 20 // 求中点 21 int mid = (end + begin) >> 1; 22 // 使data左半段有序,并返回左半段逆序对的数目 23 long leftCount = InversePairsCore(copy, data, begin, mid); 24 // 使data右半段有序,并返回右半段逆序对的数目 25 long rightCount = InversePairsCore(copy, data, mid + 1, end); 26 27 int i = mid; // i初始化为前半段最后一个数字的下标 28 int j = end; // j初始化为后半段最后一个数字的下标 29 int indexcopy = end; // 辅助数组复制的数组的最后一个数字的下标 30 long count = 0; // 计数,逆序对的个数,注意类型 31 32 while(i >= begin && j >= mid + 1){ 33 if(data[i] > data[j]){ 34 copy[indexcopy--] = data[i--]; 35 count += j - mid; 36 } 37 else{ 38 copy[indexcopy--] = data[j--]; 39 } 40 } 41 for(;i >= begin; --i){ 42 copy[indexcopy--] = data[i]; 43 } 44 for(;j >= mid + 1; --j){ 45 copy[indexcopy--] = data[j]; 46 } 47 return leftCount + rightCount + count; 48 } 49 };
归并排序思想
注:
中间交换copy 和 data:
1.在每次的操作中,数值的比较都是采用当前传入函数中第一项,也就是data;比较的结果都存放到copy中;也就意味着此时copy中是经过此次调用的结果。
2.从最底层返回时,进入了(start == end)的情形,data 和 copy 完全没有修改,此时copy和data还是一样的。
3.进入倒数第二层时,程序进入上图26行以后部分,copy是部分排序后的新数组,data是旧数组。注意这里都是传值的调用,数组都是直接修改的。
倒数第二层使用的copy其实是倒数第三层中的data,这就确保了倒数第三层进入26行以后时,数据比较使用的data是最新排序的数组。
4. 倒数第三层将排序的结果存入copy中。程序在倒数第四层进入26行后,使用的data数组为刚刚倒数第三层中的最新排序的copy.
5. 也就是说,在每次程序进入26行时,此时的data是最新的排序结果,copy是次新的结果。
在最后一次进入26行以后时,copy为完整排序后的结果,data是次新的结果。
然而这里第一个类内函数调用第二个函数时,data和copy的顺序没有改变,所以最后结果应该copy是完整排序的结果.data是差一步完成排序的结果。以输入[7,5,6,4], 最后的结果copy[4,5,6,7], data[5,7,4,6].

