LR

一、推导

假设数据服从伯努利二次分布（0-1分布），通过极大化似然函数的方法，运用梯度下降来求解参数，将数据二分类。

1、sigmoid函数

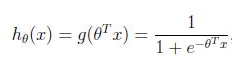
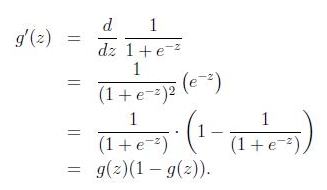
2、假设

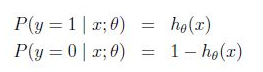
那么概率可以写成：

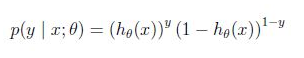
3、使用极大似然估计，那么似然函数是：

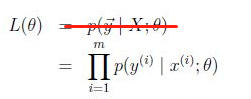
4、对数似然函数

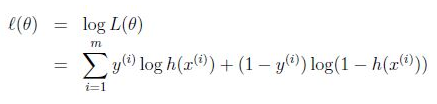
5、接下来使用梯度下降法求解

梯度：

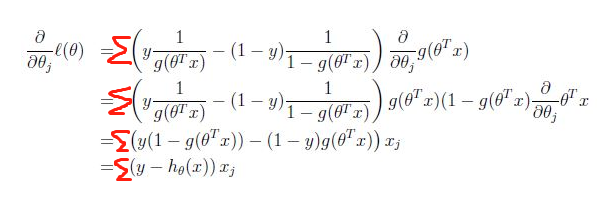
带入梯度下降公式：

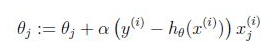
二、优缺点

优点：

• 简单
• 效果也不错
• 速度快
• 占用资源小
• 方便输出调整：通过人工设定阈值

 缺点：

• 准确率不是很高
• 数据不平衡时不好处理，比如说正负样本1000:1，即使把所有样本预测为正，损失函数也很小
• 只能处理线性
• 有时候需要gbdt来筛选特征

三、应用场景

分类、预测概率、某一因素对时间的印象因素分析。

四、适用

特征空间服从伯努利二次分布；

特征空间不大；

线性可分；

五、LR与SVM

LR参数模型，SVM非参数模型。

SVM只考虑在最佳超平面附近的少数支持向量点，二LR不是；

六、LR与线性回归

线性回归用来做预测,LR用来做分类。

线性回归是来拟合函数,LR是来预测函数。

线性回归用最小二乘法来计算参数,LR用最大似然估计来计算参数。

线性回归更容易受到异常值的影响,而LR对异常值有较好的稳定性。

七、LR实现多分类

方法一：最后一层加一个softmax函数，

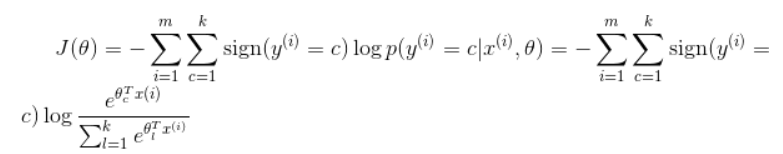
方法二：每一类建立一个二分类器。

八、为什么用MEL

sigmoid函数倒数性质，用对数似然函数求导的时候好求。

九、