局部最优怎么办？

1、使用模拟退火算法SA（Simulate Anneal）

贪心算法是，在求最优解时，从a点开始试探，如果函数值继续减少，那么试探过程继续，到达b点时，试探过程结束（因为无论朝哪个方向努力，结果只会越来越大），因此找到了局部最优b点。

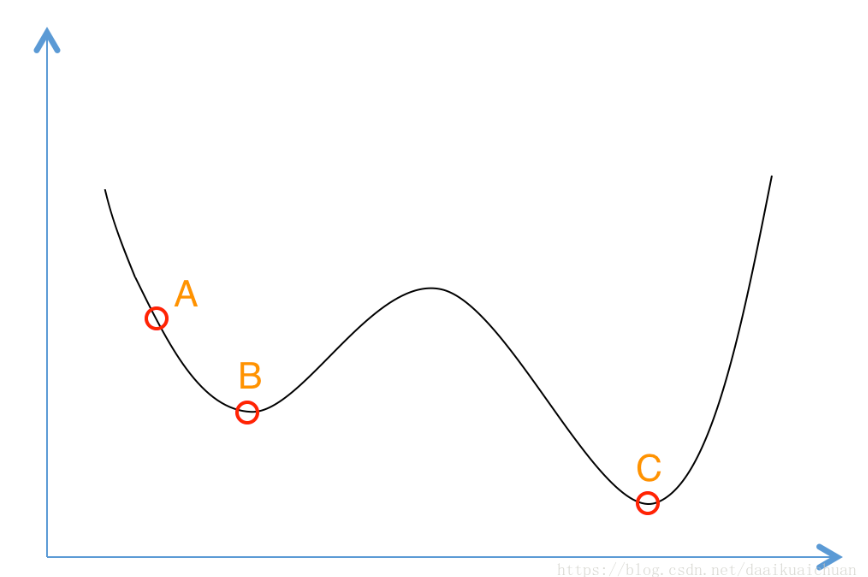
模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）。

过程：

• 若f( Y(i+1) ) <= f( Y(i) ) (即移动后得到更优解)，则总是接受该移动；
• 若f( Y(i+1) ) > f( Y(i) ) (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）相当于上图中，从B移向BC之间的小波峰时，每次右移（即接受一个更糟糕值）的概率在逐渐降低。如果这个坡特别长，那么很有可能最终我们并不会翻过这个坡。如果它不太长，这很有可能会翻过它，这取决于衰减 t 值的设定。

方法2：换个优化方法

局部最优一般是鞍点或者停滞区，就是在某一方向上他是极小值，但是在与它垂直的方向上，却是一个极大值。

但是在这个方向上计算的梯度为0，可能算法就停止迭代了。

所以使用momentum冲量，在遇到停滞区或者鞍点时，靠惯性冲出这个小坑，到真正的大坑里面。算法停止的标准是冲量小于某一个值且梯度小于某一个值，或者指定一个迭代次数就行了。

方法三：调节学习率

对于学习率，采用adagrad、adadelta，自适应学习率。根据历史学习率累计总量来决定当前学习率减小的成都。

adagrad初始学习率要手动指定，adadelta不需要。

adadelta在后期容易在局部最小值附近抖动。

RMSprop是adadelta的一个特例，需要手动设置全局学习率，效果在adagrad 和 adadelta之间。对RNN效果好。