HDU 2256 Problem of Precision 数论矩阵快速幂

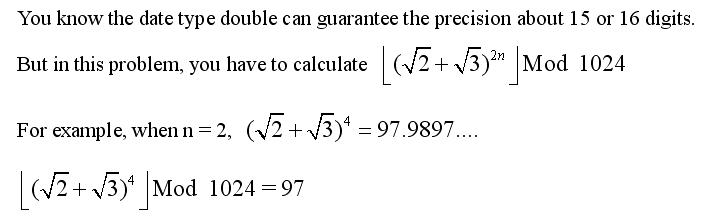
题目要求求出(√2+√3)²ⁿ的整数部分再mod 1024。

(√2+√3)²ⁿ=(5+2√6)ⁿ

如果直接计算，用double存值，当n很大的时候，精度损失会变大，无法得到想要的结果。

我们发现(5+2√6)ⁿ+(5-2√6)ⁿ是一个整数（2√6的奇数次幂总会正负抵消掉），并且(5-2√6)ⁿ是小于1的。所以我们就只需要求出S_(n)-1即可。令

　　A_n=(5+2√6)ⁿ;  B_n=(5-2√6)ⁿ.

　　S_n=A_n+B_n     S_n为整数。

　　S_n*((5+2√6)+(5-2√6))=S_n*10

　　S_n*10=(5+2√6)ⁿ⁺¹+(5-2√6)ⁿ⁺¹+(5+2√6)^n-1+(5-2√6)^n-1

　　S_n*10=S_n+1+S_n-1

　　递推式：S_n=10*S_n-1-S_n-2

然后转化为矩阵快速幂求S_n

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

const int Mod=1024;
const int N=2;
struct Mat
{
    int mat[N][N];
}a;
Mat Multiply(Mat a, Mat b)
{
    Mat c;
    memset(c.mat, 0, sizeof(c.mat));
    for(int k = 0; k < 2; ++k)
        for(int i = 0; i < 2; ++i)
            if(a.mat[i][k])
                for(int j = 0; j < 2; ++j)
                    if(b.mat[k][j])
                        c.mat[i][j] = (c.mat[i][j] +a.mat[i][k] * b.mat[k][j])%Mod;
    return c;
}
Mat QuickPower(Mat a, int k)
{
    Mat c;
    memset(c.mat,0,sizeof(c.mat));
    for(int i = 0; i < 2; ++i)
        c.mat[i][i]=1;
    for(; k; k >>= 1)
    {
        if(k&1) c = Multiply(c,a);
        a = Multiply(a,a);
    }
    return c;
}
void InitMat(Mat &A)
{
    A.mat[0][0]=10; A.mat[0][1]=-1;
    A.mat[1][0]=1;  A.mat[1][1]=0;
}
int main()
{
    //freopen("in.txt","r",stdin);
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        if(n==1)
            printf("9\n");
        else if(n==2)
            printf("97\n");
        else
        {
            InitMat(a);
            a=QuickPower(a,n-2);
            int ans=(a.mat[0][0]*98+a.mat[0][1]*10-1)%1024;  //我们求的是S[n]-1
            while(ans<0) ans+=1024;
            printf("%d\n",ans);
        }
    }
    return 0;
}