信号与系统(二):LTI系统
该部分在前半段的部分手写证明中错将δ写成φ,请见谅,等有空再改过来
LTI系统指线性时不变系统。该系统同时具备线性系统和时不变系统的性质,即齐次性、叠加性和时不变性。
对于一个LTI系统 x(t) -> y(t),可以写成y(t) = x(t) * h(t),即卷积运算(这里和编程语言中的乘号区分)。其中x(t)被称为单位脉冲序列。h(t)被称为单位脉冲响应。
h(t)是LTI系统的唯一标识:如果两个LTI系统的h(n)一样,则两个系统是一样的。
1. 冲激函数
首先定义冲激函数δ(t)和δ[n]。冲激函数具体表现为在t=0处,函数值无限逼近于正无穷,而冲激函数在定义域上的积分是1.冲激函数用图像有两种表示方法:
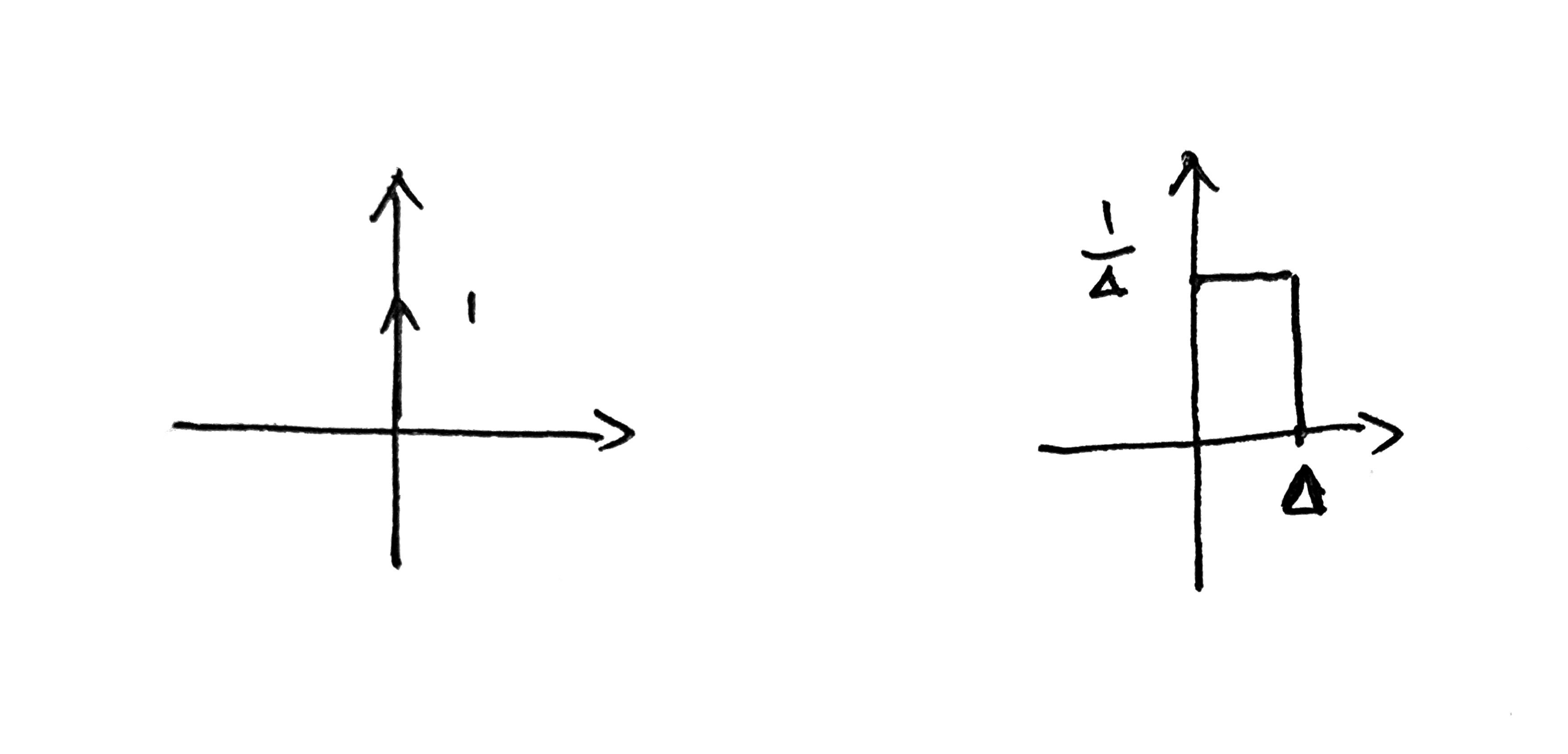
其中左图中的1表示该函数图像与x轴围成的面积(即其在定义域上的积分)为1.一种更好理解的画法是右图,当Δ->0时,1/Δ->+∞,但函数的积分始终是1.
有的书上可以看到另一种定义方法,其实质是一样的,后面会证明。

2. 离散LTI系统的卷积运算
解法一:列表法
- 确定y[n] = x[n] * h[n] 的取值范围:[x[n]的最左边+h[n]的最左边, [x[n]的最右边+h[n]的最右边]
- 列表
例如:对于如下x[n], h[n],
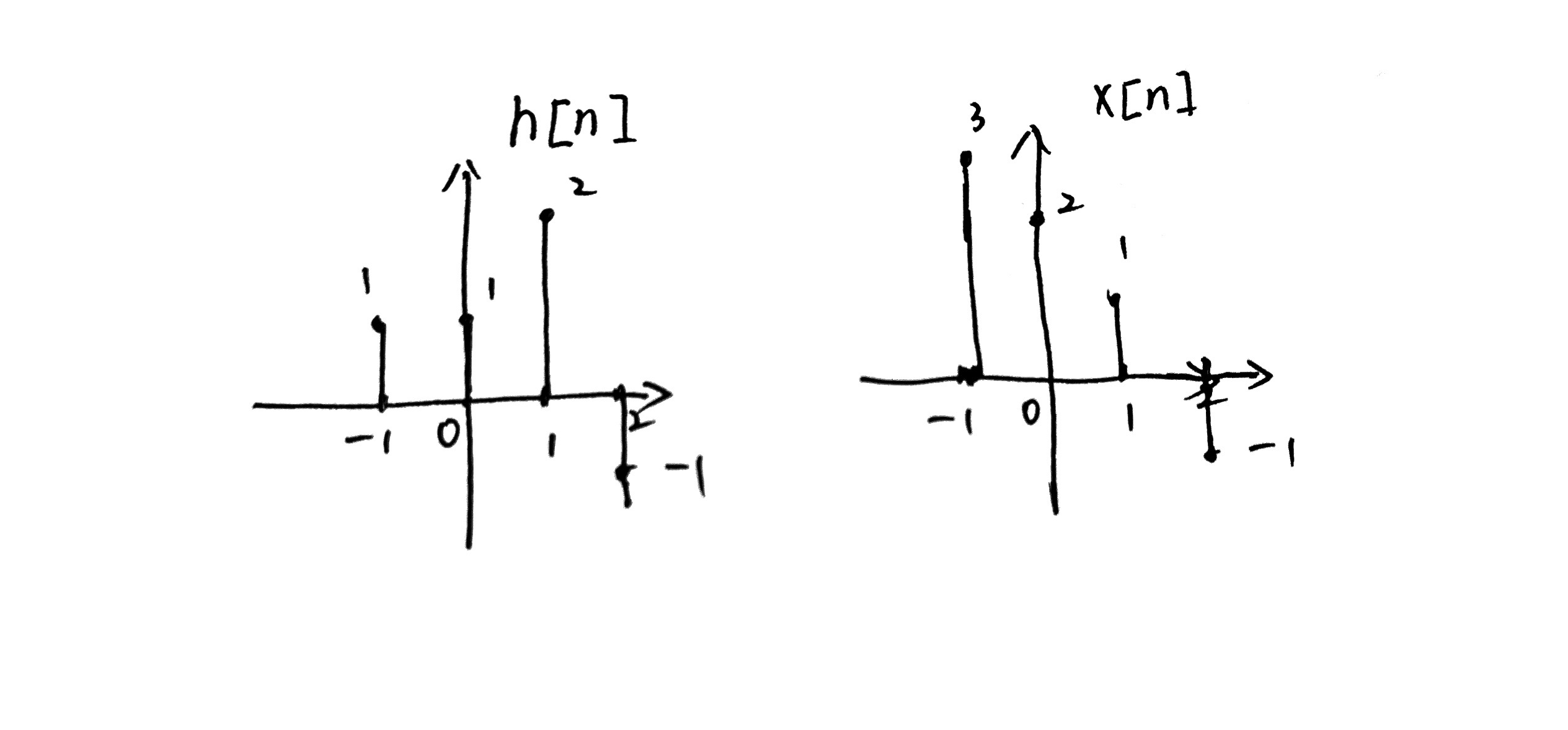
列表:
| x[n]\h[n] | 1 | 1 | 2 | -1 | |||
|---|---|---|---|---|---|---|---|
| 3 | 3 | 3 | 6 | -3 | |||
| 2 | 2 | 2 | 4 | -2 | |||
| 1 | 1 | 1 | 2 | -1 | |||
| -1 | -1 | -1 | -2 | 1 | |||
| 求和 | 3 | 5 | 9 | 1 | -1 | -3 | 1 |
解法二:公式法
卷积公式:
离散卷积公式推导:
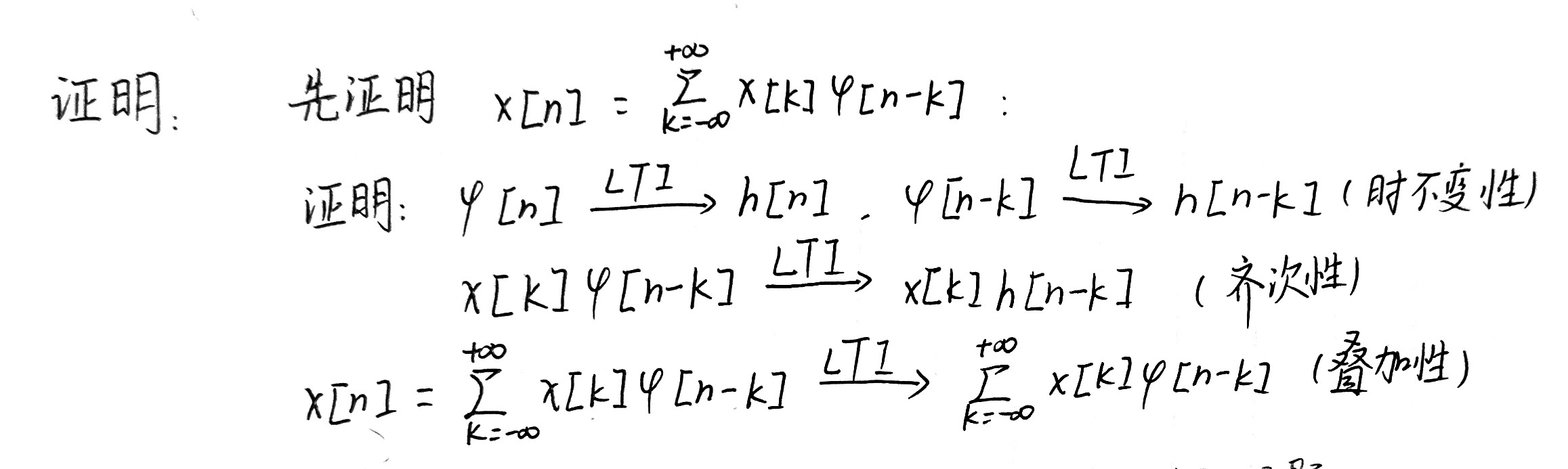
将公式转化为以下形式:
从公式中可以看出计算过程设计四个步骤:
- 确定取值范围
- h[n]反转为h[-n]
- x[n]照抄
- 乘、加、移位
例如,对于上面那道题,先写出h[-n]和x[n]
h[-n]: -1 2 1 1
x[n] : 3 2 1 -1
if t == -2:
-1 2 1 1
3 2 1 -1
y[-2] = 1×3 = 3
if t == -1:
-1 2 1 1
3 2 1 -1
y[-2] = 1×3 + 1×2 = 5
if t == 0:
-1 2 1 1
3 2 1 -1
y[-2] = 6+2+1 = 9
...
if t == 4
-1 2 1 1
3 2 1 -1
y[4] = -1
由此可以求出y[n]的每一项的值。
3. 连续LTI系统的卷积运算
可以构造一个离散的函数来拟合连续的函数。当相邻离散值之间间隔的t->0时,该离散函数将会无限接近于连续函数。我们会发现,这其实就是积分的定义。
连续卷积公式推导:

最终我们可以得到连续卷积的计算公式:
4. 冲激函数δ(t)的性质
性质一
核心:
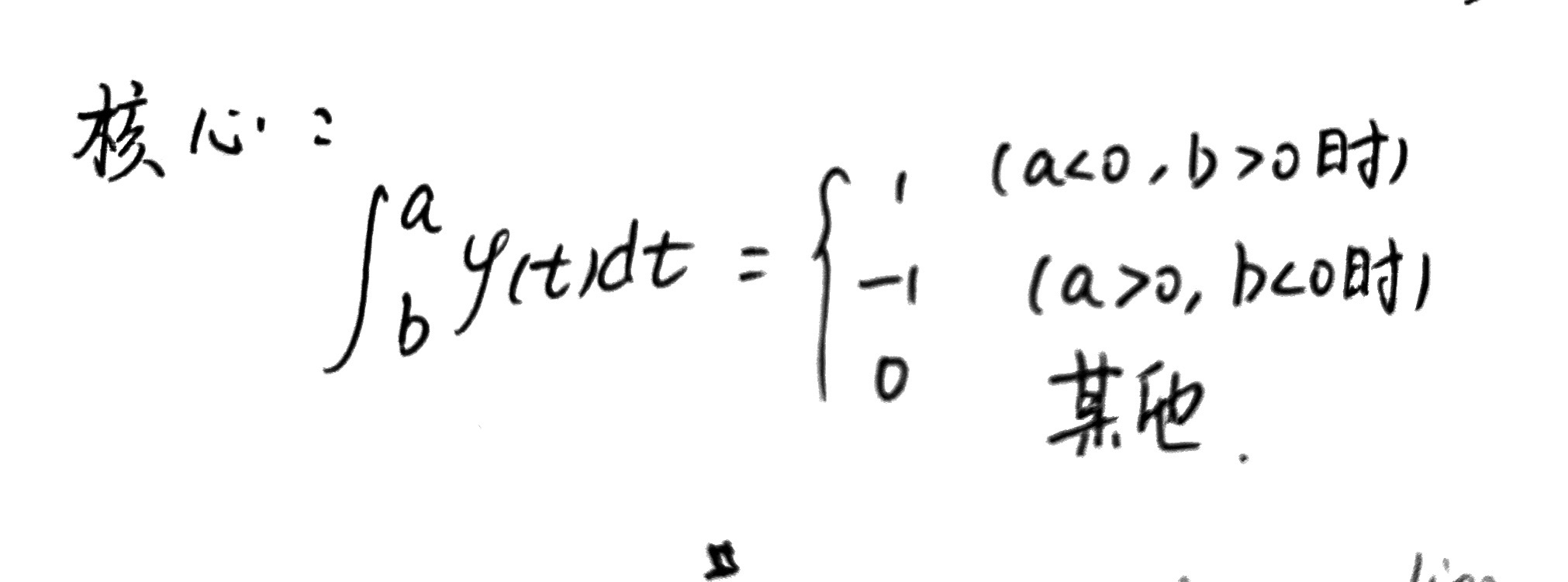
性质二
证明:
性质三
证明:

广义上的性质三
性质四
证明:

广义上的性质四
性质五
定理
若h1(t) = h2(t),则x(t)*h(t) = x(t)*h(t)

这里涉及到勒贝格函数相等的定义和勒贝格积分,将会在“信号与系统(拓展一):勒贝格积分”中详述。
习题
ex. δ(t2-3t+2) = ?
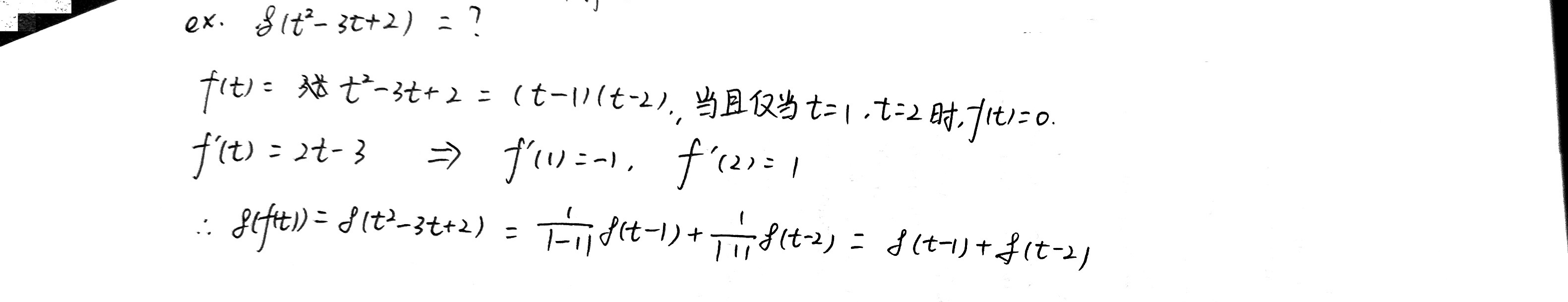
ex. ∫2Π -2Π(1+t) δ(cost)dt = ? δ(cost)=? δ(sint)=?
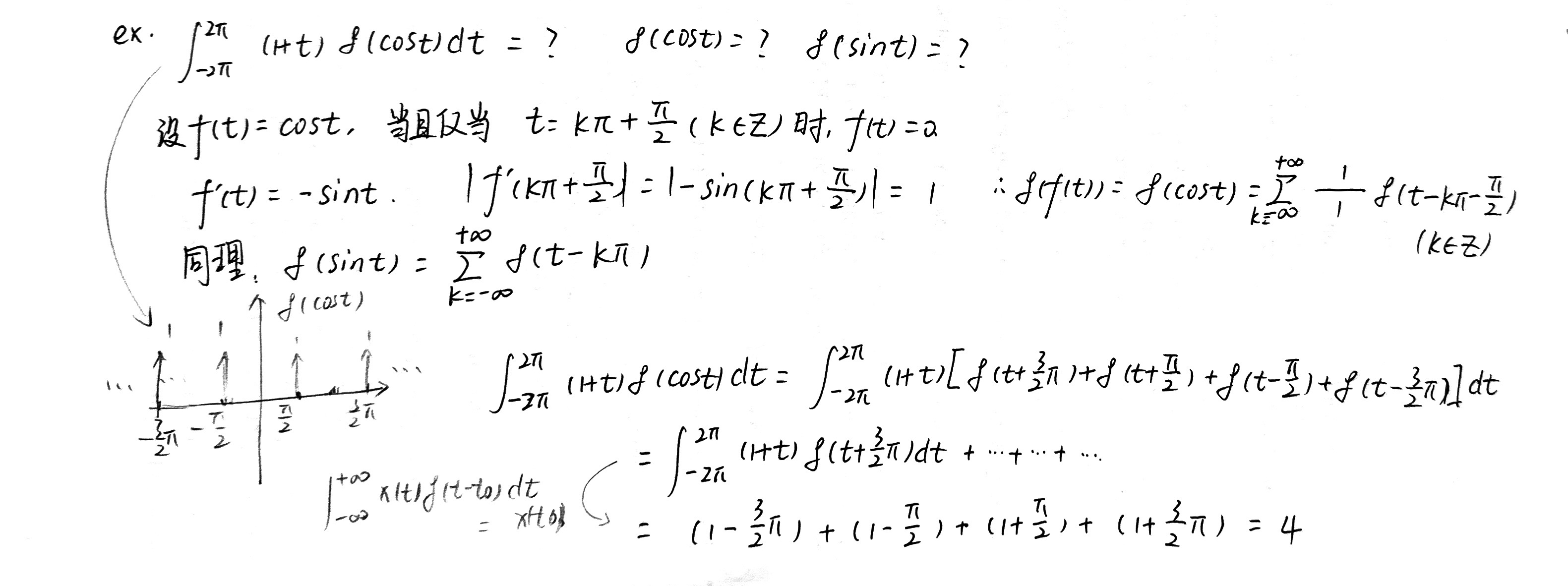
5. 冲激函数δ(t)的多样性
前面提到,冲激函数在不同的书上可能出现两种定义方法,区别在于定义域是[0,Δ]还是[-Δ/2, Δ/2]。利用勒贝格积分,我们可以证明这两个函数其实是一个函数(宽松的限定)。
勒贝格对两个函数相等的定义:要证明f1(t) = f2(t),对于任意函数y(t),有
结合冲激函数的性质二,我们可以得到以下判定:
要证明一个函数f(t)是δ(t),只须证明对于任意函数y(t),有:
此时证明定义域为[-Δ/2, Δ/2]时也是冲激函数,证明:
符合判据,所以按照勒贝格的判定,定义在[-Δ/2, Δ/2]的这个函数也是冲激函数。
6. 连续卷积运算
核心:
两道例题:
用公式直接计算

用画图的方法计算
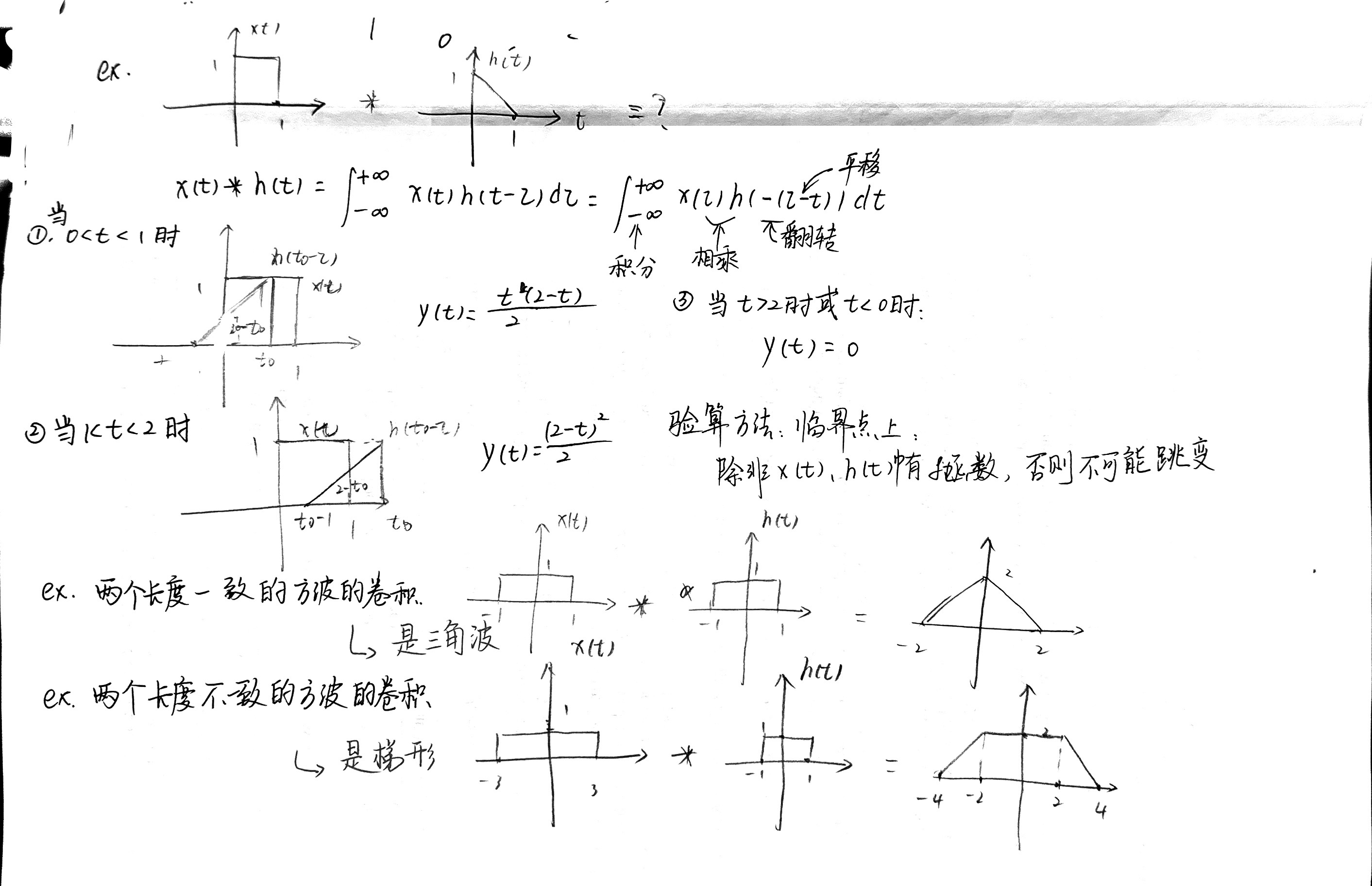
两条定理:
- 两个长度一致的方波的卷积是三角波
- 两个长度不一致的方波的卷积是梯形波
7. 卷积的性质
(1) 交换律
(2) 结合律
证明:

定理:两个LTI系统的串联或并联仍然是LTI系统
(3) 分配律
8. 本章补充知识
1
u(t)是一个特殊的函数,在[-∞, 0]上u(t) = 0,在[0, ∞]上u(t) = 1。
2
3
冲击偶函数的定义:
在x->-0时,δ’(t)->+∞;在x->+0时,δ’(t)->-∞
4
证明:
本文作者:PaB式乌龙茶
本文链接:https://www.cnblogs.com/pab-oolongtea/p/17118234.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步