一、前言
这次呢,我想通过做一些RSA的题来记录一下RSA的各种套路和相关工具的使用,同时呢,能够备份一下我的脚本,害,这脚本写起来是真的伤脑筋。
二、正片
1、一些软件和工具的使用
1.openssl的使用
生成私钥
openssl 生成并输入一个RSA私钥 输出参数 私钥名称 对应的n
openssl genrsa -out private.pem 1024
提取公钥
openssl 处理RSA密钥的格式转换等问题 提取 输出参数 公钥名称
openssl rsa -in private.pem -pubout -out public.pem
Usage: rsa [options] Valid options are: -help Display this summary -inform format Input format, one of DER NET PEM -outform format Output format, one of DER NET PEM PVK -in val Input file -out outfile Output file -pubin Expect a public key in input file -pubout Output a public key -passout val Output file pass phrase source -passin val Input file pass phrase source -RSAPublicKey_in Input is an RSAPublicKey -RSAPublicKey_out Output is an RSAPublicKey -noout Don't print key out -text Print the key in text -modulus Print the RSA key modulus -check Verify key consistency -* Any supported cipher -pvk-strong Enable 'Strong' PVK encoding level (default) -pvk-weak Enable 'Weak' PVK encoding level -pvk-none Don't enforce PVK encoding -engine val Use engine, possibly a hardware device
把public.key丢进kali的openssl进行公钥提取
命令:
openssl rsa -pubin -text -modulus -in public.key
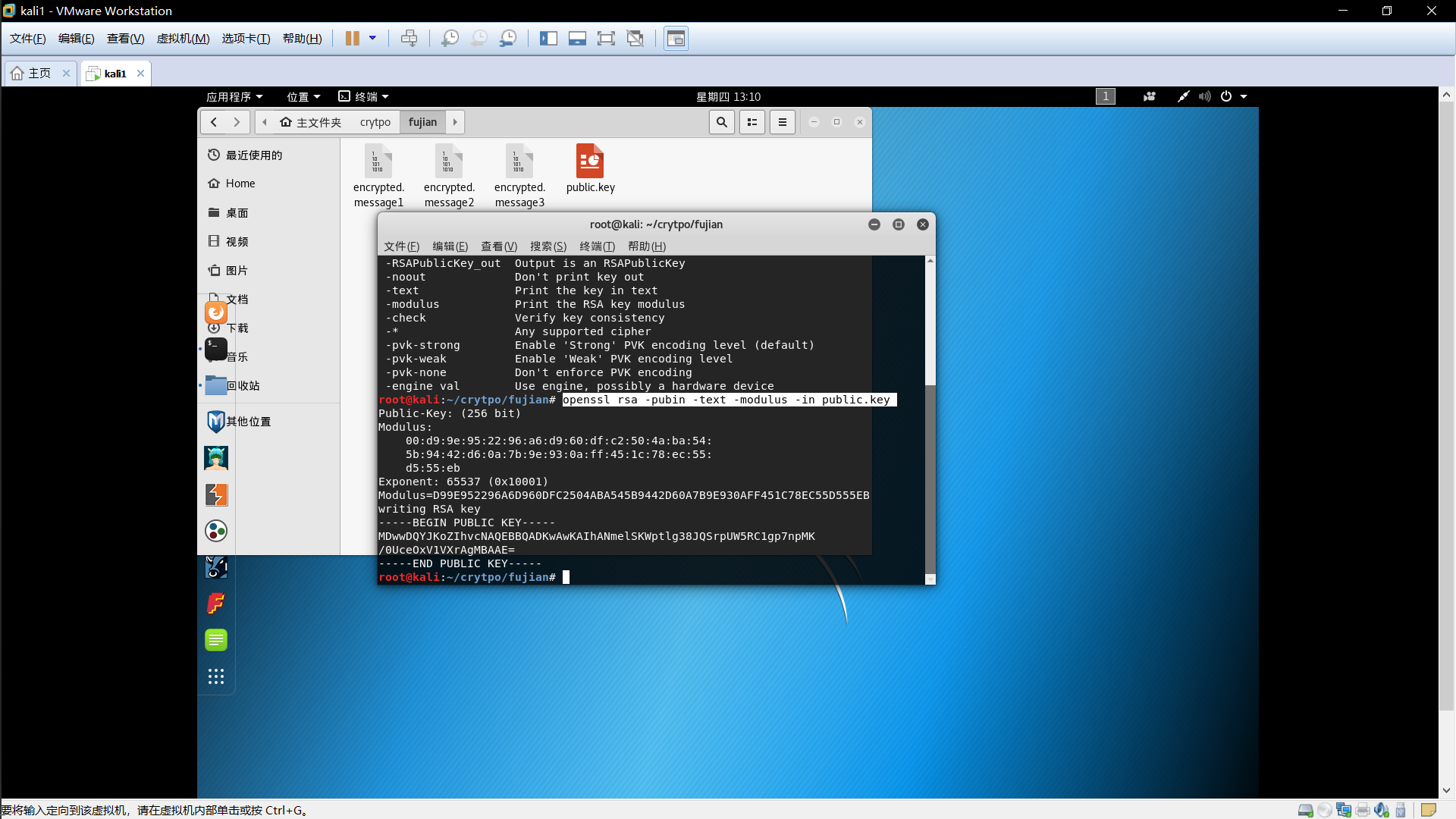
这样就把公钥提出来了,e=65537,n=D99E952296A6D960DFC2504ABA545B9442D60A7B9E930AFF451C78EC55D555EB.
将n转成10进制。
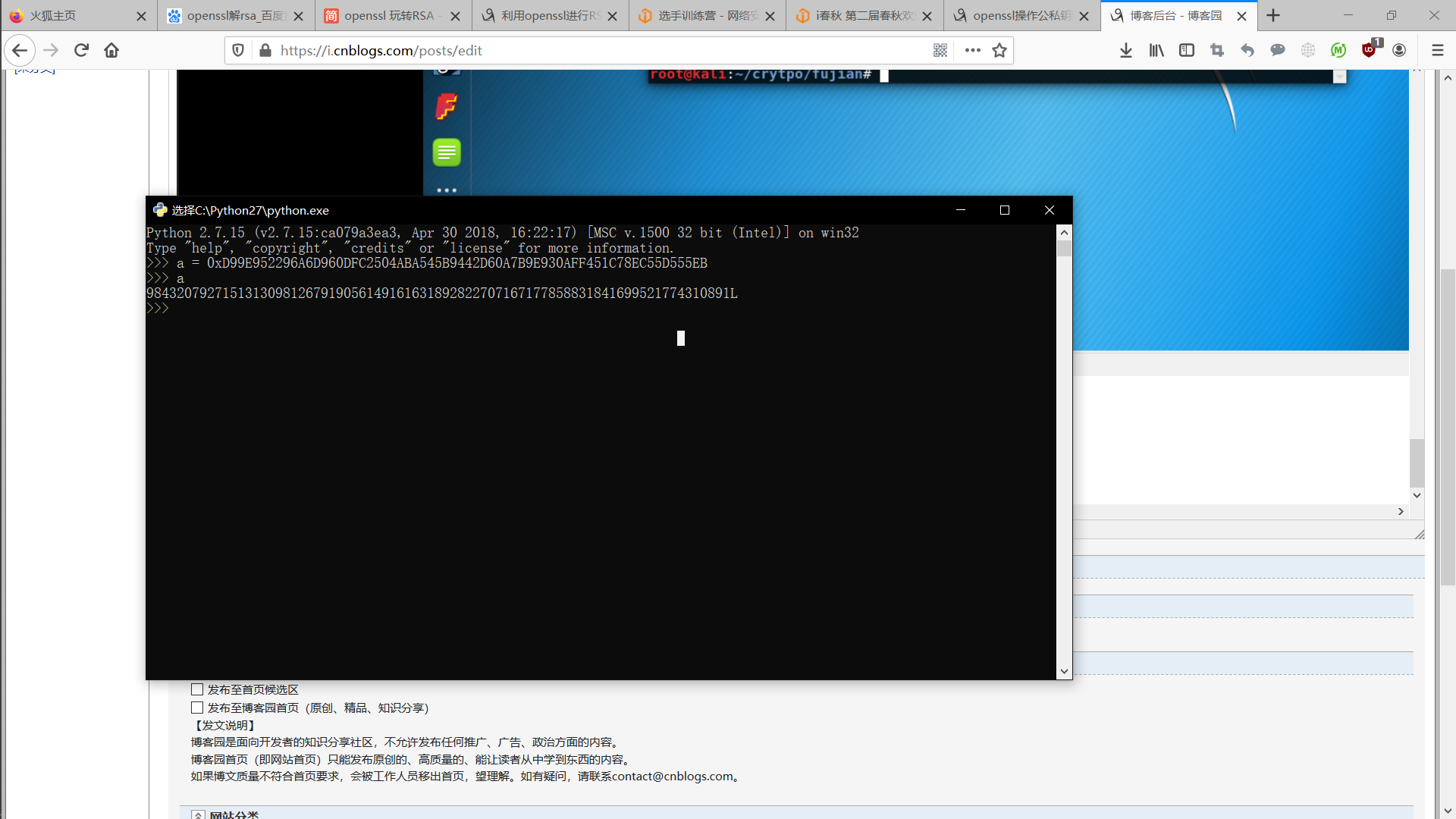
分解n
网址:http://www.factordb.com/index.php
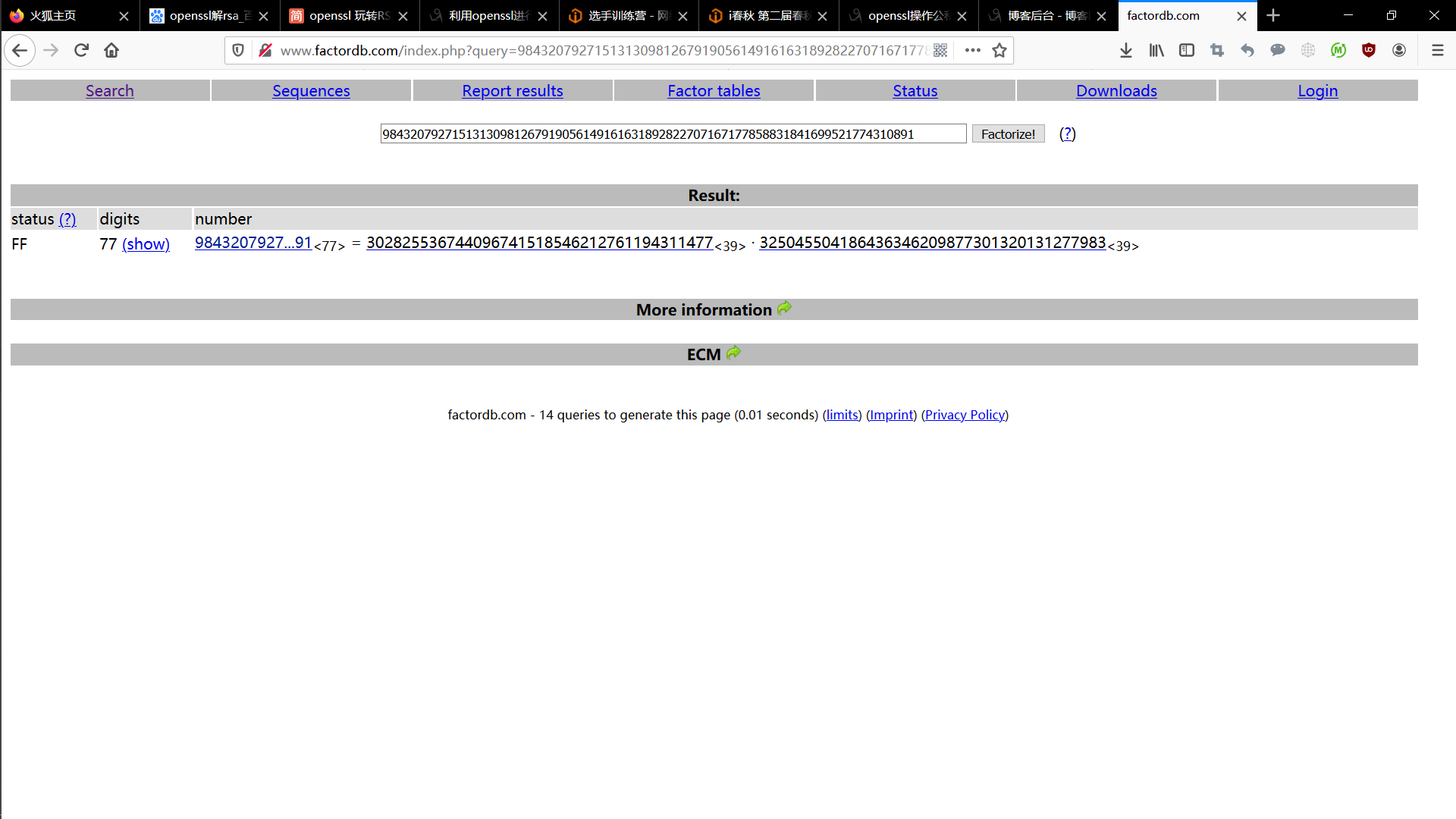
p=302825536744096741518546212761194311477,q=325045504186436346209877301320131277983
然后就是基础的RSA解密
import gmpy2 import rsa p = 302825536744096741518546212761194311477 q = 325045504186436346209877301320131277983 n = 98432079271513130981267919056149161631892822707167177858831841699521774310891 e = 65537 d = int(gmpy2.invert(e , (p-1) * (q-1))) privatekey = rsa.PrivateKey(n , e , d , p , q) #根据已知参数,计算私钥 with open("encrypted.message1" , "rb") as f: print(rsa.decrypt(f.read(), privatekey).decode()) #使用私钥对密文进行解密,并打印 with open("encrypted.message2" , "rb") as f: print(rsa.decrypt(f.read(), privatekey).decode()) with open("encrypted.message3" , "rb") as f: print(rsa.decrypt(f.read(), privatekey).decode())
三、重点题型攻略
1、e=1
IceCTFRSA?
N=0x180be86dc898a3c3a710e52b31de460f8f350610bf63e6b2203c08fddad44601d96eb454a34dab7684589bc32b19eb27cffff8c07179e349ddb62898ae896f8c681796052ae1598bd41f35491175c9b60ae2260d0d4ebac05b4b6f2677a7609c2fe6194fe7b63841cec632e3a2f55d0cb09df08eacea34394ad473577dea5131552b0b30efac31c59087bfe603d2b13bed7d14967bfd489157aa01b14b4e1bd08d9b92ec0c319aeb8fedd535c56770aac95247d116d59cae2f99c3b51f43093fd39c10f93830c1ece75ee37e5fcdc5b174052eccadcadeda2f1b3a4a87184041d5c1a6a0b2eeaa3c3a1227bc27e130e67ac397b375ffe7c873e9b1c649812edcd e=0x1 c=0x4963654354467b66616c6c735f61706172745f736f5f656173696c795f616e645f7265617373656d626c65645f736f5f63727564656c797d
看到分解N的方法行不通。 这时候注意到 e =1。
这时候加密的过程实际为 c = m^e = m ^ 1 = m mod N。
也就是说消息m的数值形式对N取模的余数是密文c。 消息与密文的关系为 m = c + N*k (k=0,1,2,3...)
对明文进行爆破
2、超简单RSA
2017第二届广东省强网杯线上赛RSA1 2 3 | n is 966808932627497190635859236054960349099463975227350564265384373280336699853387254070662881265937565163000758606154308757944030571837175048514574473061401566330836334647176655282619268592560172726526643074499534129878217409046045533656897050117438496357231575999185527675071002803951800635220029015932007465117818739948903750200830856115668691007706836952244842719419452946259275251773298338162389930518838272704908887016474007051397194588396039111216708866214614779627566959335170676055025850932631053641576566165694121420546081043285806783239296799795655191121966377590175780618944910532816988143056757054052679968538901460893571204904394975714081055455240523895653305315517745729334114549756695334171142876080477105070409544777981602152762154610738540163796164295222810243309051503090866674634440359226192530724635477051576515179864461174911975667162597286769079380660782647952944808596310476973939156187472076952935728249061137481887589103973591082872988641958270285169650803792395556363304056290077801453980822097583574309682935697260204862756923865556397686696854239564541407185709940107806536773160263764483443859425726953142964148216209968437587044617613518058779287167853349364533716458676066734216877566181514607693882375533e is 65537c is 168502910088858295634315070244377409556567637139736308082186369003227771936407321783557795624279162162305200436446903976385948677897665466290852769877562167487142385308027341639816401055081820497002018908896202860342391029082581621987305533097386652183849657065952062433988387640990383623264405525144003500286531262674315900537001845043225363148359766771033899680111076181672797077410584747509581932045540801777738548872747597899965366950827505529432483779821158152928899947837196391555666165486441878183288008753561108995715961920472927844877569855940505148843530998878113722830427807926679324241141182238903567682042410145345551889442158895157875798990903715105782682083886461661307063583447696168828687126956147955886493383805513557604179029050981678755054945607866353195793654108403939242723861651919152369923904002966873994811826391080318146260416978499377182540684409790357257490816203138499369634490897553227763563553981246891677613446390134477832143175248992161641698011195968792105201847976082322786623390242470226740685822218140263182024226228692159380557661591633072091945077334191987860262448385123599459647228562137369178069072804498049463136233856337817385977990145571042231795332995523988174895432819872832170029690848 |
分解n
1 2 | p = 31093551302922880999883020803665536616272147022877428745314830867519351013248914244880101094365815998050115415308439610066700139164376274980650005150267949853671653233491784289493988946869396093730966325659249796545878080119206283512342980854475734097108975670778836003822789405498941374798016753689377992355122774401780930185598458240894362246194248623911382284169677595864501475308194644140602272961699230282993020507668939980205079239221924230430230318076991507619960330144745307022538024878444458717587446601559546292026245318907293584609320115374632235270795633933755350928537598242214216674496409625928797450473q = 31093551302922880999883020803665536616272147022877428745314830867519351013248914244880101094365815998050115415308439610066700139164376274980650005150267949853671653233491784289493988946869396093730966325659249796545878080119206283512342980854475734097108975670778836003822789405498941374798016753689377992355122774401780930185598458240894362246194248623911382284169677595864501475308194644140602272961699230282993020507668939980205079239221924230430230318076991507619960330144745307022538024878444458717587446601559546292026245318907293584609320115374632235270795633933755350928537598242214216674496409625928997877221 |
代码如下
# coding=utf-8 import gmpy2 from Crypto.Util.number import * from gmpy2 import iroot,invert n = 966808932627497190635859236054960349099463975227350564265384373280336699853387254070662881265937565163000758606154308757944030571837175048514574473061401566330836334647176655282619268592560172726526643074499534129878217409046045533656897050117438496357231575999185527675071002803951800635220029015932007465117818739948903750200830856115668691007706836952244842719419452946259275251773298338162389930518838272704908887016474007051397194588396039111216708866214614779627566959335170676055025850932631053641576566165694121420546081043285806783239296799795655191121966377590175780618944910532816988143056757054052679968538901460893571204904394975714081055455240523895653305315517745729334114549756695334171142876080477105070409544777981602152762154610738540163796164295222810243309051503090866674634440359226192530724635477051576515179864461174911975667162597286769079380660782647952944808596310476973939156187472076952935728249061137481887589103973591082872988641958270285169650803792395556363304056290077801453980822097583574309682935697260204862756923865556397686696854239564541407185709940107806536773160263764483443859425726953142964148216209968437587044617613518058779287167853349364533716458676066734216877566181514607693882375533 e = 65537 c = 168502910088858295634315070244377409556567637139736308082186369003227771936407321783557795624279162162305200436446903976385948677897665466290852769877562167487142385308027341639816401055081820497002018908896202860342391029082581621987305533097386652183849657065952062433988387640990383623264405525144003500286531262674315900537001845043225363148359766771033899680111076181672797077410584747509581932045540801777738548872747597899965366950827505529432483779821158152928899947837196391555666165486441878183288008753561108995715961920472927844877569855940505148843530998878113722830427807926679324241141182238903567682042410145345551889442158895157875798990903715105782682083886461661307063583447696168828687126956147955886493383805513557604179029050981678755054945607866353195793654108403939242723861651919152369923904002966873994811826391080318146260416978499377182540684409790357257490816203138499369634490897553227763563553981246891677613446390134477832143175248992161641698011195968792105201847976082322786623390242470226740685822218140263182024226228692159380557661591633072091945077334191987860262448385123599459647228562137369178069072804498049463136233856337817385977990145571042231795332995523988174895432819872832170029690848 p = 31093551302922880999883020803665536616272147022877428745314830867519351013248914244880101094365815998050115415308439610066700139164376274980650005150267949853671653233491784289493988946869396093730966325659249796545878080119206283512342980854475734097108975670778836003822789405498941374798016753689377992355122774401780930185598458240894362246194248623911382284169677595864501475308194644140602272961699230282993020507668939980205079239221924230430230318076991507619960330144745307022538024878444458717587446601559546292026245318907293584609320115374632235270795633933755350928537598242214216674496409625928797450473 q = 31093551302922880999883020803665536616272147022877428745314830867519351013248914244880101094365815998050115415308439610066700139164376274980650005150267949853671653233491784289493988946869396093730966325659249796545878080119206283512342980854475734097108975670778836003822789405498941374798016753689377992355122774401780930185598458240894362246194248623911382284169677595864501475308194644140602272961699230282993020507668939980205079239221924230430230318076991507619960330144745307022538024878444458717587446601559546292026245318907293584609320115374632235270795633933755350928537598242214216674496409625928997877221 d = int(gmpy2.invert(e , (p-1) * (q-1))) phi=(p-1)*(q-1) print(phi) d=int(invert(e,phi)) m=pow(c,d,n) print(long_to_bytes(m))





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步