《区间最值操作与历史最值问题》 - 学习笔记
一只高二菜逼在省选前两天发现自己根本不会 segment tree beats ……
3 区间最值操作

直接使用经典做法,在区间中记录最大值,最大值的个数,次大值即可。
证明一下复杂度。首先找一个好看的方法描述一棵线段树,吉老师选择了这样的方法:
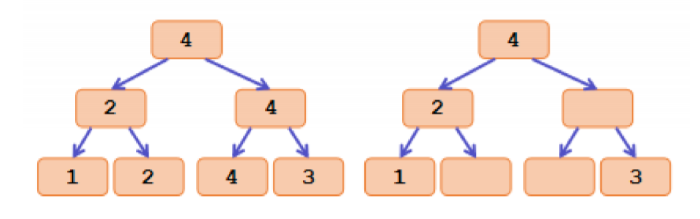
在每个节点维护区间中的最大值作为 tag ,然后把和父亲相等的 tag 删掉。这样区间中的次大值就是子树中的 tag 的最大值。并且显然还满足自己的 tag 严格大于子树中的 tag 。
(在真实的线段树中肯定不会这么写,但两者等价。)
(然后写的东西和论文不太一样,我希望我是对的。)
一次区间操作,会先在线段树上定位到 \(O(\log n)\) 个区间,定位的过程中会把没有完全覆盖的区间的 tag 推到没有 tag 的儿子处。到了对应区间之后更新这里的 tag 。如果发现此时子树中存在更大的 tag 那么就需要暴力 dfs 下去把那些 tag 删掉。
对于没有被完全覆盖的区间,标记下传是为了保留这里的信息(因为儿子并没有存),而它 pushup 的时候可能又会把下面的标记抢过来,相当于标记上传。
定义“标记类”:一次操作给对应区间更新的 tag 为一类,另外如果一个 tag 被祖先抢了过去那么仍然认为它在原来那一类。定义一个标记类的权值为子树中存在这一类标记的点数,定义势能为所有标记类的权值之和。
一次操作会给若干个区间打上同一个标记类的 tag ,显然这个新增标记类的权值是 \(O(\log n)\) (普通线段树复杂度)。
根据定义,一个标记类的 tag 都是相等的。所以暴力 dfs 的时候会把子树中这一类标记全部清空,所以遍历了几个点就让势能减小了多少。
标记下传在一次操作中只会进行 \(O(\log n)\) 次,且只会让势能增加 1 。标记上传是 \(O(1)\) 的,并且不会增加标记类的权值,所以不需要管。
初始势能也是 \(O(n\log n)\) ,所以总复杂度 \(O((n+m)\log n)\) 。

做法和前一题完全一样。继续分析复杂度。
因为吉老师分析不出 \(O((n+m)\log n)\) ,所以直接开始胡乱分析。
不再关心标记类(因为区间加减会使得一个标记类的 tag 不再相等),直接设标记深度和为势函数。一次 pushdown 增加 \(O(\log n)\) 的势能,打一个 tag 也会增加 \(O(\log n)\) 的势能。
胡乱分析就可以搞出 \(O(m\log^2 n)\) 。
注意我们几乎没有利用区间加减的任何性质,任何一个保持子树中 tag 位置不变的操作都可以直接丢进去。
3.1 小结

(这和小结有什么关系)
直接把 min 和 max 的做法合并到一起,分别分析复杂度。它们几乎互不影响,除非在做区间取 min 的时候直接影响到了区间次大值,但是这种情况要么会直接往下递归,要么区间中只有两种值。
然而现在也不能保证标记类的值相等了,所以只能套 \(O(m\log^2 n)\) 的复杂度分析了……
总感觉有很多性质没有用(这题甚至都没有区间加减操作,就只有一个上界和一个下界往中间逼),但是又不会用,像极了我做几何题的样子(((
3.2 将区间最值操作转化为区间加减操作
因为我们的暴力递归操作,所以真正进行的操作只有整体加减和对最值加减。
于是就可以把区间最值的 tag 和整体的 tag 分开维护,好写很多。

整体加减就给 \(B\) 整体加,最值加减就只给最值的位置加。
因为同时有对 max 和 min 的操作,可能有神必细节。

1234 操作都是对两个数组独立的,所以都可以用上面的方法。现在有整体加减、 \(A\) 最值加减、 \(B\) 最值加减,所以我们需要知道一个位置的 \(A,B\) 是否是最值。所以要维护 4 种信息。

最大值单独维护,非最大值差分。合并两个区间的时候可能一边的最大值变成了整体的非最大值,不过差分并不关心序列的顺序具体是怎样,所以只需要把它接在序列末尾即可。
如果是更加依赖于序列顺序的询问可能就死掉了。
4 历史最值问题
4.2 可以用懒标记处理的问题

烦死了(
如果没有区间赋值操作那还比较简单,只需要维护区间加标记和区间加的历史最值标记。一旦这个区间被赋值了,那么以前的区间加标记就废了,需要维护赋值前后的区间加的历史最值,和当前是什么值。

因为有了神必 \(\max(A_i-x,0)\) 操作,区间中每个值经历的事情可能不太一样。维护 tag \((a,b)\) 表示先加 \(a\) 再和 \(b\) 取 \(\max\) 。那么前三种操作都可以直接用这个 tag 表示。
还是要维护历史 tag 的最大值,相当于把两个分段函数的每个位置取 \(\max\) 。发现它的形式竟然没有变化,于是做完了。复杂度 \(O(m\log n)\) 。
这东西是不是也可以区间询问啊?
好像也可以把 1 操作强行转成区间取 \(\max\) ,然后套吉老师线段树。

单点修改,区间和的历史最值。
因为点之间的时间并不独立,所以维护每个位置的历史最值对这题并没有什么用。离线下来,把询问看做点,那么就变成二维前缀加,单点历史最值。
可以 kd tree 做。复杂度 \(O(m\sqrt n)\) 。
4.3 无法用懒标记处理的单点问题
某些区间查询也被称为单点问题,是因为历史最小值的区间最小值和单点并无太大区别。

看到区间取 \(\max\) 就知道这题和吉老师或多或少有点联系。
直接把 1 操作变成给最小值加正数,然后把最值和非最值分开维护,就做完了。
可以类似例 8 维护分段函数吗?但是此时不是历史最大值而是历史最小值,与 \(\max(A_i,x)\) 方向相反,所以合并分段函数的时候无法维持以前的形式。
4.4 无区间最值操作的区间问题
区间加减,维护区间历史最值和/历史版本和。
4.4.1 历史最小值
最小值的和,与最小值的最小值,本质区别在哪里?
在之前,我们在一个节点记录了两个 tag :当前的加法标记&历史最小的加法标记。子树中记录的 历史最小值&当前最小值 其实是仅仅考虑子树中的 tag 之后得到的,我们还需要把它们和这个位置的 tag 合并。
但是因为以前只考虑最小值,所以维护两个值并没有带来什么困扰。
现在要求和,那我们不可能维护每个位置的 历史最小值&当前最小值 ,于是就死掉了。需要寻找新的方法。
注意到当前值一定大于等于历史最小值,只有一次操作减过头的时候才会更新历史最小值。
设 \(C_i=A_i-B_i\) 表示这个位置再减多少才能到达历史最小值,那么一次区间加 \(x\) 就等价于 \(\max(C_i+x,0)\) 。
然后区间和就是对 \(C\) 的区间和了。
4.4.2 历史版本和
因为一次操作未覆盖的部分也需要更新历史版本和,所以考虑设 \(B_i=tA_i+C_i\) ,这里 \(t\) 表示现在是第几次操作, \(C_i\) 就表示与当前的 \(A\) 的偏移量。
容易发现一次操作就是对 \(C\) 的区间加减。
4.5 有区间最值操作的区间问题
根据套路,区间最值操作全部变成对最值的加减操作。然后可能该怎么做就还是怎么做(
真的吗?我们发现无区间最值操作的历史最小值经过转化之后已经变成区间最值操作了,那么再套上区间最值操作之后会变成什么呢?

把 \(B_i\) 的和转化为 \(A,C\) 的区间和。 \(A\) 好做,所以考虑 \(C\) 怎么做。
关于 \(C\) 有两种操作:区间加 \(C_i:=\max(C_i+x,0)\) ,或是给区间中 \(A\) 的最小值的位置加正数。
那就分别维护区间中非 \(A\) 最小值位置和最小值位置的 \(C\) 的最小值、最小值个数、次小值个数,然后直接冲。
(这么一道题要维护多少个 tag 啊……)
冲也冲了,过也过了(?),但是复杂度是啥?
第一种操作只有 \(O(m)\) 种,而第二种操作因为是加正数所以没有取 \(\max\) 操作,对复杂度分析没有太大影响。
但是问题在于 \(A\) 中的最小值的位置在变,所以看起来不是很容易直接分析两种 \(C\) 中的 tag 个数?
复杂度分析看不懂了,跑了。可能只要带上信仰就没有什么是不能冲的(
最后放上洛谷【模板】线段树 3 的代码(常数太大 T 掉了):
using namespace my_std;
int n,m;
ll a[sz];
struct Tag{ll add,pre;Tag(ll A=0,ll P=0){add=A,pre=P;}};
struct Info{int c;ll sum,mx,hmx;Info(int C=0,ll S=0,ll X=-1e17,ll hX=-1e17){c=C,sum=S,mx=X,hmx=hX;}};
Tag merge(Tag x,Tag y){return Tag(x.add+y.add,max(x.pre,x.add+y.pre));}
Info merge(Info x,Tag y){return Info(x.c,x.sum+y.add*x.c,x.mx+y.add,max(x.hmx,x.mx+y.pre));}
Info merge(Info x,Info y){return Info(x.c+y.c,x.sum+y.sum,max(x.mx,y.mx),max(x.hmx,y.hmx));}
Tag tg[sz<<2][2]; Info tr[sz<<2][2];
#define ls k<<1
#define rs k<<1|1
#define lson ls,l,mid
#define rson rs,mid+1,r
void PutTag(int k,const Tag *t){rep(i,0,1) tg[k][i]=merge(tg[k][i],t[i]),tr[k][i]=merge(tr[k][i],t[i]);}
void pushdown(int k)
{
tg[0][0]=tg[0][1]=tg[k][0];
if (tr[ls][1].mx==tr[k][1].mx-tg[k][1].add) PutTag(ls,tg[k]); else PutTag(ls,tg[0]);
if (tr[rs][1].mx==tr[k][1].mx-tg[k][1].add) PutTag(rs,tg[k]); else PutTag(rs,tg[0]);
rep(i,0,1) tg[k][i]=Tag();
}
void pushup(int k)
{
Info L[2]={tr[ls][0],tr[ls][1]},R[2]={tr[rs][0],tr[rs][1]};
int lmx=L[1].mx,rmx=R[1].mx; if (lmx<rmx) swap(lmx,rmx),swap(L,R);
if (lmx==rmx) return tr[k][0]=merge(L[0],R[0]),tr[k][1]=merge(L[1],R[1]),void();
tr[k][1]=L[1]; tr[k][0]=merge(merge(R[0],R[1]),L[0]);
}
void build(int k,int l,int r)
{
if (l==r) return tr[k][1]=Info(1,a[l],a[l],a[l]),tr[k][0]=Info(0,0,-1e17,-1e17),void();
int mid=(l+r)>>1;
build(lson),build(rson);
pushup(k);
}
void add(int k,int l,int r,int x,int y,ll w)
{
if (x<=l&&r<=y) return tg[0][0]=tg[0][1]=Tag(w,max(0ll,w)),PutTag(k,tg[0]),void();
int mid=(l+r)>>1; pushdown(k);
if (x<=mid) add(lson,x,y,w);
if (y>mid) add(rson,x,y,w);
pushup(k);
}
void mdf(int k,int l,int r,int x,int y,ll w)
{
if (tr[k][1].mx<=w) return;
int mid=(l+r)>>1; if (l!=r) pushdown(k);
if (x<=l&&r<=y)
{
if (tr[k][0].mx<w) return tg[0][0]=Tag(),tg[0][1]=Tag(w-tr[k][1].mx,0),PutTag(k,tg[0]);
mdf(lson,x,y,w),mdf(rson,x,y,w),pushup(k); return;
}
if (x<=mid) mdf(lson,x,y,w); if (y>mid) mdf(rson,x,y,w);
pushup(k);
}
Info query(int k,int l,int r,int x,int y)
{
if (x<=l&&r<=y) return merge(tr[k][0],tr[k][1]);
int mid=(l+r)>>1; pushdown(k); Info res;
if (x<=mid) res=merge(res,query(lson,x,y));
if (y>mid) res=merge(res,query(rson,x,y));
return res;
}
int main()
{
file();
read(n,m);
rep(i,1,n) read(a[i]);
build(1,1,n);
while (m--)
{
int tp,l,r,v;
read(tp,l,r);
if (tp==1) read(v),add(1,1,n,l,r,v);
else if (tp==2) read(v),mdf(1,1,n,l,r,v);
else
{
auto ans=query(1,1,n,l,r);
printf("%lld\n",(tp==3?ans.sum:(tp==4?ans.mx:ans.hmx)));
}
}
return 0;
}

