《浅谈函数最值的动态维护》 - 学习笔记
EI 队长不务正业
又是一个(对于我来说)理性愉悦的东西,大概几年之内(或者这辈子?)都不会写这东西的代码……
1 概述
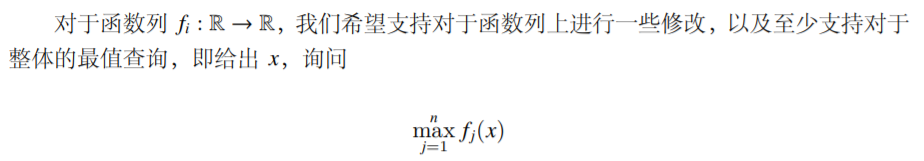
自然的想法是维护这些函数取 \(\max\) 之后得到的分段函数,但这就带来一个问题:分段函数最多能分多少段。
只考虑任意两个函数,如果段数不超过 \(s+1\) ,那么总的分段函数的段数也会有一个比较紧的界。
考虑分段函数每一段属于哪个函数,设为 \(\{a_i\}_{i=0}^m\) 。如果存在 \(x,y\) 使得 \(a\) 中存在长度超过 \(s+1\) 的 \(x,y\) 交替子序列,那就与 \(\max(f_x,f_y)\) 段数不超过 \(s+1\) 矛盾。
于是引入
1.1 Davenport-Schinzel 序列

那么段数的上界就和 \(DS(n,s)\) 的长度有关。
有一个牛逼定理:

于是我们惊喜地发现,段数竟然几乎是线性的。
1.2 DS 序列与问题的联系

为什么 \(s\) 次分段函数的阶是 \(s+2\) 呢?如果定义域无交那么显然只有 2(还是 3 ?)段,否则可能在两者的定义域中已经获得了 \(s\) 个交点,而在边界还会获得两个。
2 函数集合维护
有了上面那个结论之后这里显得比较简单。
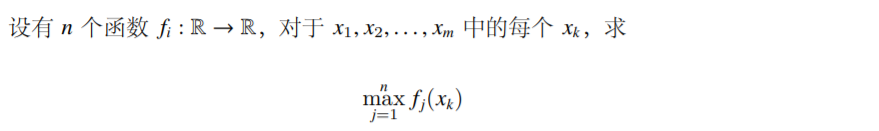
如果函数初始给定,那么直接分治合并所有函数,然后询问的时候二分 \(x\) 在哪一段即可(当然如果可以离线就没必要二分了)。预处理复杂度 \(O(\lambda_s(n)\log n)\) ,询问复杂度 \(O(m\log n)\) 。
如果是一边添加函数一边询问:用经典的二进制分组算法(也就是不完全的分治)处理修改,但询问要在 \(O(\log n)\) 个分段函数上二分,复杂度变为 \(O(m\log^2 n)\) 。
但是容易发现可以用分散层叠来优化二分的过程,在新合并出一个 \(2^k\) 的段时把 \(2^{k},2^{k-1},\cdots,1\) 的分散层叠重构,而重构的复杂度并不是瓶颈。于是复杂度仍然是 \(O(m\log n)\) 。
2.3 应用
2.3.1 维护分段一次函数最值
直接做就行了。
2.3.2 动态规划问题
令 \(f_j(x_i)=a_j+w_{j,i}\) ,如果 \(f_j,f_k\) 交替阶数较低,那就可能可以大力维护分段函数。
通常有两类做法:直接发现 \(f_j\) 是关于 \(x_i\) 的一次函数,或者发现有决策单调性。
如果是一次函数那就直接做,否则决策单调性一般会满足四边形不等式,就有
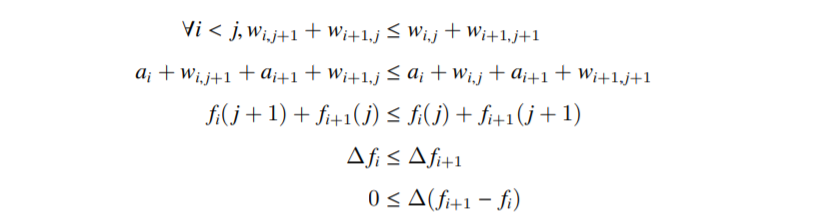
也就是 \(f_{i+1}-f_i\) 单调递增,所以 \(\max(f_i,f_{i+1})\) 在 \((i+1,n]\) 上阶为 1 ,所以 \(i<i_0\) 的函数取 \(\max\) 在 \([i_0,n]\) 上是 \(s=1\) 阶交替。
怎么求分段点就是另外一回事了……?
3 询问点单调递增

3.1 Kinetic Tournament 树
用线段树维护区间中对于当前 \(x\) 取到最大值的函数是哪个,而 \(x\) 变化的时候暴力修改。
每个点的分段个数是 \(\lambda_s(n)\) ,再带上 \(\log n\) 层,再加上修改的时候是暴力从根节点往下 dfs 修改,所以复杂度 \(O(\lambda_s(n)\log^2 n+q)\) 。
3.2 带修改函数序列最值问题
现在可以支持单点修改函数序列。
由于 \(x\) 单调递增,所以一个位置仍然可以看做只有一个函数,只不过这个函数分段。于是复杂度变为 \(O(\lambda_{s+2}(n+m)\log^2 n+q)\) 。
实现的时候当然没有必要关心函数具体怎么分段,修改的时候暴力即可(吧)。所以该在线还是在线。
4 线性情况的扩展
一次函数比较优美,因为如果只有 \(x\) 单调递增的话那么一定是从斜率较小的函数切换为斜率较大的函数。
4.1 包含两类区间修改的序列最值问题

另外还要求 \(x>0\) 。为了方便,再加上 \(k_i,b_i,c>0\) 。
类似于每个位置有一个函数 \(k_ix+b_i\) ,一操作让区间的 \(x\) 增加,二操作看起来比较迷惑,但是被二操作完全覆盖的区间中 \(k,b\) 的大小关系都没有变化,并且好像可以看做 \(x\) 也没有变化?
考虑 \(k_1x+b_1\) 和 \(k_2x+b_2\) ,且 \(b_1>b_2,k_1<k_2\) ,在同时经过二操作之后会发生什么。原来是还需要 \(x\) 增加 \({b_1-b_2\over k_2-k_1}\) 才会使得大小关系改变,而现在竟然完全没有变化。
于是有这么一个做法:线段树维护区间的 \(x,k,b\) 发生了什么变化,以及最大值在哪里取到,以及 \(x\) 再整体增加多少就会使得最大值切换。
一操作时如果没有切换最大值那就无事发生,否则递归下去换;二操作一定不会切换最大值,也不会改变“还要多久才切换”。而 pushup 是简单的。
唯一的问题是一操作中的“递归下去换”,这个复杂度是什么。
4.1.1 复杂度分析
如前所说,切换最大值的时候一定是从斜率小的换成斜率大的。

那么一次对 \(v\) 的切换会使得 \(\Phi\) 减小 \(d(v)\) ,但同时又可能增加 \(d(fa_v)\) ,所以至少减小 1 。
两种操作会带来什么呢?只有被碰到的节点可能会被丢进 \(\mathcal {P}\) 中,只会碰到 \(O(\log n)\) 个点,所以只会增加 \(O(\log^2 n)\) 的势能。
初始还有 \(O(n\log n)\) 的势能。
所以总复杂度 \(O(n\log^2 n+m\log^3 n+q\log n)\) 。
4.1.2 特殊情况
“区间增加公差为正的等差数列”,即保证 \(k_i\) 单调递增。
那么切换就只能从左儿子切换到右儿子。另外,对于 \(x\) ,如果它子树中的 \(\max\) 已经在右儿子了,那么打 \(tag\) 的时候即使 \(ls\) 被切换了, \(x\) 也不会被切换,因为右边加的比左边多。
所以可以直接设 \(\Phi\) 为“\(\max\) 位于左子树”的点数,比上面少一个 \(\log\) ,复杂度 \(O(n\log n+m\log^2 n+q\log n)\) 。
4.2 例题

于是获得了好多个 $\log $(

乱做?
4.2.1 最大连续子段和
区间加正数,区间最大子段和。
于是要维护 \(sum,lmax,rmax,totmax\) 。它们满足

全都是关于区间加的一次函数。
如何构造一个神奇的势函数,使得切换一定会消耗势能呢?显然还是应该和“斜率比自己选的直线的斜率大的个数”有关。要考虑到给自己切换的时候可能也会影响父亲。
当 \(lmax\) 切换,可能会使得自己的斜率比父亲的 \(lmax,totmax\) 大; \(rmax\) 同理;\(totmax\) 则只会使得自己的斜率比父亲的 \(totmax\) 大。所以要求 \(l_d>l_{d-1}+t_{d-1},r\cdots,t_d>t_{d-1}\) 。于是可以令 \(t_d=d,l_d={d(d-1)\over 2}\) 。

初始势能:给 \(lmax\) 的势能贡献 \(O(n\log^2 n)\) ,给 \(totmax\) 的势能贡献 \(O(n\log n)\) 。
一次修改:给 \(lmax\) 的势能贡献 \(O(\log^3 n)\) ,给 \(totmax\) 的势能贡献 \(O(\log^2 n)\) 。
于是分析出了复杂度 \(O(n\log^3 n+m\log^4 n+q\log n)\) (切换一次还会乘上额外的 \(O(\log n)\) )。
不过注意到 \(lmax\) 的转移点一定是单调地从左往右,所以 \(lmax,rmax\) 的总切换次数其实仅仅是 \(O(n\log n)\) ,贡献到 \(totmax\) 的势能上就是 \(O(n\log^2 n)\) ,然后再把 \(totmax\) 的复杂度分析抄过来,就得到 \(O((n+m)\log^3 n+q\log n)\) 。
看着还行
如果没有“转移点单调往右”的性质那就只能用上面那个复杂度分析了。
4.2.2 henry_y 的数列

逐渐阴间。
区间加二次函数?换成把 \(i,i^2\) 看做系数, \((a,b)\) 看做变量。因为 \(i,i^2\) 单调递增,而 \(a,b\ge 0\) ,所以区间打 \(tag\) 时最小值位置一定是从右往左走。
什么时候会切换呢?假设左子树 \(\min\) 在 \(A_i\) ,右子树在 \(A_j\) ,且 \(A_j<A_i\) ,那么
即 \((a,b)\) 走到某个半平面内的时候才会切换。
这就比较麻烦了,切换的条件从一维变成二维的了。
头铁,直接维护子树中的半平面交。注意到直线斜率 \(i+j\) 满足 \(ls< x< rs\) ,所以可以直接可持久化平衡树维护半平面交,合并的时候二分。
另外,仍然注意到右边加的比左边多,所以可以令 \(\Phi\) 为 “\(\min\) 在右子树取到的点数” ,省一个 $\log $ (?)
复杂度 \(O((n+m\log n)\log^2 n+q\log n)\) 。

