《浅谈拟阵的一些拓展及其应用》 - 学习笔记
系统地学习一下。但 是 为 什 么 我 要 啃 证 明 过 程 啊
前几节
前面几节直接跳了,只写一些容易忘或是曾经不是很理解的东西。
环:极小非独立集。注意环删掉一个元素之后是独立集但不一定是基,所以环的大小可以不同(废话,看图拟阵不就看出来了)。
匹配拟阵:不是定了几条边必须要选,而是定了几个点必须要被匹配。
基交换定理:两个基 \(A,B\) ,从 \(A\) 删掉 \(A\backslash B\) 的一个元素之后必然可以补一个 \(B\) 里的元素。虽然是废话但好像比较有用。
推论 2.4 :如果存在环 \(X\ne Y\) 且 \(e\in X\cap Y\) ,那么 \(X\cup Y-\{e\}\) 不是独立集。显然 \(X,Y\) 不存在子集关系,所以包含 \(X\cap Y\) 的最大独立集至少删了两个点。现在 \(X\cup Y-\{e\}\) 能把它补成只删一个点,这显然不可能。
推论 2.5 :一个基加上一个元素得到的集合中包含唯一一个环。如果有两个不同的环 \(C_1,C_2\) ,那么显然有 \(e\in C_1\cap C_2\) ,所以 \(C_1\cup C_2-\{e\}\) 不是独立集,矛盾。
秩函数的次模性: \(\forall A,B\subseteq S,r(A\cup B)+r(A\cap B)\le r(A)+r(B)\) 。这是因为从 \(A\cap B\) 里的最大独立集可以扩展出 \(A\cup B\) 的最大独立集,然后分配一下就得到了 \(A,B\) 里分别一个独立集,但不一定是最大的。
由秩函数定义拟阵:遗传性很显然。交换性可以考虑 \(|A|<|B|\) 且 \(A\cup \{b_i\}\) 都不是独立集,那么可以归纳法,假设 \(r(A\cup \{b_1,\cdots,b_n\})=r(A\cup \{b_{n+1}\})=|A|\) ,那么直接使用次模性得到 \(r(A\cup \{b_1,\cdots,b_{n+1}\})=r(A)=|A|\) ,最终可以推到 \(r(A\cup B)=r(A)<r(B)\) 得到矛盾。
拟阵上的最优化直接跳了。
4 一些补充定义
4.1 对偶拟阵
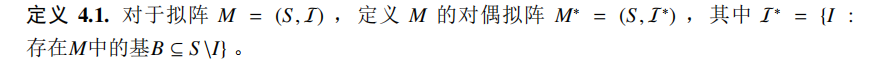
对偶拟阵的独立集的意义是,从 \(S\) 中删掉 \(I\) 后,还需要存在一个基。
而它的秩函数的意义是:可以保留 \(I\) 中的多少个元素,得到 \(I'\) ,使得从 \(S\) 中删掉 \(I'\) 后仍然存在独立集。而不是 \(S\) 删掉 \(I\) 之后的最大独立集大小。当然,可以看出这两者是有直接关系的,比如观察下面的秩函数。
然后求一手新的秩函数:
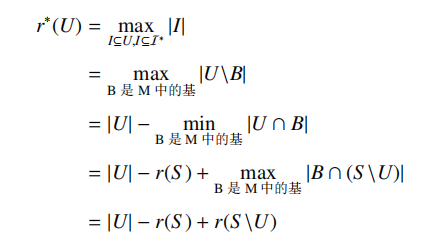
(把 \(S\) 作为全集, \(U\) 作为某个集合的写法,真的让人非常难受)
可以证明新的秩函数满足三个性质,所以这是拟阵。
当然直接证明交换性也是可以的:设 \(A=E+F,B=E+G,F\cap G=\varnothing,|G|>|F|,H=S-E-F-G\) 。如果 \(A\) 加上 \(B\) 任何一个元素都不合法,说明所有与 \(A\) 无交的基都完全包含 \(G\) ,随便拎一个出来,设为 \(I\) 。但是 \(B\) 是合法的,所以至少有一个基 \(J\) 与 \(G\) 无交。容易发现 \(|J\cap H|>|I\cap H|\) 。设 \(K=I\cap H\) ,那么 \(K\) 还可以再多在 \(H\) 里面挑一个元素(交换性)得到 \(K'\) ,然后再用 \(I\) 扩展 \(K'\) ,一定可以得到一个不完全包含 \(G\) 的基。
(麻烦的很)
对偶拟阵的基就是原拟阵的基取补集得到的,所以可以注意到一个拟阵对偶两次之后会回到自己。
4.2 删除和收缩

删除很容易理解,就是把 \(Z\) 删掉了,并且秩函数也不变。
考虑如何理解收缩操作。
先考虑 \(M^*\backslash Z\) 中的独立集是什么:一个不包含 \(Z\) 的集合,使得取补集之后还存在一个基。
那么 \(M^*\backslash Z\) 里的基,就是极大的一个集合,使得取补集之后能和 \(Z\) 里面的某一个极大独立集拼在一起。
那么 \((M^*\backslash Z)^*\) 的独立集,就是需要能和 \(Z\) 中的一个极大独立集拼在一起得到一个 \(M\) 中的独立集。
交换性还是很显然的。
(好扯)
这时候秩函数的强大就又一次体现出来了。我们可以什么都不管,直接推新的秩函数:
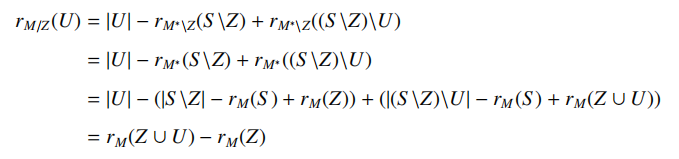
顿时就看出什么意思了。
事实上收缩这个名称可以对应到图拟阵中的缩边操作。
对一个拟阵进行删除或收缩操作之后还是一个拟阵。
4.3 极小元
对一个拟阵 \(M\) 删除和收缩若干次之后得到的任意拟阵 \(M'\) ,称为 \(M\) 的极小元。
5 拟阵的交
正 片 开 始

拟阵交问题就是要找到最大的 \(|I|\) 。
定理 5.1 (最小最大定理):
先证明 \(\max \le \min\) ,即 \(|I|\le r_1(U)+r_2(S\backslash U)\) 。这直接把 \(I\) 拆开即可。
所以现在需要求出一组 \(I\) 和 \(U\) 满足这个等式,就证明了该定理且解决了拟阵交。下面会给出一个算法,但还要一些铺垫工作。
5.1 强基交换定理
正 片 结 束

也就是加上哪些元素没有作用。
引理 5.2 :如果 \(A\subseteq B\) ,那么 \(cl(A)\subseteq cl(B)\) 。
显然 \(e\in A\) 时一定正确,否则直接用次模性 \(r(A \cup\{e\})+r(B) \geq r((A \cup\{e\}) \cap B)+r(B \cup\{e\}) = r(A)+r(B \cup\{e\})\) ,然后两边消去 \(r(A)\) 即可证明。
引理 5.3 :如果 \(e\in cl(A)\) ,那么 \(cl(A)=cl(A\cup \{e\})\) 。
已经证明了 \(cl(A)\subseteq cl(A\cup \{e\})\) ,所以对于 \(f\in cl(A\cup \{e\})\) ,只需要证明 \(f\in cl(A)\) 即可。由于 \(r(A\cup \{e\})=r(A)\) ,所以这其实是废话。
引理 5.4 : \(cl(A)=cl(cl(A))\) 。
用引理 5.3 逐步加入元素即可。

由于 \(B\) 是基,所以 \(B+\{x\}\) 包含唯一的环 \(C\) ,且 \(x\in C\) 。于是 \(x\in cl(C-\{x\})\) 。运用引理 5.2 得 \(cl(C-\{x\})\subseteq cl((A\cup C)-\{x\})\) 。运用引理 5.3 得 \(cl((A\cup C)-\{x\})=cl(A\cup C)\) 。由于 \(A\) 是基,有 \(S=cl(A)\subseteq cl(A\cup C)=cl((A\cup C)-\{x\})\) ,所以 \((A\cup C)-\{x\}\) 包含一个基,设为 \(A'\) 。由于 \(|A'|>|A-\{x\}|\) ,所以存在 \(y\in A'\backslash (A-\{x\})\) 使得 \(A-\{x\}+\{y\}\) 是基,并且显然 \(A'\backslash (A-\{x\})\subseteq C-\{x\}\subseteq B\) ,所以 \(y\) 合法。另外由于 \(C\) 是环,所以 \(C-\{y\}\) (注意 \(x\in C-\{y\}\) )是独立集,然后用 \(B\) 把它补成 \(B-\{y\}+\{x\}\) 即可。
(非常诡异的证明过程)
5.2 算法
正 片 开 始

引理 5.6 :令 \(I,J\) 为两个独立集,且 \(|I|=|J|\) 。那么 \(D_M(I)\) 中存在一个关于 \(I\backslash J\) 和 \(J\backslash I\) 的完美匹配。
为了能使用强基交换定理,强行定义一个新拟阵 \(M'\) ,独立集为 \(\{I':I'\in \mathcal{I},|I'|\le |I|\}\) ,那么 \(I,J\) 就都变成基了。现在任取 \(J\backslash I\) 的一个元素 \(x\) ,可以找到 \(I\backslash J\) 的一个元素 \(y\) ,使得可以交换。那么一定存在边 \((y, x)\) ,并且可以把 \(J\) 变成 \(J-\{x\}+\{y\}\) 并递归。
定理 5.7 :令 \(I\) 是拟阵 \(M\) 的独立集, \(J\) 是一个大小与 \(I\) 相同的集合。如果二分图 \(D_M(I)\) 中存在一个唯一的关于 \(I\backslash J\) 和 \(J\backslash I\) 的完美匹配,那么 \(J\) 也是独立集。
显然可以先把不属于 \(I\backslash J\) 和 \(J\backslash I\) 的点删掉。设前者为左部点,有 \(y_1\cdots y_t\),后者为右部点,有 \(x_1\cdots x_t\) 。
令 \(N\) 是唯一的匹配,不妨设为 \(\{(y_1,x_1),(y_2,x_2),\cdots ,(y_t,x_t)\}\) 。令 \(N\) 中的边从右到左,其它边从左到右。
由于匹配唯一,所以现在图中一定无环。给 \((y_i,x_i)\) 重新分配下标,使得 \(x_1\cdots x_t\) 的拓扑序单调上升。现在可以看出 \(i<j\) 时不存在 \(y_i\to x_j\) 的边。
然后开始使用反证法,设 \(J\) 中含有环 \(C\) ,取最小的 \(i\) 满足 \(x_i\in C\) 。那么对于所有 \(x\in C-\{x_i\}\) ,都不存在 \(y_i\to x\) 的边,即 \(C-\{x_i\}\subseteq cl(I-y_i)\) 。所以 \(cl(C-\{x_i\})\subseteq cl(cl(I-y_i))=cl(I-y_i)\) 。因为 \(C\) 是环,所以 \(x_i\in cl(C-\{x_i\})\) ,所以 \(x_i\in cl(I-y_i)\) ,但这与边 \((y_i,x_i)\) 矛盾,所以 \(J\) 必定是独立集。
(这又是什么神仙证明思路啊?)

然后终于可以开始叙述算法过程了。
令初始的 \(I\) 为 \(\varnothing\) 。定义集合 \(X_1=\{x\notin I:I+\{x\}\in \mathcal{I_1}\},X_2=\{x\notin I:I+\{x\}\in \mathcal{I_2}\}\) 。每次在当前的交换图中找到一条 \(X_1\) 到 \(X_2\) 的最短路径,令其为 \(P\) ,然后令 \(I\gets I\Delta P\) 。称这样一次过程为一次增广过程。重复增广过程,知道找不到路径。此时的 \(I\) 就是最大的,且找到了 \(U=\{z\in S:z \text{ 可以到达 }X_2\}\) 。
注意如果 \(X_1\cap X_2\ne \varnothing\) 那么会直接拓展一个属于交集的元素。
然后为了证明正确性,需要 1. \(|I|\ge r_1(U)+r_2(S\backslash U)\) 2. 算法运行中的任意一个时刻 \(I\Delta P\) 都是公共独立集。
先证明 \(r_1(U)\le |I\cap U|\) 。反证法,如果 \(r_1(U)>|I\cap U|\) ,那么存在 \(x\in U\backslash I\) ,使得 \((I\cap U)+\{x\}\in \mathcal{I}_1\) 。如果 \(I+\{x\}\in \mathcal I_1\) ,那么又有 \(x\in X_1\) ,所以存在一条路径,矛盾;否则 \(I\) 要先删掉若干个元素之后才能加 \(x\) ,由交换性可知只需要删一个,所以存在 \(y\in I\backslash U\) ,使得 \(I-\{y\}+\{x\}\in \mathcal I_1\) ,但这又说明存在 \(y\to x\) 的边,即 \(y\) 能到达 \(X_2\) ,所以 \(y\) 也应该在 \(U\) 中,矛盾。
然后设 \(V=S\backslash U\) ,证明 \(r_2(V)\le |I\cap V|\) 。同样反证法,如果 \(r_2(V)>|I\cap V|\) ,那么存在 \(x\in V\backslash I\) ,使得 \((I\cap V)+\{x\}\in \mathcal I_2\) 。如果 \(I+\{x\}\in \mathcal I_2\) 那么 \(x\in X_2\) ,所以 \(x\in U\) ,矛盾;否则存在 \(y\in I\backslash V\) 使得 \(I-\{y\}+\{x\}\in \mathcal{I}_2\) ,那么有边 \(x\to y\) ,但 \(y\in U\) ,所以 \(x\) 可以到达 \(X_2\) ,矛盾。(这一段自己补的,可能有锅)
最后证明每一步的 \(I\Delta P\) 都是独立集。
令最短路 \(P=(x_0,y_1,x_1,\cdots,y_t,x_t)\) ,令 \(J=\{x_1,\cdots,x_t\}\cup (I\backslash \{y_1,\cdots,y_t\})\) ,那么 \(J=I\) ,且在 \(D_{M_1}(I)\) 中 \(I\backslash J\) 和 \(J\backslash I\) 存在唯一的完美匹配(不然就不是最短路了),所以 \(J\) 是 \(M_1\) 中的独立集。然后考虑加入 \(x_0\) 。既然 \(P\) 是最短路,有 \(x_1,\cdots,x_t\notin X_1\) ,所以 \(r_1(I\cup J)=r_1(I)=r_1(J)\) 。由于 \(I+\{x_0\}\) 是独立集, \(|I+\{x_0\}|>|J|\) ,所以可以给 \(J\) 补一个元素。如果这个元素不是 \(x_0\) 就得到 \(r_1(I\cup J)>r_1(I)\) ,矛盾,所以只能是 \(x_0\) 。
5.3 复杂度
令 \(r=\max(r_1(S),r_2(S))\) ,每次构建出来的图是 \(n\) 个点, \(rn\) 条边(???),要跑 \(r\) 次增广,所以复杂度 \(O(r^2n)\) 。
5.4 带权拟阵的交

(你说是那就是吧)
5.5 多个拟阵的交
NP-Hard
5.6 应用
二分图匹配
匹配本身就是一个拟阵,但判断一个点集是否是独立集也不好直接判断。
考虑直接定义以边为元素的两个拟阵,分别要求左边度数 \(\le 1\) 和右边度数 \(\le 1\) ,那么二分图匹配就可以看做拟阵交。
仔细分析一下发现匈牙利算法找到的增广路和拟阵交中的增广路一样。
(但是我感觉好像不太一样?匈牙利算法没有保证增广路最短吧)
最小树形图
两个拟阵,一是无环,二是除了 \(x\) 以外每个点入度不超过 1 。然后带权拟阵交。
Colourful tree
带权无向图,每条边有一个 1 到 \(n-1\) 的颜色,求一个权最大的生成树,满足每种颜色只出现一次。
显然可以拟阵交。
Rainbow Graph

选取一些边使得图连通并不是拟阵,但图拟阵的对偶拟阵是删掉一些边使得图连通,所以考虑删边。两个限制就是拟阵交。由于拟阵交算法是从小到大扩展,所以每个 \(k\) 的答案都求出来了。
可以看出在限制条件只有两种时,原先看起来莫名其妙的限制现在可以用拟阵交无脑解决。
6 拟阵的并
下面略过了不少证明过程,因为不想看了。
6.1 定义
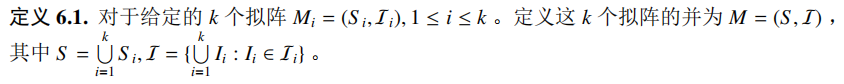
当 \(S_i\) 互不相交时拟阵的并的定义比较显然,即每个部分都要是独立集才能是独立集,并且显然满足拟阵的条件。但是 \(S\) 有交时就比较迷惑。直接解释就是,一个集合是独立集当且仅当存在一个划分成 \(k\) 个子集的方法,使得它们在各自的拟阵中都有定义且是独立集。为什么这是拟阵呢?
先不加证明地给出秩函数的定义。对于给定的 \(k\) 个拟阵 \(M_i\) 的并的拟阵 \(M\) 的秩函数如下:
为了证明这个秩函数的正确性,还要先证明一个引理。
引理 6.2 :令 \(\hat M=(\hat S,\hat {\mathcal I})\) 为任意一个拟阵,且是 \(k\) 个基础集互不相交的拟阵 \(\hat M_i=(\hat S_i,\hat {\mathcal I}_i)\) 的并。对于任意一个函数 \(f:\hat S\to S\) ,定义拟阵 \(M=(S, I)\) ,其中 \(\mathcal{I}=\{f(\hat{I}): \hat{I} \in \hat{\mathcal{I}}\}\) , \(f(\hat I)=\large{\cup}_{x\in \hat I} f(\hat x)\) 。那么 \(M\)的秩函数如下:
其中 \(f^{-1}(e)=\{x:f(x)=e\}\) 。
跳了跳了,看不懂了,不想看了……
6.2 独立集判定问题
虽然证明了拟阵交还是拟阵然而并没有,但判定一个子集是否是独立集也不是很好做。
6.2.1 拟阵交
可以利用拟阵交算法。考虑构造两个拟阵,集合是 \(\{(e,i):e\in U\}\) ,表示把 \(e\) 分到 \(i\) 里面。第一个拟阵限制对于每一个 \(i\) ,选取的 \(e\) 都是独立集;第二个拟阵限制对于每一个 \(e\) 最多只选取了一个 \(i\) 。然后跑拟阵交,看跑出来的最大大小是否等于 \(|U|\) 。
6.2.2 拟阵划分
用玄妙方法直接解决此问题。假设存在一个划分算法,输入 \(M_1\cup \cdots \cup M_k\) 的独立集 \(I\) ,一个关于 \(I\) 的划分 \(I=I_1\cup \cdots \cup I_k,I_i\in \mathcal I_i\) ,和一个不属于 \(I\) 的元素 \(s\) ,判断 \(I+\{s\}\) 是否还是独立集,并给出新的划分,那么就可以支持逐步加元素并判断是否是独立集。
类似定义 5.3 (但边是有向的,从 \(I_i\) 指向 \(S_i\backslash I_i\) ),定义交换图 \(D_{M_i}(I_i)\) ,然后定义当前的交换图 \(D\) 是所有 \(D_{M_i}(I_i)\) 的并,对于每个拟阵定义 \(F_i=\{x\in S_i\backslash I_i:I_i+\{x\}\in \mathcal I_i\}\) ,定义 \(F={\large {\cup}} F_i\) 。
定理 6.3 :对于任一元素 \(s\in S\backslash I\) , \(I+\{s\}\in \mathcal I\) 当且仅当存在一条从 \(F\) 到 \(s\) 的有向路径。
仍然找到最短路径,设为 \(P=\{s_0,s_1,\cdots,s_p\}\) 。不妨设 \(s_0\in F_1\) 。对于 \(1\le j\le k\) 设 \(S_j=\{s_i,s_{j+1}:(s_i,s_{i+1})\in D_{M_j}(I_j)\}\) 。那么令 \(I'_1=(I_1\Delta S_1)\cup s_0\) ,而对于其他的 \(j\) ,令 \(I'_j=I_j\Delta S_j\) (也就是路径上的点除了 \(s_0\) 以外全部往前移了一格,换到另一个拟阵中)。
类似拟阵交中的证明,可以得到现在也是一个合法的划分。
必要性不想看了。
6.3 应用
比如可以特殊化拟阵的并,令 \(M^{k}=M \cup M \cup \cdots \cup M\) ,那么可以判断一个子集是否能划分为不超过 \(k\) 个独立集。
考虑 \(M^k\)的秩函数 \(r_{M^{k}}(U)=\min _{T \subseteq U}\left(|U \backslash T|+k r_{M}(T)\right)\) ,显然最小值会在 \(cl(T)=T\) ,即加任何一个元素都会增大 \(r_M(T)\) 时取到。
定理 6.4 (拟阵基覆盖定理) :一个拟阵 \(M\) 可以被不超过 \(k\) 个基(或是独立集,无所谓)覆盖,当且仅当 \(\forall T\subseteq S,|T|\le kr_M(T)\) 。
可以理解为整个可以被覆盖,当且仅当每个子集都有可能可以被覆盖。
定理 6.5 (拟阵基包含定理) :一个拟阵 \(M\) 可以包含至少 \(k\) 个互不相交的基,当且仅当 \(\forall T\subseteq S,|S \backslash T| \geq k\left(r_{M}(S)-r_{M}(T)\right)\) 。
至少包含 \(k\) 个互不相交的基等价于 \(M^k\) 的秩至少是 \(k\) 倍 \(M\) 的秩。

二分图匹配:设左边有 \(n\) 个点,右边有 \(m\) 个点,那么可以写成 \(m\) 个拟阵的并,每个拟阵的元素集合都是 \(\{x_1,x_2,\cdots,x_n\}\) ,独立集是只有一个点且与 \(y_i\) 有边,那么二分图匹配的答案就是拟阵并的秩。可以发现匈牙利算法和拟阵并算法也是类似的。
元旦老人与丛林

(uoj168)
也就是问能否用两棵生成树覆盖边集。用上面定理 6.6 转化一下,变成最大权闭合子图。
但是 6.6 要求不能选择 \(U=\varnothing\) ,否则 \(|U|-1\) 就不是树边个数了。所以还要枚举强制选一个点,再搞一些操作。
7 拟阵的可表示性
咕了。

