《<最小方差生成树>命题报告》 - 学习笔记

关键是注意到可以枚举平均数。

5 \(T=1\) 的标准解法

可以发现一条边存在的时间一定是一个区间，考虑求出这个区间的左右端点。

可以二分左端点 \(l_i\) ，设自己的权值是 \(w_i\) ，那么合法当且仅当只用 \((2l_i-w_i,w_i)\) 的边无法使得 \(u_i,v_i\) 连通。

发现这东西可以直接转化为二分 \(2l_i-w_i\) ，再发现这东西根本不需要二分，只需要 LCT 动态维护最大生成树即可。

做 \(l_i\) 的时候顺手也可以把 \(r_j\) 求出来。

6 最小乘积生成树

定义一棵生成树的权值为 \(\sum a_i\sum b_j\) ，求最小生成树。

设 \(x=\sum a_i,y=\sum b_i\) ，那么一棵生成树可以对应到二维平面的一个点。容易发现最优的生成树一定处在所有点的下凸壳上。

关于凸壳有一个经典的 wqs 二分算法：任取斜率 \(k\) ，把边的权值看做 \(ka_i+b_i\) 求最小生成树，得到的便是用斜率 \(k\) 的直线切凸壳得到的点。

于是得到一个思路：枚举 \(k\) ，求出所有 \(ka_i+b_i\) 得到的不同最小生成树，在这里面取最小值。

但是 \(m\) 太大了，暴力做会飞。标准解法是找到 \(x\) 和 \(y\) 最小的两个点，然后找离这两个点的直线距离最远的点，可以用上面的方法求出来。然后分治两边。把点视为随机的话不知道怎么凸包上的点数就 \(O(n\log m)\) 了，于是复杂度 \(O(n^3\log n)\) 。

如果直接枚举 \(k\) 那就可以获得 \(O(m^2\log m)\) 做法。

能否证明一条边存在的时间是一个区间呢？答案是不行（

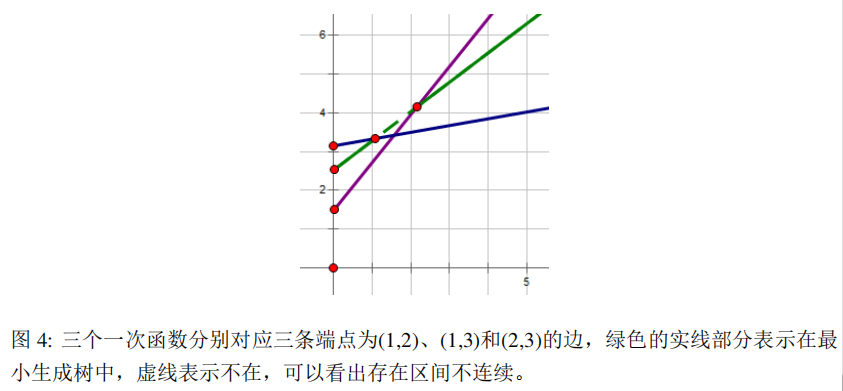
7 \(T=2\) 的算法

此时要求出删掉每条边之后的最小方差生成树的大小。显然只需要对 \(O(n)\) 条树边求答案。

考虑删掉 \(k\) 之后其它边的 \(l,r\) 会怎么变化。显然只有 \(l_i,i>k\) 和 \(r_i,i<k\) 会变化，但还可以更进一步，证明只有 \(G(V,E_{e<k})\) 的最大生成树 \(T_l\) 的 \(r\) 会变化， \(G(V,E_{e>k})\) 的最小生成树 \(T_r\) 的 \(l\) 会变化。

由于对称性，只需要证明不在 \(T_r\) 里的边的 \(l\) 不会变化。这其实很好证明，因为走到 \(i\) 时，它在当前最大生成树上对应的链上的边的编号一定都大于 \(k\) 了，所以换掉的边也会和以前一样。

那么就自然引出了这样的做法：初始令生成树为 \(T_l\) ，然后把 \(T_r\) 里的边从小到大加入，得到新的 \(l\) 和 \(r\) 。

一共要做 \(n\) 次，于是复杂度 \(O(n^2\log n+nm)\) 。然而子任务 8 需要高精度，较大的常数强行把这个做法卡掉了。

注意到现在的复杂度瓶颈是每一次算答案的 \(O(nm)\) ，所以要在修改 \(O(n)\) 个 \(l,r\) 之后快速维护出答案。

然后就是瞎 jb 线段树维护凸包，不想看了。