《浅谈信息学竞赛中的独立集问题》 - 学习笔记
看起来很有趣。来提升一下乱搞技巧。


3 一般图的独立集问题
3.1 基于极大独立集搜索的独立集算法
显然最大独立集一定是极大独立集,所以考虑把极大独立集搜出来,也许能带来优化。
3.1.2 极大独立集与 Bron-Kerbosch 算法
其实是一个很简单的算法。考虑任意一个点 \(u\) ,那么 \(u\cup N(u)\) 里面显然至少会有一个点在极大独立集内。
现在维护集合 \(R,P,X\) ,分别表示已经确定的当前集合、还可以加入的点的集合、钦定不能加入的点的集合。找到 \(u\in P\cup X\) 。使得 \(|u\cup N(u)|\) 最小,然后枚举 \(v\in P\cap (u\cup N(u))\) :
- 递归搜索 \(R\cup v,P-(v\cup N(v)),X-(v\cup N(v))\) 。
- 把 \(v\) 从 \(P\) 中删去,加入 \(X\) 。
显然所有极大独立集都会被搜到。
3.1.3 极大独立集的个数
上面这个算法可以被证明递归调用次数是 \(O(3^{n/3})\) 的。
然后可以算算随机图的期望极大独立集个数,有
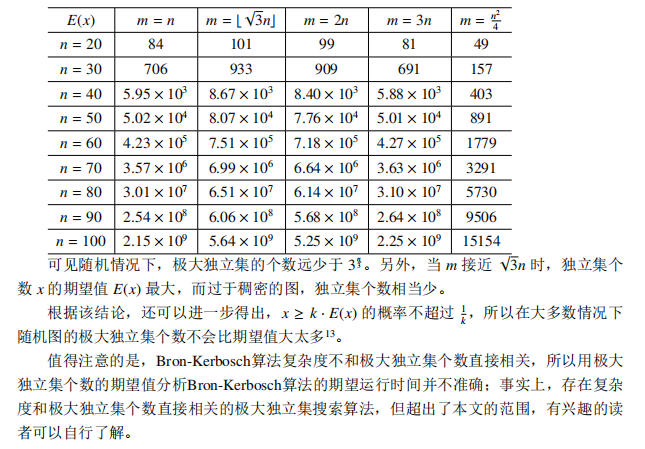
3.2 基于动态规划的独立集算法
DP 当然更高级一点,还可以求解独立集计数等问题。
但这个 DP 其实近于爆搜:直接设 \(dp_S\) 表示 \(G[S]\) 上的最大独立集,然后随便拿出一个点 \(v\) ,就有
如果每次拿出编号最大的点,那么可以做到不重不漏,并且复杂度 \(O(2^{n/2})\) ,因为前 \(n/2\) 层每层只有 2 种递归的可能,后 \(2^{n/2}\) 层 \(S\) 只包含后面 \(n/2\) 个点。卡满也非常简单,放 \(n/2\) 个独立的两个点的连通块即可。或者如果没加剪枝的话 \(m=0\) 的图就可以卡满了。
然后是两个简单的剪枝:
- \(v\) 取 \(G[S]\) 中度数最大的点。显然这样还是不重不漏。
- \(S\) 不连通时拆开分别计数。
这样就跑得飞快。
还有一个优化是在 \(G[S]\) 是一棵树时改成树形 DP ,但好像没啥用。
一个小问题是这个算法的空间复杂度比较爆炸,可以只记忆化 \(S\) 较小的 \(dp\) 值。
求所有大小为 \(k\) 的独立集的权值(所有点权值之积)之和的简单代码:
ll W[sz],out[sz];
map<ll,vector<ll>>dp;
vector<ll> work(ll S)
{
vector<ll>res; int c=__builtin_popcountll(S); res.resize(c+1);
if (!S) return res[0]=1,res;
if (dp.count(S)) return dp[S];
if (c>10)
{
ll cur=S&-S;
rep(i,1,c) rep(k,0,n-1) if (cur>>k&1) cur|=out[k],cur&=S;
if (cur!=S)
{
auto r1=work(cur),r2=work(S^cur);
rep(i,0,(int)r1.size()-1) rep(j,0,(int)r2.size()-1) (res[i+j]+=r1[i]*r2[j]%mod)%=mod;
return res;
}
}
int mx=-1,p=-1; rep(i,0,n-1) if ((S>>i&1)&&chkmax(mx,__builtin_popcountll(S&out[i]))) p=i;
auto r1=work(1ll<<p^S); rep(i,0,c-1) res[i]=r1[i];
auto r2=work(S&(~out[p])); rep(i,0,(int)r2.size()-1) (res[i+1]+=r2[i]*W[p])%=mod;
if (c<=n/2) dp[S]=res; return res;
}
3.2.4 测试与对比
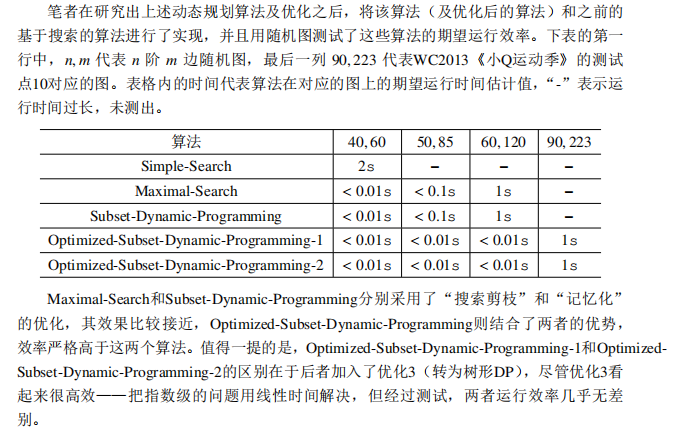
4 特殊图的独立集问题
二分图大家都会,分层图也没什么好说的。
4.4 "\(k\)-仙人图" 上的动态规划
仙人掌的 dfs 树满足每条树边最多被非树边覆盖一次,所以也可以随便 DP 。更进一步,如果满足每条边最多属于 \(k\) 个简单环,其中 \(k\) 为常数,那么都可以在树上状压 DP 解决。
4.1.2 无爪图的最大独立集
在无爪图 (claw-free graph) 上也有多项式做法。无爪图就是不存在 \(K_{1,3}\) 导出子图的图。
集训队论文把这一段写得很简略,于是我跑去看了参考资料。
我就是论文翻译机
有一个类比:考虑一个任意图的线图,它都一定是一个无爪图。线图上的独立集就会对应回原图的一个匹配,而一般图匹配算法是有多项式做法的。
然而并不是任意一个无爪图都能对应回一个原图,所以还要操作。
无爪图有一个重要性质:两个独立集的对称差的导出子图满足每个点的度数都小于等于 2 ,不难证明。也就是说对称差的导出子图的每个连通块要么是环,要么是链。
设 \(I_1,I_2\) 为两个独立集,且 \(|I_1|<|I_2|\) ,那么 \(I_1\Delta I_2\) 一定有一条链,满足首尾都不属于 \(I_1\) 。翻转这条链的状态即可使得 \(|I_1|\) 增大。
所以从 \(I=\varnothing\) 开始,设黑点为在 \(I\) 中的点,白点为不在 \(I\) 中的点。每次的目标就是找到一条黑白交错的链,满足链上的点两两不同,任意两个白点不相邻,首尾都为白色,且首尾都只和一个黑点相邻。链长度 \(\le 3\) 可以先特判掉。
无爪图的一个性质:以下两个图不可能作为子图(不一定是导出子图)存在。
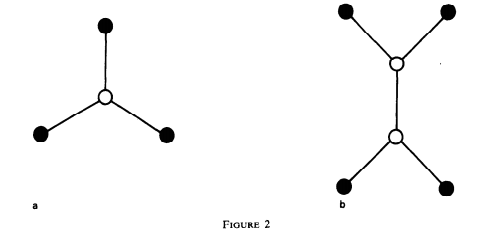
于是“任意两个白点不相邻”可以写得更简洁一点,只需要满足首尾不相邻且隔着一个黑点的白点不相邻即可。画画图即可证明。
现在可以枚举起终点,删除所有和它们相邻的白点,删除所有只和一个黑点相邻的白点,然后尝试找一条增广路。现在的图还满足性质:两个白点之间有边,仅当它们与一个公共黑点相邻(证明见上图右边)。把现在这个图叫做一个 Reduced Basic Structure (RBS) 。
4. A Useful Theorem
然后证明一个(暂时看不懂有什么用的)定理。设 \(S\) 是一个非空集合, \(R\) 是一个 symmetric relation on S 。记 \(xRy\) 表示 x is related to y ,否则 \(xR'y\) 。设 T-property 对于三元组 \((x,y,z)\) 满足,当且仅当 \(xRy,yRz,zRx\) 恰好有奇数个成立。可以发现如果 T-property 对于所有三元组成立,那么 \(R\) 是在 \(S\) 上的一个等价关系,并且把 \(S\) 划分为至多两个等价类。
现在设 \(\{S_\alpha:\alpha\in A,\text {an index-set}\}\) 为一个对 \(S\) 的固定的划分,且划分出来至少三个非空子集。把划分出来的子集叫做 wings 。对于一个 symmetric relation \(R\) ,定义 \(x\bar{R}y\) 当且仅当 \(xRy\) 且 \(x,y\) 属于不同的 wing 。也就是说 \(\bar R\) 只保留 \(R\) 关于不同 wing 的元素的信息。如果 \(R\) 对于两两不在同一个 wing 的三元组 \((x,y,z)\) 满足 T-property ,那么就称 \(R\) 满足 PT-property ,且显然 \(\bar R\) 也满足。
可以证明,如果 \(L\) 满足 PT-property ,那么存在唯一的一个 \(R\) ,使得 \(\bar R=\bar L\) ,且 \(R\) 对于所有 \((x,y,z)\) 都满足 T-property 。
上面有点不说人话。就是对于一个完全 \(k\)-分图 (\(k\ge 3\)) ,任取一种给边红绿染色的方案,使得任意一个三角形都有奇数个红边,那么就有唯一一种给点黑白染色(不考虑 swap(black,white) )的方案,使得红边连接同色点,绿边连接不同色点。
证明这个东西有什么用呢?注意到图中
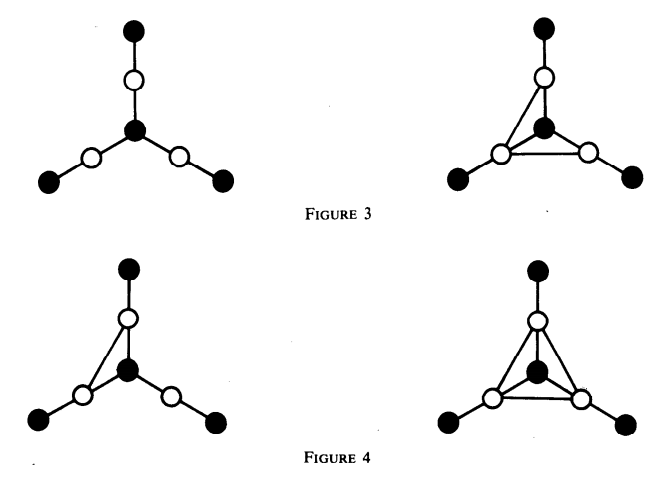
上面两个不可能作为导出子图出现,而下面两个可能出现。
5. Classification Of Black Vertices
现在考虑一个 RBS ,我们来把黑点分类。
任取一个黑点,考虑和它相邻的白点,把这些白点按照相邻的另一个黑点分成几个 wings ,每个 wing 中的另一个黑点叫做 the tip of the wing 。如果这些白点中有一个是只和它相邻的(即增广路的起点或终点),那么把这个黑点叫做“一类规则点”;否则如果它有至少 3 个 wings ,那么叫做“二类规则点”;否则如果有恰好两个 wings ,那么叫做“不规则点”;否则叫做垃圾“无用点“。
显然无用点和与它相邻的白点可以全部删掉。
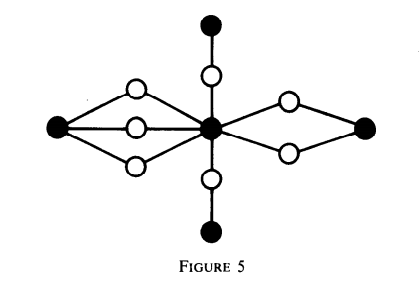
(省略了白点之间的连边)
(注意这个结构与 Figure 3,4 之间的关系)
(整个图就是由若干个这样的结构拼成的,已经看到解题的希望了)
注意到一个增广路就是经过了若干个 wings ,每个 wing 踩一个白点,所以同一个 wing 的白点之间的边已经不重要了。
现在对于每个“规则点”,用如下方法把相邻的白点分成两个子集。
对于一类规则点,把起点/终点单独放一个类型,其他点全部放到另一个类型;对于二类规则点,按照 wing 把点集拆开,然后设 \(\bar L\) 表示两个不同 wing 的点之间是否有边,然后就可以用上面那个定理唯一地把点集拆成两个等价类。
这个定理的作用已经浮现出来了:同一个 wing 内部的边对最终结果没有影响,所以不需要考虑,任意分配。分成两个等价类之后,就只能从一边走到另一边了。
7. Construction Of The Edmonds'-Graph
已经不是很想继续看了。
大概是把黑点换回黑边,分成的两个白点等价类分别变成连向黑边的两个端点的一堆白边,然后就得到原图了。这个原图的线图虽然不是当前的图,但应该性质是类似的。
(显然这句话很不严谨)
所以就可以用类似带花树的算法求出增广路。
(学完之后感觉没什么用啊,我又写不出来 /kk )


