Atcoder刷题记录

诈尸。

ARC066C Addition and Subtraction Hard

首先要发现两个性质：

加号右边不会有括号：显然，有括号也可以被删去，答案不变。
$op_i$和$A_{i+1}$之间只会有一个括号：有多个括号的话只保留最外边那个，答案不变。

然后就可以定义状态：$dp_{i,j}$表示前$i$个数，还有$j$个未闭合的左括号，得到的最大答案。

由于只有减号右边有括号，所以只要知道左边有几个未闭合的左括号，就可以知道自己的贡献是$1$还是$-1$，所以转移也很容易了。

然而状态是$O(n^2)$的，不怎么行。

然而还可以发现一个性质：嵌套的括号不超过两层。超过两层的可以通过调整顺序消去一多余的。

那么就做完了。

AGC033C Removing Coins

首先可以发现，每次操作就相当于两种选择：要么删掉所有叶子，要么留下一个叶子删掉剩下的。

然后再可以发现：每次操作可以选择把树的直径减少$1$或$2$。

那么求出树的直径之后就变成了一个简单的取石子游戏了。

AGC014D Black and White Tree

从叶子开始考虑。如果白点点了叶子的父亲，那么黑点就必须点掉这个叶子，然后这两个点就对后面没有影响了，可以删掉。

冷静思考一番，发现只要一直这样删删删，看最后有没有点剩下来就好了。

ARC063F Snuke's Coloring 2

为了方便，假设四周都有一些点。

问题显然可以转化为：求周长最大且内部没有点的矩形。

首先注意到一点：答案至少为$2(\max(W,H)+1)$。

根据这一点，可以得到一个性质：矩形至少过$x=\lfloor W/2\rfloor$和$y=\lfloor H/2\rfloor$ 中的一条直线。

如果两条直线都不经过，那么就算一个点都没有，也不会达到下界。

既然两种情况那么像，接下来只考虑过$x=\lfloor W/2\rfloor$的情况。

考虑枚举上边界$y_r$、下边界$y_l$，设$x_l=\max\{x_i|y_i\in[y_l,y_r],x_i\le \lfloor W/2\rfloor\}$，$x_r=\min\{x_i|y_i\in[y_l,y_r],x_i\ge \lfloor W/2\rfloor\}$。

那么答案就是$2(y_r-y_l+x_r-x_l)$。

考虑优化，只从下往上枚举$y_r$，用单调栈+线段树动态维护每个$y_l$的答案，复杂度$O(n\log n)$。

ARC068F Solitaire

考虑一个合法的双端队列是什么样子——肯定是形如$P_11P_2$，其中$P_1$为单调下降序列，$P_2$为单调上升序列。（形象一点就是一个V）

既然第$K$个必须是1，那么前$K-1$个数必须能拆成两个可以为空的单调下降序列，而且后面$n-K$个数小于两个序列的结尾的最大值。

于是可以开始DP：设$dp_{i,j}$表示前$i$个数，较小的结尾的数是$j$，的方案数。

考虑下一个接的数$k$与$j$的大小关系：

$j>k,dp_{i,j}\rightarrow dp_{i+1,k}$。
$k>j$，注意此时$k$只能放没有出现过的数的最大值，其它都是不合法的，所以有$dp_{i,j}\rightarrow dp_{i,j+1}$。

第一个转移用前缀和优化一下。

统计答案时考虑没有出现过的$n-K$个数有$2^{\max(0,n-K-1)}$种放法，乘上去即可。

ARC078F Mole and Abandoned Mine

删掉的边权值最小转化为保留的最多。显然，最后剩下的图一定时连通的。

那么可以得到一个性质：从$1$到$n$上的路径的每一条边都是桥，连接两个连通块。如果把路径上的边删掉，那么这些连通块之间没有边，每一个连通块也只和路径上一个点连通。

于是可以开始DP：设$dp_{S,x}$表示当前与$1$连通的点集是$S$，路径末端的点是$x$，的方案数。

转移有两种：往$x$点连上一个连通块$T$并把$T$中的边都连上，或是从$x$往$y$连一条边并把终点置为$y$。

AGC001F Wide Swap

首先转化一下：设$q_{p_i}=i$，那么变为每次在$|q_i-q_{i+1}|\ge K$时可以交换$q_i,q_{i+1}$，最后要使得$1,2,\cdots$在$q$中出现的位置尽量靠左。

那么可以发现，若$|q_i-q_j|<K$，那么$q_i$与$q_j$的位置关系永远不变。

放回到$p$中，就是如果$|i-j|<K$，那么$p_i$和$p_j$的大小关系永远不变。

也就是说，若$p_i<p_j$，那么就一定有$p'_i<p'_j$。

那么可以建出一个图：若$p_i<p_j,|i-j|<K$，那么连一条$i\rightarrow j$的边，表示$p'_i<p'_j$。

然后给每一个点编号，要求字典序最小。

这个问题有一个这样的解法：设当前出度为0且编号最大的点为$x$，那么把$x$标号为$n$，然后删去$x$，--n。

为什么是对的？若$x$标为$w$，那么把$x$变为$n$，把原标号为$[w+1,n]$的点的标号都减一，显然更优。

然后怎么实现它呢？

发现每次需要找最右边的$i$，使得对于$j\in (i-K,i+K)$且$j$没被删，都有$p_j<p_i$。

把原数列每$K$个分一组，那么位置$i$可以被选必须有$p_i$是自己组的最大值。

那么其实每组每次最多只会有一个位置可选，而删掉一个位置之后也只需要更新旁边三组的位置。

线段树随便搞搞就好了。

AGC003D Anticube

考虑相乘起来为$x^3\le 10^{20}$，那么$x\le 10^{10/3}$，$x$中最多只有一个$\ge10^{5/3}$的质因数，$x^3$中最多有三个。

所以$s$中不会有$\ge 10^5$的质因数，否则可以直接被加入答案。

把$[1,10^{10/3}]$的质数筛出来，设$s=\prod p_i^{w_i},a_i=w_i\%3,s'=\prod p_i^{a_i}$，那么接下来可以只考虑$s'$。

求$s'$的方法：若$s$除掉$[1,10^{10/3}]$的质数之后不为1，那么可以简单判一下是不是$(10^{10/3},10^5]$的质数（或平方）。

把$s'$求出来之后，每个数能与它组成三次方数的数是惟一的，可以简单地选取更大的那个子集。

AGC003E Sequential operations on Sequence

首先，显然可以用一个单调栈把$q$变成单调上升的序列。

然后，注意到每次操作就是把原序列复制几遍，再接上一个前缀。

那么可以dp：记$f_i$表示第$i$次操作之后的序列在最终序列中出现的次数。

每一次可以转移：$f_i=f_{i+1}\times \lfloor q_{i+1}/q_i\rfloor$。

但是那个前缀怎么办？

前缀并不会计入$f_i$，但会被算进$f_j(j<i)$，所以往前面递归，看它们出现了多少次。

注意到每次前缀长度会对$q_j$取模，而$q_j\le len$时$len$至少变小一半，所以只会变化$\log len$次，可以二分出下一次变化的地方。

最后递归到第一次还有剩余时就直接加入答案即可。

AGC004C AND Grid

构造题……

发现周边格子不会有紫色，这很有趣。

于是就有了这样一个构造方法：上面红，下面蓝，奇数列红，偶数列蓝。

显然这是满足条件的，可是又是怎么想出来的呢？？

AGC004E Salvage Robots

注意到机器人动其实等价于出口和边界在动。

注意到出口一旦动，那么它动的整个矩形里还没有自爆的机器人都会被救。

也就是说，若出口向右4格向上2格，那么这个$2\times 4$的矩形里的机器人都会被救。

于是DP：记$f_{l,r,u,d}$表示出口走了$(l,r,u,d)$，最多被救多少个。

注意走了$(l,r,u,d)$时整个大矩形的左边$r$列肯定已经没有机器人了，$l,u,d$同理，转移时要注意。

AGC004F Namori

神仙模型转化……

树

注意到树是一个二分图，那么可以先黑白染色一下。

然后做一个奇特的转化：把奇数层的点的颜色反转一下，那么每次操作就变成了交换相邻颜色不同的点的颜色，目标是反转每个点的颜色。

记黑点权值为$1$，白点权值为$-1$，那么总权值必须为$0$，否则无解。

再神奇地转化一下：黑点上有个球，白点上有个洞，每次可以把一个球滚进去相邻的一个空的洞里，最后每个洞里都要有一个球。

考虑每条边被滚过的次数，就是子树中球和洞的个数差，所以答案就是

\[\sum_x|sum_x| \]

奇环

任意删掉环上一条边，现在相当于这条边的两个端点可以同时出现或消失球。

那么如果$2\nmid sum_1$就无解，否则增加的球数是固定的，直接算即可。

偶环

任意删掉环上一条边，现在相当于这条边的两个端点可以一边出现球，另一边消失等量的球。

那么显然$sum_1\ne 0$时无解，否则设这条边为$(u,v),dep_u<dep_v$，$v$点出现$k$个球（或消失$-k$个球），那么$(u,v)$这条链的贡献就变为了

\[sum_u+\sum_{x\in(u,v),x\ne u} |sum_x+k| \]

这就是个数轴上使总距离最小的题，取中位数即可。

AGC005E Sugigma: The Showdown

如果想到怎么判-1那么就很好做，但谁会直接想什么时候-1呢？

考虑红树上的每一条边$(u,v)$，如果蓝树上$dis(u,v)>2$（$dis(u,v)$指两点之间的边数），而且sigma可以比sugim先到某个端点，那么sigma就可以在这条边上跳来跳去，而sugim永远也抓不到。

如果没有这样的边，在蓝树上以sugim的出发点为根，那么sigma只能往父亲、父亲的父亲、子树内、兄弟这几个地方跳，sugim步步为营，总能抓到的。

那么他到底能存活多久呢？按照贪心的策略，当然是在不被抓到的情况下跑到蓝树上深度最深的点，然后乖乖等死。这个可以一个bfs搞定。

AGC005F Many Easy Problems

这题还真不怎么像AGC的题。

考虑点$x$对$f_k$的贡献：没有贡献时要么是全都在祖先那里，要么是全都在某个儿子的子树里，所以贡献是

\[{n\choose k}-{n-size_x\choose k}-\sum_v {size_v\choose k} \]

把所有贡献加起来，就是

\[n{n\choose k}-\sum_{x=2}^n \left( {size_x\choose k}+{n-size_x\choose k} \right) \]

把$size$和$n-size$放到桶里，那么答案就是

\[n{n\choose k}-\frac 1 {k!} \sum_{i=1}^n cnt_ii!\times \frac 1 {(i-k)!} \]

显然是个卷积，NTT一下即可。

AGC006C Rabbit Exercise

见过的套路题……但还是没做出来……

如果本来是$x_{i-1},x_i,x_{i+1}$，然后搞了$x$，那么$x_i$的期望就会变成$x_{i+1}+x_{i-1}-x_i$。

然后发现似乎可以直接把期望丢回去，就当做$x_i$变成了$x_{i+1}+x_{i-1}-x_i$。

然后……

然后差分一下，发现一次操作就是交换相邻两项，然后记录一组操作之后会发生什么，然后倍增。

AGC006D Median Pyramid Hard

容易想到二分答案，然后底下转化为01串。

手造数据找规律，发现离中心最近的连续两个相同格子的数就是答案。

也有可能没有连续的，特判一下即可。

AGC006E Rotate 3x3

容易发现一列肯定一起动，而且只有递增/递减两种情况。

定义交换表示换位置，翻转表示换状态。

容易发现奇列怎么换都不会换到偶列。

手玩之后发现可以同时翻转相邻的奇列/偶列。

发现一次操作后有一组位移、三个翻转，而三个翻转其实可以变成一个。

更精确地讲，交换相邻奇列的唯一副作用就是翻转中间的偶列。

全都归位之后又可以同时翻转两列。

总的来说，就是奇列的交换次数要与偶列的交换次数同奇偶、偶列的交换次数要与奇列的交换次数同奇偶。

AGC006F Blackout

神仙题……

考虑到棋盘太大，也不好想象，就把它转成图。

现在：如果有边$(x,y),(y,z)$，那么连上$(z,x)$。

脑抽想到三染色：对于每个弱连通分量（有向看作无向），规定如果有边$(x,y)$，那么$col_y=(col_x+1)\text{ mod } 3 $，然后会有三种情况：

第一种：有两种颜色且存在合法方案——容易发现这样一条新边都连不了。

第二种：有三种颜色且存在合法方案——可以发现此时所有$(0,1),(1,2),(2,0)$的边都能连了。

第三种：无合法方案——可以发现此时所有边都能连上，包括自环。

于是dfs一下就做完了。

AGC007C Pushing Balls

又是一道神仙题，做不来qwq

首先把题目抽象成$2n+1$个端点，每次等概率删除两个相邻端点，并加上他们的距离。

发现题目给的等差数列这个条件特别奇怪，于是可以列几个小数据来看做完一次操作后第$i$个区间的期望长度。（这里的第$i$个是重新编号的）

然后发现它竟然还是个等差数列！！

然后就假装每次都还是等差数列，继续做就好了。

AGC007E Shik and Travel

显然进了一棵子树就要把这棵子树的叶子走完再上去。

我们先二分答案，然后状态可以被抽象成二元组$(a,b)$，表示从这里下去还要再走$a$的距离，上来要走$b$的距离。在每个点把可用状态全都存下来，注意如果$a\le a',b\le b'$那么$(a',b')$就废了。

在非叶子节点合并的时候可以发现对于$(a,b)$，要选一个$a'$尽量大的方案与它合并，所以直接二分+启发式合并就好了。

AGC007F Shik and Copying String

首先从右往左贪心的思路非常显然，但这个思路比较模糊，我们需要把它抽象成数学模型。

我们可以把向右覆盖的操作看作向右的水平线段，而继承到下一个版本的操作看作竖直线段，那么每个字母都可以被看作是一段折线，我们就是要在折线互不相交的情况下使时间最少。

画画图可以发现，折线的转折点会贴着上一条折线走，即在上一个转折的基础上向左向下一格。

于是可以维护一个队列来判断当前折线会走到上一条的哪个转折后停下，也就可以算出答案了。

感觉很难讲得明白，贴个代码：

int ans=0,pos=n;
drep(i,n,1)
{
	if (t[i]==t[i-1]) continue;
	chkmin(pos,i);
	int cur=i;while (t[cur+1]==t[i]) ++cur;
	while (l<=r)
	{
		int x=q[l]-(r-l);
		if (cur>=x) break;
		++l;
	} 
	while (pos&&s[pos]!=t[i]) --pos;
	if (!pos) return puts("-1"),0;
	q[++r]=pos;
	chkmax(ans,r-l+1);
}

AGC008C Tetromino Tiling

首先通过手玩，可以发现只有1245可以用，而2可以单独考虑，所以只用管145。

145只有几种玩法：1+4+5，1+1，4+4，5+5。

于是随便判一下即可。

AGC008D K-th K

直接按顺序贪心地放次数还不够的数，没得放了就放已经完成的数。

AGC008E Next or Nextnext

建图，对于某个合法方案$p$，连$i\rightarrow p_i$，那么一定可以组成若干个环。

再连$i\rightarrow a_i$，那么这条边在环上一定只有两种情况：和原来的边一样，或是跳过了一个点，到了下一个点。

如果所有边都一样，那么显然还是原来那个环。

如果所有边都跳了一下，那么如果环是奇环就还是一个环，否则就会分裂成两个环。

如果有些跳有些不跳，那么就变成了一棵特殊的基环树，这里的“树”其实是一条链。

现在我们手上有$i\rightarrow a_i$的图，考虑如何复原出$i\rightarrow p_i$的图。

对于长度相等的简单环可以一起考虑，分自己成一个环和与前面环合并来讨论。

对于基环树，要把那些多出来的链塞回去。由于我懒得画图，所以比较难讲明白，可以去看这里。（Orz litble）

AGC008F Black Radius

这题的难点其实就是枚举的时候要做到不重复，所以我们先把每一个合法连通块与另外一种表示方法唯一对应起来。记这个连通块的直径的中点为$x$（$x$也可以是一条边），半径为$d$，那么二元组$(x,d)$就唯一表示了一个合法连通块。（画画图感受一下可以证，不过感觉这种题都是要先猜结论再慢慢证的）

现在我们的任务：枚举$x$，算出有多少个$d$是合法的。

如果$x$是连接$u,v$的边，且$mxdep_u\le mxdep_v$，那么显然我们要填满子树$u$，然后再延伸到$v$，否则$x$就不会是中心。于是当$u$子树内有好点的时候它对答案有1的贡献。

否则，感性理解一下，合法的$d$一定组成了一个区间。我们分两种情况讨论。

1. $x$是好点。此时显然下界为0。设以$x$为根的时候$x$的儿子分别为$u_1,u_2,\cdots$，那么上界就是$mxdep_u$的次大值。

2.$x$不是好点。此时可以发现上界没有变化，而下界则成为了$\min\{mxdep_u|v\in tree_u,v\ is\ good \}$。

于是$O(n)$的树形DP做一遍即可。

（通过上面的分析其实也证明了$d$组成了一个区间）

AGC009D Uninity

首先要做一个转化：以$v$为中心点合并一些权值为$k$的树的时候，把$v$的权值赋为$k+1$，于是题目就转化为求一种编号方法，使得任意两个权值为$k$的点之间有权值更大的点，最小化最大权值。

（证明：任意一种原方案显然可以转化为一种合法的编号方案，而一种合法的编号方案可以每次提出权值最大的点，转化为合法原方案）

发现可以贪心。对于每棵子树，记录哪些权值到根的路径上没有更大的权值（记为“出现”）。合并子树的时候看一下同时有两个出现的最大权值$k$是多少，然后自己就取$k+1$，把$[0,k]$都记为未出现。（本质就是取能被取的最小权值，因为取更大的权值显然没有益处）

根据点分治的思想，最大权值肯定不会超过$\log n$，所以可以直接开数组。

AGC009E Eternal Average

首先还是要做一个转化：把求平均值的操作看做一棵$k$叉树，0/1都在叶子上，非叶子节点的权值是$k$个儿子的平均数。

考虑每个1对根节点的贡献，其实就是$k^{-dep_x}$。

这个分数如此的不友善，所以我们要把它变得好看一点。把最后的结果写成$k$进制，那么就会变成

\[0.s_1s_2s_3s_4s_5\cdots s_l \]

这个式子必须满足一些条件：

\[\sum s=m\pmod{k-1}\\ 1+l\times (k-1)-\sum s\le n \]

（条件的意思：1. 考虑进位之后，各位数字之和要与$m$同余；2. $n$个0要足够把它补成一棵完全二叉树）

然后就可以DP：设$dp_{i,j}$表示小数点前$i$位，数位和为$j$，的方案数。前缀和优化一下即可。

AGC010C Cleaning

经典题，但就是没做过，所以自闭了。

可以发现点权确定之后就可以确定每条边的边权：对于叶子节点，他的点权等于连向父亲的边权；对于非叶子节点，他的点权等于周围边权之和。容易发现只要这样一路推上去即可得到每条边的边权。

如何凑出方案呢？容易发现，只需要这个点旁边的边权的最大值不超过总和的一半，那么就一定可以相互抵消成0，所以一定有解。

所以dfs一次就完事了。

AGC010D Decrementing

博弈论怎么可能做得出来呢……

首先要发现，当局面有奇有偶的时候，除以$\gcd$操作必然不改变奇偶性。

注意到一个关键性质：结束局面必然全是1，也就是没有偶数。于是可以推出：当当前局面没有偶数的时候，你只能变出一个偶数来，而对手一定又可以变回去，直到你输掉。所以，全奇数的局面是必败的。

有偶数呢？我们对偶数个数的奇偶性分类讨论。

奇数个偶数时，你操作一个偶数变为奇数，对方不管如何处理，偶数个数的奇偶性不变。最后总能到达你操作完之后全是奇数的必败态。所以，偶数个数为奇数的时候必胜。

偶数个偶数时，显然操作偶数之后会到达必胜态，所以要操作奇数。如果不止一个奇数那么肯定也输了，而只有一个奇数的话就会所有数除以2，事情可能会发生转机，所以要递归处理。

显然递归层数不超过$\log a_i$，所以可以直接暴力。

AGC010E Rearranging

我已经摸到AGC的套路了：一旦不会做就乱连个边，乱建个图，然后就对了。

（手动狗头保命）

可以发现，定下初始序列之后，不互质的数的相对顺序不会改变。

我们把不互质的数连起边来，成为若干个连通块，现在单独考虑每个连通块。

如果要最小化每个连通块的顺序的字典序怎么做呢？显然第一个可以放最小的，但这也就限制了第二个必须与第一个有边相连，同时也限制了后面的……但是没有关系，只要每次选与自己有边的、编号最小的往后dfs即可。

假设我们固定了每个连通块的顺序呢？可以发现后手一定会贪心地每次取最大的往前填，所以只要最小化每个连通块字典序即可。

AGC010F Tree Game

怎么这题反而比前面的题更简单……怎么我还是做不出来……

首先为了方便，每次判断一个点是否合法的时候就直接把他提到根，然后来判断每个点是否为必胜态。

对于$u$，如果有一个儿子$v$满足$a_u>a_v$，那么显然在$u,v$之间反复横跳是先手赢的，所以后手只能往$v$的儿子走，所以可以只考虑$v$的子树，递归处理。如果先手往$u$的父亲走呢？那么这一定说明先手已经不能往儿子走了，而原来的后手又为什么从$u$的父亲走到了$u$呢？这一定说明$a_{fa_u}>a_u$，所以后手只需要逼得先手在$fa_u,u$左右横跳就可以稳操胜券，所以先手必然不会往上走。

所以枚举答案，$O(n)$判断，就做完了。

ARC070E NarrowRectangles

一开始想了个假贪心，把自己叉掉之后就可以开始想DP了。

容易想到，设$dp_{i,j}$表示前$i$段已经联通，最后那个的左端点的坐标是$j$，的最小代价。随手画画图，可以发现他一定关于$j$是一个分段函数，而且是一个凸包，而且斜率在$[-i,i]$里，而且是连续的整数。于是只需维护每个分段点在哪里就可以知道凸包的形式。

转移的时候，发现一定是把中间一段推平，而两边由平移而来，最后加上一个绝对值函数。我们只需要每次转移的时候把最低点的纵坐标加进答案里，然后假装最低点在$x$轴上。

分类讨论：如果加上的函数的0点在被推平的区间里，那么新顶点显然。否则，如果在左边，那么新的最小值就在原来斜率$-2,-1,0$的分界点中间。如果在右边则同理。

所以直接搞两个优先队列维护左右分界点即可。

ARC070F HonestOrUnkind

首先想一下如何判无解。

可以发现，当假人数量大于等于真人的时候，可以有一部分假人伪装成真人，所以肯定无法知道谁是真人，此时无解。

然后就是各种脑洞做法，这里只讲其中一种好懂的。

发现一个性质：如果$x$说$y$假假，那么$x,y$必然不会全是真人。

于是可以发现：如果删掉$x,y$，那么真人数量一定还是大于假人。

所以可以维护一个栈，栈里面$a_i$说$a_{i+1}$是真人。

当加入当前这个人的时候，如果栈顶说他是真人，就把他加进去，否则就直接把这个人和栈顶都删掉。

最后考虑栈内的情况。由于有真人比假人多的限制，不可能全是假人。而显然又不可能出现某个真人前面是假人的情况，否则栈顶必然是真人。

AGC036F Square Constraints

我们以$i$为横坐标，$p_i$为纵坐标，发现满足条件的点在四分之一个圆环内。记$[l_i,r_i]$表示$p_i$所在的区间。

观察这个圆环，发现如果没有$x\in [0,n]$的点的$y$的限制，那么就是一个这样的问题：给定$r_i$，求排列的个数。

这个问题很好解决：把$r$排序，然后答案就是$\prod_i (r_i-i)$。

但是有限制呢？考虑容斥，用$\le r$的减去$<l$的。

然而这样可能就会对排名产生一些影响，从而不太好统计答案。

发现$l_i\ne 0$的$r$必然大于$l_i=0$的$r$，而且$l_i\ne 0$的时候$r$随着$l$增大而增大。

于是可以枚举有几个位置选了$<l$的，然后就可以每次插入一个点的时候求出它的排名了。

不知道为什么细节就是很多……

ARC071E TrBBnsformBBtion

注意到经过操作可以使ab变成ba，于是顺序不重要了。

注意到aa和b可以互相转换，于是可以把两个串都变成只有a的形式，答案不变。

注意到如果原来长度模3余数不同，那么乘2之后也不会相同，所以直接判长度模3是否相同即可。

ARC071F Infinite Sequence

显然数列会是11121113111111151111112112222...这样，只是最后边界会有一些细节。

设$dp_n$表示长度为$n$，最后给够了1，的方案数，那么就有$dp_n=\sum_{i=0}^{n-1} dp_i-dp_{n-2}$。

统计答案的时候分类讨论：最后是1且给够了；最后是1且没给够；最后不是1。

ARC072D Alice&Brown

打表找规律，发现$|x-y|\le 1$的时候先手输，否则先手赢。

证明什么的归纳一下就好了，就是不知道如果不打表怎么想出来……

ARC072E Alice in linear land

推错了一个地方，离正解就差一点点……

处理出用前$i$个会走到距离$dis$，然后发现改变之后距离可以是$[0,dis]$中的任意一个。

所以我们就要处理出每个后缀可以搞出的从0开始的距离区间。

发现只要有一个搞不出来，那么后面的都废了。

于是随便递推一下，就做完了。

ARC072F Dam

神仙题？

首先可以把水看做二元组$(V,V\times t)$，那么混合的时候可以直接相加。

维护一个水的单调队列，里面温度单调上升。

新加一些水的时候，如果水坝满了，那么显然放掉最前面的更优。

然后如果当前水比队尾的水温度低，那么如果后面要放水，肯定是要先混合再放水，所以一直往前混合直到当前水比队尾水温度高，这样也满足了单调性。

ARC073E Ball Coloring

看错题，做得我一脸懵逼？

考虑最大值和最小值是否在一个集合。

如果最大值为红，最小值为蓝，那么直接所有较大的设为红较小的设为蓝即可。

如果最大最小值都为红，那么把剩下的集合按较大的元素排序，枚举蓝色集合的最大值，搞一搞答案。

（我看不懂网上题解，又懒得写代码，所以这个可能是错的，但我觉得这题乱搞就完事了）

ARC073F Many Moves

做了不知道多少遍的套路题……

设$dp_{i,j}$表示昨晚前$i$个，一个在$a_i$处，另一个在$j$处，的最小值，暴力转移是$O(qn)$的。

发现可以线段树优化一下，没了。

ARC074E RGB Sequence

设$dp_{i,j,k,0/1/2}$表示做完了前$i$个，第$i$个的颜色是红/绿/蓝，另外两种颜色最后出现的位置是$j,k$的方案数，每次在右端点处处理不合法的情况，直接删掉就好了。

ARC074F Lotus Leaves

容易想到最小割，但普通建图是$O(nm)$的，大概过不了吧？

考虑一行一列随便跳，那么给行列建点，一片荷叶就是连接行列，此时点数就是$O(n)$的了。

ARC075F Mirrored

这场只有F的原因是前几题都没啥意思……

考虑把$rev(n)=D+n$写成竖式的形式，枚举$n$的位数（可以发现位数最多是$D$的两倍），发现确定了最后$k$位就可以确定前$k$位，也就是一个对称着确定的形式。

但有一个东西叫做进位比较麻烦，所以我们设$dp_{i,0/1,0/1}$表示做了低位的$i$位，第$i$位是否会给$i+1$位进位，第$len-i$位是否需要给第$len-i+1$位进位，的方案数，然后枚举某一位填什么来转移。（状态可能有一些加一减一不太对，不管了）

最后还要根据$len$的奇偶性分类讨论一下，感觉挺麻烦的，于是代码咕了/cy。

ARC076F Exhausted?

你很容易发现这是个求二分图最大匹配，你也很容易发现暴力建图会T。

想到前后缀优化建图，但这样复杂度就不是$m\sqrt n$了。鉴于网上没有题解这么写，我们就当它过不了好了。

那么怎么办呢？考虑霍尔定理：二分图有完美匹配的充要条件是对于左边任意一个集合$X$，记$w(X)$表示$X$能连到的右边的集合，都有$|X|\le w(X)$。

我们加$k$把椅子，显然会使得$w(X)$变大$k$，也就是要满足对于任意$X$都有$|X|\le |w(x)|+k$，即$k\ge \max(|X|-|w(X)|)$。

由于边的特殊性，$|X|-|w(X)|=|X|-m+\max(\max R-\min L-1,0)$。

显然$\max R-\min L-1<0$的时候取$X=\{1,2,...,n\}$最优，所以可以把$\max$删掉。

然后枚举一下$\max R$，线段树维护$|X|-\min L$的最大值即可。

ARC077F SS

设初始给的串是$SS$，那么我们只关心$S$的变化情况。

如果$S$本身有循环节$len,len|n$，那么容易发现$f(S)$就是多加一个循环节到后面，我们特判掉。

否则，设$T$为$S$长度为$n-nxt_n$的前缀，可以发现$S$的变化情况就是$S\to ST\to STS\to STSST\to STSSTSTS\to \cdots$。

找规律得第$i$个串就是第$i-1$个串拼上第$i-2$个串。证明我就不会了……

串的长度是$fib$数列，所以很快就可以爆$10^{18}$，于是可以设$f_{i,c}$表示第$i$个串$c$的出现次数，递推搞出来。

统计答案的时候先差分，然后可以拆成好多个串拼在一起，就做完了。

ARC078E Awkward Response

注意到这个询问的方式唯一有点恶心的就是有一个按字典序比较的限制，考虑去掉它。

你发现只需要确定$n$的位数就可以二分了。

位数怎么确定？你询问$10^k$，一般来说他会返回$[n>10^k]$。

什么时候会有特殊情况？$n$自己就是10的幂，这时他永远返回1。

于是你问一下$10^{10}$判一下是否是特殊情况，如果是就问一下$10^k+1$，否则二分$n$的位数再二分$n$就没了。

ARC078F Mole and Abandoned Mine

之前写过了，见上。

ARC079D Decrease (Contestant ver.)

有趣的构造题。

一开始我看错题了，以为$k\le 10^{16}$，于是就想了个$n=2$的解：

考虑$(a,a)$，他会经过这样的变化：$(a,a)\to (a-2,a+1)\to (a-1,a-1)$，也就是经过2步使得两个数减1。

那么$k$为奇数怎么做呢？考虑$(a+3,a)$，他会经过这样的变化：$(a+3,a)\to(a+1,a+1)$，经过1步之后变成上面那个形式。

这样在$k$较小的时候没有问题，但$k>2\times 10^{16}$时就不能这样做了。

考虑扩展一下，发现$n$个$a$会经过$n$步之后变成$n$个$a-1$，所以只需要搞一搞余数。

我们令第一个数为$a+n+1$，于是经过1步后变成了$n$个$a+1$。所以只需要给第一个数加上若干个$n+1$，再给所有数减若干个1，就可以把余数表示出来。

然后你发现$n\times n>10^3$，你被卡了。感性理解一下，发现加$n+1$的操作好像可以加到任意一个数，于是做完了。

（$k$较小的时候这么做可能会有一些边界情况，此时用$n=2$的更保险）

ARC079E Decrease (Judge ver.)

这题就没什么意思了，每次把最大的模$n$，贡献加到其他数上，感性理解没什么问题。

应该就是因为操作的顺序不太重要，所以可以先对着一个数搞到小于$n$再搞其他的。

ARC079F Namori Grundy

咋回事啊？怎么F还没D有趣啊？

显然给的图是个基环外向树，显然树上的情况是确定的，只需要对环进行一些调整。

先对每一棵树dfs，得到环上的结果，设为$a_i$。这里的$a_i$不是最终结果，可能会由于环上数值的冲突而变大。

先判一下是否所有$a_i$均相等，如果是，那么容易发现偶环有解，奇环无解。

否则，考虑相邻两个相等的$a_i$，此时需要把前一个$a_i$加1……一直这样做就一定有解？

错了，你发现后面那个$a$可能会变大，于是前面这个不用变，于是比较恶心。

注意到一定会存在连续的两个$a_i$，使得前面的小于后面的。这时后面的怎么变大都不会影响前面这个$a_i$，于是断环为链，肯定有解。

又因为没有输出方案，所以你用十分不严谨的思路得到的答案也是对的……

ARC080F Prime Flip

日常想不到差分，我菜死了……

差分之后仍然只会有$O(n)$个点是1，并且每一次操作变成翻转$x,x+p$，目标状态是全0。

感性理解，没有目的地把0翻成1是没有用的，于是只有下面三种操作：

$|x-y|=p$，此时只需一步。
$|x-y|$为偶数，根据哥德巴赫猜想，需要两步。（2，4特殊，但$2=5-3,4=7-3$）
$|x-y|$为奇数且不为质数，此时可以先搞成偶数再用两步，一共3步。

发现最优解是用尽量多的1操作，然后再用2，最后用3。

1操作里的$x,y$奇偶性不同，所以搞个二分图匹配就没了。

ARC081F Flip and Rectangles

不知道怎么就注意到了一个性质：如果一个矩形里面不存在有奇数个1的$2\times 2$的子矩阵，那么它就可以变成1。

为什么？显然，无论怎样变换都不会改变奇偶性，所以必要性有了。而如果你用列操作把第一行做成了全1，那么用奇偶性推一推就可以看出此时每一行的值都相同了。

然后就变成类似于最大子矩阵的东西，单调栈即可。

ARC082E ConvexScore

首先，你不能像我一样看错题……

看到$2^{n-|S|}$，容易想到子集个数。

于是可以想到枚举点集，然后贡献到这个点集的凸包上。

于是就转化成有多少个点集存在凸包，改成多少个点集没有凸包，然后就很好做了。

ARC082F Sandglass

考虑每一次翻转中间的过程，要么是$x\to \min(x+t,X)$，要么是$x\to \max(x-t,0)$。

我们还发现一个性质：初始沙子越多，最后剩的越多。

于是就是一个一次函数向上敲一敲，向下敲一敲，肯定会变成两边平中间一个斜坡的样子。

ARC083F Collecting Balls

首先看到网格图，依据你对atcoder的理解，应该可以想到行列连边。

然后发现对于每个连通块，由于每个点必须删掉一条边，所以必然$m=n$，即一棵基环树。

对于树边，显然点和边的对应关系是确定的。我们枚举环上是顺时针还是逆时针，然后考虑删除的先后关系有什么要求。

如果$x$要删除$(x,y)$的点，那么对于所有$(x,k),k<y$，都必须先删掉，所以$k$要比$x$先动。据此可以连出一个DAG。

可以发现，每个点的出度必然是0或1，并且连向的点是连通块里的点（于是每个连通块就是独立的了），所以每个连通块都可以连出一个内向森林。

于是每个连通块分别做出答案再合到一起就没了。

ARC084D Small Multiple

这都不会，丢人现场.jpg

你很容易往数论上面想，然而你建出$[0,K-1]$的点之后枚举$x\to x\times 10+y,y\in[0,9]$，把边建出来就做完了……

ARC084E Finite Encyclopedia of Integer Sequences

当$k$是偶数的时候容易想到$\{k/2,k,k,k,k,k,k,\cdots\}$是最终答案。

当$k$是奇数的时候，我们先令$B=\{\lceil k/2\rceil,\lceil k/2\rceil,\cdots\}$。

定义$f(X)$为一个对数列进行的操作，使$X_i\to K+1-X_i$。

可以发现，这几乎可以使得小于$B$的数列和大于$B$的数列一一对应，只有$B$的前缀例外。

于是可以知道$B$比答案只大了$n/2$（可能有+1-1），暴力退回去即可。

ARC084F XorShift

可以想象线性基的过程，也可以想象多项式$\gcd$的过程，先把所有数都合并成一个，然后考虑最后剩下的数能组成的小于等于$X$的数的个数。

设$X$长度为$b$，最后剩下的是$a$，那么显然前$b-a+1$位随便乱填之后可以唯一对应到一种组合方法。

然而如果前面填的和$X$相同，那么最后可能会超出范围，所以还要特判一下。

AGC030C Coloring Torus

容易想到一种$n=K$的构造方法：每行都放同一个数。这显然是合法的，但$K>500$时就失效了。

每行交替放两个数？画一画会发现只对$4|K$的时候有效，似乎没什么前途。

我们尝试每条对角线交替放两个数，如果$K$为奇数就有一条对角线只放一个数。可以发现，这样在矩阵无限延伸的时候一定是合法的，但要框出一个$n\times n$的矩阵就不一定合法。

但我们又发现，只要$2|n$就合法，而$2|\frac{1000}{2}$，所以这样是没问题的。

确定了$n$之后解方程可以算出有$2n-K$条对角线是只有一个数。注意特判边界情况。

ARC103D Robot Arms

不管怎样还是要想到二进制拆分的。

为了证明无解，要注意到凑出的两个数的和必然是奇偶性相同的，否则无解。

我的垃圾想法：把两个数看做独立的，分别用一些数去凑它。使用$1,2,4,...,2^{30}$来凑一个数。虽然每个数都必须要用，但注意到可以用$1,2,4,8,...$来凑出一个1，所以问题不大。

然而这样就要用60个数，就死了。

正解：不把两个数看做独立的，使用归纳法把一整个斜正方形的点都凑出来。膜 https://blog.csdn.net/zxyoi_dreamer/article/details/82905515

ABC134F Permutation Oddness

很好，这篇博客连abc也有了……这是我越学越菜的表现吗？

发现如果从小到大填数或是从小到大确定位置都要面临状压的命运，所以都不行。

所以我们两个一起填（？？？）。

设$dp_{i,j,k}$表示已经搞了前$i$个位置和数，还有$j$个没有被匹配，当前已经确定的贡献是$k$，的方案数。

由于已经确定某些位置/数没有被小于等于$i$的匹配，所以它的贡献已经确定了，所以不再有状压的必要。

AGC041F Histogram Rooks

疯狂容斥……

容斥0：枚举哪些格子没有被覆盖，然后对于一个位置如果行列都没有被钦定未被覆盖的格子，那么方案数是 2 。

显然这个容斥的复杂度非常爆炸，而且也不是很好 DP 。

容斥1：枚举哪些列里面有格子被钦定未被覆盖，那么这些列都不能放棋子了。设集合为 $S$ 。

那么此时考虑一个极长行连续段的贡献，假设里面有 $p$ 个格子在 $S$ 里，那么贡献有两种：

这 $p$ 个格子都没有钦定未覆盖，所以剩下的格子可以随便放，方案数 $2^{len-p}$ 。
枚举里面有几个格子被钦定，方案数是 $\sum\limits_{i=1}^{p} {p\choose i}(-1)^i=-[p\ne 0]$ 。

但是这样算出来的结果仍然是错的，因为某一些在 $S$ 里的列可能还是没有钦定的格子。

容斥2：在容斥1的基础上再套一个容斥，枚举集合 $T\subseteq S$ ，表示 $T$ 里面没有被钦定的格子。

设一个极长行连续段里面有 $q$ 个格子在 $T$ 里面，那么第二种的贡献变成了 $-[p\ne q]$ 。

注意到此时贡献只和 $p,[p\ne q]$ 有关，所以 DP 的状态数可能不会太大，来尝试设计一个 DP 。

每次从 $h$ 最小的位置切开来，下面会形成一个矩形，上面会被分裂成一些子问题，并且子问题形成树形结构，并且矩形里的行连续段的 $p,q$ 就是由上面的加起来，再算上独有的列。

于是可以设 $dp_{x,p,0/1}$ ，$p$ 表示 $S$ 的大小，$0/1$ 表示是否有 $p\ne q$ 。

转移就是无脑从儿子用背包合并过来。对于独有的列也可以看做是一个特殊的儿子。

然后此时每一行的方案数都是相同的，直接快速幂即可。

复杂度 $O(n^2\log n)$ ，预处理一些东西可以变成 $O(n^2)$ 。

AGC043C Giant Graph

注意到一个性质：对于相邻的两个点，它们的权值一定不同。

也就是说权值相同的点之间一定没有边。

所以有一个很显然的贪心：无脑选权值最大的点。

（我这都没想到？？？）

那么把边定向，从权值小的连向权值大的，会变成一个 DAG 。

此时一个点会被选当且仅当它连向的点都没有被选。

可以发现这个东西很像博弈论的图，我们要的答案就是所有必败态的权值之和。

而由于每走一步都只是在某一个图里面走，所以相当于三个子游戏，可以把三个图分开求 SG 值，然后答案就是 $f_A(x)\oplus f_B(y)\oplus f_C(z)=0$ 的点 $(x,y,z)$ 的权值和。

注意到 $f(x)$ 的值域是 $O(\sqrt m)$ 的，所以统计答案的时候暴力即可。

AGC043D Merge Triplets

Atcoder 日常 D 比 C 水……

显然造排列的方式就是归并排序，而归并排序的性质：把每一个序列按前缀最大值分成若干段，然后把段按段头的大小排序。

所以判断一个序列合法的方式：从第一个开始，每次把比段头小的数全部加入这一段。那么合法当且仅当每一段长度不超过 3 ，且 2 的个数小于等于 1 的个数。

设 $f_{i,j}$ 表示把 $i$ 个数分成若干段，使得 1 的个数减 2 的个数是 $j$ ，的方案数。由于最大的那个数一定是最后一段的段头，所以枚举它所在的段的长度是 1/2/3 即可转移。

AGC044D Guess the Password

我菜炸了 /kk

性质 1 ：询问一个长度 128 的由字符 $c$ 组成的串，即可得到原串里有几个 $c$ 。

很容易构造出方法。

性质 2 ：很容易求出一个串是否是原串的子序列。

根据这两个性质即可合并两个已知顺序的字符集合：把 $x$ 往 $y$ 的序列里面挨个插入，即可知道它们的相对顺序。

于是每次合并两个最少的字符，即可做到 $O(L\log L+|\Sigma|)$ 。

AGC044E Random Pawn

果然我只会做套路题 /kk

考虑 $a$ 最大的位置，显然如果走到它就不会再动了，所以可以从这里切开，变成序列。

然后设 $f$ 为答案，则有 $f_i=\max(a_i,-b_i+\frac 1 2(f_{i-1}+f_{i+1}))$ 。

没有 $b$ 的版本我们是会做的（[USACO18DEC]Balance Beam P），所以尝试把 $b$ 消掉。

给每一个位置弄一个 $k_i$ ，令 $g_i=f_i+k_i$ ，且 $g_i=\max(a_i+k_i,\frac 1 2(g_{i-1}+g_{i+1}))$ 。

可以得到一些关于 $k$ 的方程，并且用线性消元的方法可以解出一组解。

然后求凸包即可。

AGC045D Lamps and Buttons

不会做套路题了 /ll /dk

显然可以枚举前 $A$ 个位置中第一个自环在哪里，然后容斥一下使得这真的是第一个自环，然后就是有一个三元组 $(x,y,z)$ ，要求有多少个 $x+y+z$ 的排列，使得 $[x+1,x+y]$ 的点所在的环中至少有一个 $[1,x]$ 的点。

可以先用 $x!$ 得到前 $x$ 个点在环中的相对顺序，然后对于后面 $y$ 个点，第 $i$ 个点可以插到 $x+i-1$ 个点的后面，然后 $z$ 个点随便放。

所以答案就是 $(x+y+z)!\times {x\over x+y}$ 。

AGC045E Fragile Balls

没啥思路，于是建图，连边 $(A_i,B_i,C_i)$ ，其中 $C_i$ 为边权。

缩点，那么会得到一个 DAG 。先不考虑最小化步数。

考虑对于一个强连通块（如果非简单环），一定可以做到每一个球都一步走完：无脑走，最后如果出现了简单环，那么可以在这个环上的另一条边走掉之前把这一整个环给走掉。

所以对于一个弱连通块，只要不是简单环，都可以使得所有不在目的地的球一步走到。（注意由于保证了每个点都有入度，所以非简单环时球数一定大于点数）

对于一个简单环，需要一个球冲进来，把一整个环走掉，然后再把这个球送走。

然后就是大力分类讨论了……可以把弱连通块分为三种。

仅自环。（只有一条边）
仅简单环。（同样不能有重边）
其他所有弱连通块。

设 “费用” 表示除了 $\sum [a_i\ne b_i]$ 之外的步数。为了计算费用可能会把多余步数贡献到跳的球或被跳到的点上。

以下基本不再区分球和点。

对于一类块，如果有点进来，那么它可以跳出去进行操作再跳回来，可以贡献 $c-1$ 次移动，额外费用是 2 （自己跳回来一步，别人跳过来一步）。

对于二类块，显然必须有点进来，那么一个点可以在走到 $B_i$ 之前先跳出去进行操作，然后直接跳到 $B_i$ ，所以一共贡献 $\sum (c_i-1)$ 次操作，额外费用是 1 （别人跳过来一步）。

对于三类块中的非自环，可以贡献 $c_i-1$ 次操作，额外费用是 0 。

对于三类块中的自环，可以贡献 $c_i-1$ 次操作，额外费用是 1 （自己跳回来一步）。

显然应该优先用三类块中的非自环球，然后用二类的球，然后用三类的自环球，最后用一类球。

设一类用了 $X$ 个，二类有 $Y$ 个，那么需要总贡献 $\ge X+Y$ ，额外费用为 $2X+Y+三类块中用的自环个数$ 。并且如果 $X+Y\ne 0$ 那么三类贡献必须非 0 。

瞎搞搞即可。

AGC045F Division into Multiples

首先把 $A,B,C$ 搞成两两互质的。

设 $g=\gcd(A,B)$ ，那么 $A/=g,B/=g,C/=\gcd(C,g)$ 。

然后假设 $\gcd(A,C)=k$ ，那么显然一个集合中的 $B$ 加起来也要是 $k$ 的倍数，而 $\gcd(k,B)=1$ ，所以可以 $Y/=k,A/=k,C/=k$ 。对 $B$ 也类似的方法做一下。

最后特判此时 $C=1$ 。

现在我们就不必考虑一些奇怪的情况了。

考虑所有有用的二元组 $(x,y)$ 满足 $C|(xA+yB)$ ，显然 $x$ 递增 $y$ 递减。怎么找到它们呢？

设 $D={A\over B}\pmod C$ ，那么二元组就变成了 $(x,C-xD)\pmod C$ 。

所以就是要找到 $(x,xD)$ 两维递增的 $x$ 。

构造一个长为 $C$ 高为 $D$ 的循环网格，从 $(0,0)$ 开始往右上方走，每次走到顶端且横坐标比以前都大，就把此时的横坐标记下来，作为 $xD$ ，而 $x$ 就是碰到上边界的次数。还要把 $(0,0)$ 给记下来。

考虑第一次会记一个 $(D,D)$ ，那么可以把左边那个正方形直接删掉，因为从正方形的某个地方出发这么走其实相当于平移到另一边，而在这其中碰到的上边界我们不关心。

所以设此时的网格为 $(W,H)$ ，然后类似欧几里得的做。

这样可以发现，找到的 $(x,C-xD)$ （记为 $(x,y)$）两维都可以被分成 $\log$ 个等差数列，并且是有凸性的：$x_{i}-x_{i-1} \leq x_{i+1}-x_{i}, y_{i-1}-y_{i} \geq y_{i}-y_{i+1}$ 。

移项，即可得到性质：选出来的 $(x,y)$ 只会是相邻的两项各拿一些。

所以二分答案，然后枚举每个等差数列来判断是否合法。既然是等差数列那就随便判了。

AGC046D Secret Passage

好像有各种神奇做法。

显然，一个字符如果经历了被选中的过程而没有被删，那么它的位置已经可以随便丢了。

考虑倒推一个字符串 $t$ 是否合法：贪心求出 $s$ 最长的后缀，使得它是 $t$ 的子序列，那么 $t$ 中没有被匹配的位置就是需要前面被甩过来的字符。

所以可以枚举一个前缀，算出这个前缀处理掉之后能往后丢哪些字符集，然后用组合数算一下把这些字符往后塞的方案数，使得匹配恰好是匹配到那个后缀即可。

往后丢的字符集简单 DP 一下即可。有一些奇奇怪怪的细节。

AGC046E Permutation Cover

考虑什么时候有解：$2\min\ge \max$ 。容易证明是必要条件，充分性可以用构造来说明：https://atcoder.jp/contests/agc046/submissions/15408360

但是为什么 WA 了呢？因为我没看到要字典序最小……

字典序最小自然考虑贪心。考虑这样加字符：一次加长度 $\le K$ 的一段，每次加完之后保证最后 $K$ 个是一个排列，并且不存在加这个段的前缀使得最后 $K$ 个是排列的方案。显然所有合法的序列都可以用这个方法构造出来。

先考虑对于一个需要被加入的次数 $b$ ，和原来结尾的一个排列 $p$ ，怎样判断合法。

显然还是需要 $2\min+1\ge \max$ ，而 $2\min+1=\max$ 的时候需要在 $p$ 中，取到 $\max$ 的字符出现位置都比 $\min$ 的出现位置小。同样可以比较容易地发现这是充要条件。

然后思考怎么一次加一段使得后面合法且这个段字典序最小。

枚举这一段的长度 $len$ ，就可以确定加入的字符是哪些。对于这些字符，可以一个一个尝试加入最小的字符，然后判断后面是否合法。

怎么判是否合法呢？显然这一段中还没有被加入的字符应该按照后面出现次数从大到小加入，然后暴力用上面的方法判后面是否合法即可。

复杂度大概是对的吧，不想算了。

World Tour Finals 2019 C Triangular Lamps

好妙啊 /kk

首先，在不考虑复杂度的时候，想一想怎么确定一个点。

把所有点往下推（或者往任意一个方向推），推到一条直线上，那么可以证明起始点固定的时候这条直线上的图案是固定的。

为什么呢？考虑如果两个不同，那么两个异或一下，就相当于从空坐标系开始操作，要使得黑点全都在一条直线上，可以发现这是不可能的。

所以选择从起始点无脑推到这条直线上，只需要确定直线上最靠两边的两个点的位置，就可以确定起始点的位置。

考虑直线上的图案是怎样的，每一层叠起来会形成一个 Sierpiński_triangle ，第 $i$ 层的第 $j$ 个是 1 当且仅当 ${i\choose j}$ 不被 2 整除，即 $i\&j=j$ 。

所以用 lucas 定理即可在 $O(n)$ 的时间内求出一个点是否为 1 （考虑每个点的贡献即可）。

而观察这个 Sierpiński_triangle 的性质，发现只要能确定一个 1 ，就可以倍增往两边跳，得到两边的 1 ，所以问题转化为求一个 1 。

当起始点在 $x$ 轴上时，选择直线 $x+y=c$ ，那么 $(c,0)$ 一定是 1 。

对于其他时候，我们要找到更加强且更加神仙的性质。

这个三角形满足这样一个性质：每一层的点按编号模 3 分类，那么一定有一类的 1 的个数是奇数。证明可以从一开始 $cnt_0=1,cnt_1=cnt_2=0$ 开始归纳。

既然是奇数那么就可以二分，问题转化为求 $x\in[l,r],x\equiv p \pmod 3$ 的黑点个数的奇偶性。由于只关心奇偶性，所以可以对于每一个初始的点分别做数位 DP 。

最后复杂度 $O(n\log^2 MAX)$ 。

AGC047F Rooks

你以为你要推一堆性质，但其实并不能推出什么性质。~~然而还是看着题解推了一下午~~

先把横纵坐标分别离散化成排列。

显然任意时刻 King 的移动范围都是一个矩形，并且矩形内横纵坐标都连续。把点按横坐标排序后这样的矩形就对应到一个连续段。

直接设 $dp_{l,r,0/1}$ 表示吃掉了 $[l,r]$ ，现在在 $l/r$ ，剩下的答案。转移就枚举下一个吃哪边。答案就是 $dp_{i,i}$ 。复杂度 $O(n^2)$ 。

考虑如果一个区间 $[l,r]$ 是一个连续段并且有序，那么吃了 $l$ 之后一定会一路吃到 $r$ ，吃了 $r$ 同理，所以 DP 的时候吃掉一个就可以吃掉一段。

考虑直接从每个 $dp_{i,i,0}$ 开始记忆化搜索，复杂度和能走到的状态数有关。定义一个区间合法，当且仅当它是连续段，并且可以通过删掉两边的 $\max/\min$ 最终删成空。显然能走到的状态就是合法区间个数。

先找到一个性质：把一个排列中所有合法区间拿出来，删掉被覆盖的，那么剩下的区间不会覆盖一个位置三次以上，即不存在三个极长合法区间两两有交。证明可以反证，用连续段的一些性质证明其中一个必定不是极长的。

再找到一个性质：如果一个合法区间覆盖另一个合法区间，那么要么从大的开始删可以删成小的，要么小的是有序的。证明同样可以反证，比较简单。

设 $S_{l,r}$ 表示 $[l,r]$ 通过删两边可以走到的合法区间数，$Sl_{l,r}$ 表示以 $l$ 为左端点的合法区间数， $Sr_{l,r}$ 同理。尝试证明当 $[l,r]$ 是合法区间时 $S_{l,r}=O(r-l)$ 。如果可以证明这个，那么再根据上面那个性质，把所有极长合法区间的 $S$ 加起来，就可以证明所有能到达的状态是 $O(n)$ 的。

如果 $l,r$ 分别是区间中的最小最大值，那么 $S_{l,r}=S_{l+1,r-1}+Sl_{l,r-1}+Sr_{l+1,r}+1$ 。不妨设 $y_l$ 是最小值， $y_r$ 是最大值。先把从 $l$ 开始的连续上升段和在 $r$ 结束的连续下降段缩成一个点。考虑 $y_{l}+1$ 的位置，如果是 $r-1$ 那么显然有 $Sl_{l,r-1}=2$ ，否则 $y_{l+1},y_{r-1}$ 都不是 $[l+1,r-1]$ 的最小值，那么为了让 $[l,r]$ 合法，就必须有 $y_{l+1}=y_r-1$ 。此时也容易看出 $Sl_{l,r-1}=2$ 。 $Sr_{l+1,r}$ 同理。

否则，不妨假设 $r$ 不是，而 $y_l$ 是最小值。则此时 $S_{l,r}=S_{l+1,r}+1$ ，显然是 $O(r-l)$ 的。

然后终于证明完了。代码只需要冲一个记忆化搜索即可。

AGC048D Pocky Game

orz 想不出来 /kk

$n$ 很小，而删东西是两边往中间走，所以考虑区间 DP 。

注意到一次操作如果没有删完，那么显然 -1 是最优的。

从一个区间走到另一个区间时，一定是某个元素被删掉了，但另一边的元素可能不是原来的样子了，不好处理。

但是显然这个元素越大就对这边的人越有利。所以设 $f_{i,j}$ 表示只剩 $[i,j]$ ，假设 $a_i$ 可以任意取，左边人先手，需要 $a_i$ 多大才能赢。 $g_{i,j}$ 就是右边人先手， $a_j$ 任意取。

如何转移？如果直接删掉 $a_i$ 就能赢那么 $f_{i,j}=1$ ，否则会用 $a_i$ 和 $a_j$ 拼点，直到减到某个阈值时会把 $a_i$ 或 $a_j$ 删掉，转移式大概是 $f_{i,j}=a_j-g_{i+1,j}+1+f_{i,j-1}$ 。

AGC048E Strange Relation

先考虑怎样求出字典序最大的 $\{x_i\}$ ：从 1 开始，每次先把 $x_i$ 置为 $i-1$ ，然后可能 $x_i$ 大了，就要减 1 ，一直减到恰好相等。显然不会减到负。所以不妨先让 $a_i=a_i+(i-1)T$ ，然后减若干次直到合法。现在设减的次数为 $x_i$ ， $c_i=a_i-x_iT$ ，那么 $x_i$ 就是 $c_j\ge c_i,j<i$ 的 $j$ 的个数。

直接用贪心的思路显然是没有前途的。考虑如果把 $a_1$ 删掉，后面的 $c$ 会怎么变。发现 $c_i\le a_1$ 的会加上 $T$ ，然后就没有变化了。这个结论很容易证明，大概是考虑 $c_i>a_1$ 的 $c$ 不会变化，而 $c_i\le a_1$ 的一起加，所有 $c$ 的相对大小全都不变，且 $c_i\le a_1$ 的加完 $T$ 后还是 $\le a_1$。

然后考虑怎么求出一个位置最终的 $c$ 。容易想到用上面的方法倒推回去，维护当前的 $c$ 。每考虑一个 $a_i$ ，如果 $a_i$ 较小就不变，否则 $c=c-T$ 。

然后 DP 就很显然了。

ARC106E Medals

显然可以二分答案。显然答案是 $O(nk)$ 级别。

注意到 $n$ 非常小，考虑 Hall 定理。发现 $n$ 也非常小，所以直接 FMT 解决。

ARC106F Figures

显然考虑 prufer 序列，随便推推生成函数，发现答案就是

\[\left(\prod a_i\right)\left(\sum (a_i-1)\right)^{\underline{n-2}} \]

ARC107E Mex Mat

打个表发现主对角线基本上是一样的？

先证明 0 的传递性，然后证明 1 的，然后证明 2 的，就做完了。

ARC107F Sum of Abs

被网络流打傻了，明明知道是网络流但还是不知道怎么搞……

由于绝对值的符号搞反只会使得结果变小，所以把问题转化为给每个点一个 $\{-1,1,0\}$ 的种类，表示权值为 -1,1 或是被删除。那么限制就是权值为 -1 和 1 的不能有边相邻。~~我这步都没想到可以退役了~~

然后考虑用最小割来处理代价。建图也非常神仙，不知道怎么想出来的。

一个点拆成两个 $X_i,Y_i$ ，连边 $(Y_i,X_i,\infty^2)$ 。那么一个割只会对应到三种情况中的一个： $(X=S,Y=S),(X=S,Y=T),(X=T,Y=T)$ 。三种情况分别对应到三种代价，并且限制也可以用 $\infty^2$ 的边权表示。为了使得不存在一个点与 $S,T$ 都不相连，需要把普通边的边权全部加上 $\infty$ 。

AGC049D Convex Sequence

先让所有 $a_i$ 减去 $\min a$ ，最后加回去，那么变成统计 $\sum\le m$ 且模 $m$ 同余的方案数。由于凸性，此时非 0 的数只有 $O(\sqrt m)$ 个。

先假设 $a$ 单调不降。为了处理凸性，可以考虑 $\Delta a_1$ 和 $\Delta^2 a_i$ 的贡献，然后大力背包。先把每个 $n'\le n$ 的背包都做出来。

先考虑 $n$ 比较小的情况，即 $n=O(\sqrt m)$ 。直接枚举第一个 0 在哪里，然后合并两个背包。

否则不管非 0 的数有几个， $n$ 一定是够大的，所以直接无脑合并背包即可。

正解根本不需要考虑那么多破事，所以我又做麻烦了……

AGC049E Increment Decrement

一个没怎么看懂的做法

考虑一个序列怎么做。发现没有什么贪心做法，也没看出什么性质，所以只能直接冲 DP 。

由于操作可逆，换成把 $A$ 变成 0 。先单点操作，再区间操作。设单点操作之后得到的序列为 $B$ ，那么区间操作的代价就是 $C\sum |B_i-B_{i-1}|/2$ 。此处不选择 $\max(B_i-B_{i-1},0)$ 是因为这个不优美。

然后冲 DP ：设 $dp_{i,j}$ 表示确定了前 $i$ 个， $B_i=j$ ，的最小代价。转移为

\[dp_{i,j}=2|A_i-j|+\min_k \{ C|j-k|+dp_{i-1,k} \} \]

（为了方便，代价乘了 2 ）

然后由于 $2|a_i-j|$ 是凸的，所以尝试归纳证明 $dp_i$ 是关于 $j$ 的下凸函数。考虑后面那个东西，相当于把斜率绝对值大于 $C$ 的掰成 $C$ ，而前面的就是给前缀斜率减 2 ，后缀斜率加 2 。初始 $dp_{0,0}=0$ ，斜率为 $\infty$ ；答案为 $dp_{n+1,0}$ 。

然后考虑每次操作对 $dp_{i,0}$ 的贡献，就得到这么一个算法：维护一个集合 $S$ ，初始有 $C$ 个 0 。每次加入两个 $A_i$ 并给答案加上 $A_i$ ，然后把 $\max,\min$ 从 $S$ 中删去，并给答案减去 $\min$ 。

$\min=\sum_{i} [\min>i]$ ，而集合中也只和大小关系有关，所以考虑每个 $i$ 的贡献即可计数。

ARC108E Random IS

无脑区间 DP ： $dp_{l,r}$ 表示已经选了 $l,r$ ，中间的期望贡献。显然枚举中间下一个被选的点之后两边独立。暴力做是 $O(n^3)$ 。

从左往右枚举 $r$ ，从右往左枚举 $l$ ，用数据结构加速转移即可。更具体地，枚举 $l$ 时树状数组维护已经走过的点的 DP 值，以及对于每个 $l$ 用树状数组维护 $dp_{l,r}$ 。那么转移的时候就区间查询值域在 $[p_l,p_r]$ 的点即可。

ARC108F Paint Tree

枚举直径端点的颜色。如果直径端点同色那就随便搞，所以考虑异色的情况。

此时分析一下会发现，每个点在同色点里的最远点一定有一个是原来的直径端点。于是每个点会有两个权值 $w_0,w_1$ ，分别表示取黑色和白色的最远点对距离。

考虑每个 $w$ 的贡献即可。也有更巧妙的方法，但不重要了。

感觉这场 arc 难度不太行啊？

ARC109E 1D Reversi Builder

先考虑最优策略会怎么操作。

显然在任意时刻，已经存在的石子一定是左边黑右边白，或是相反。

注意到如果两端同色那么最终也一定同色，所以考虑两端异色的情况。不妨设左边是一堆白，然后出现一个黑，右边相反。

那么如果左边的黑先被拿到，执白者就可以再拿一个白，这样到右边的白被拿到时就会中间全部变成白色了。

所以最优策略就是往自己那一边拿，谁先拿到对方的最后一个谁就赢。

计数随便搞搞吧。

ARC109F 1D Kingdom Builder

考虑对于最终选出来的一组位置，怎样才能使它们合法。

显然只需要让每一段都有至少一个被点亮就可以合法。设最后被点亮的段点亮的第一个颜色为 $c$ ，那么除了最后一段以外其他段都要先加到两边不是 $c$ 为止。设点亮最后一个段的 $c$ 时其他段目前加入的部分为关键段，那么显然只会对关键段有限制。

那么第一个显然的限制是：除了最后一个关键段，其他关键段都要满足两侧的字符不是 $c$ 。

由于最后一个加入的是 $c$ ，那么其他关键段中只要存在 $c$ ，也就可以在最后一个之前加入。剩下的关键段内部没有 $c$ ，两侧也没有 $c$ ，所以只能有一个，它必须是第一个。

所以就是三个条件：

最后一个关键段中间有 $c$ 。
中间的关键段两侧没有 $c$ ，且中间有 $c$ 。
第一个关键段两侧没有 $c$ 。

从关键段扩展到整段，从而包含所有要求的位置，是不难的。

所以可以记录一万个状态做线性 dp ，就做完了。

ARC110F Esoswap

下面不区分 $0$ 和 $n$ 。只要连续操作 1 就可以把序列任意循环移位，所以把序列当做环。

这里给出两个做法，一个是我的垃圾做法，一个似乎是来自 gmh77 的。

注意到 1 非常特殊，而其他数虽然跳的步长较长，但只要有别的数垫着，也可以"看做"很短。比如用 1 垫着 2 ，两个数就可以任意移动。

这可以引出一个高于指数级的做法，没啥用。

但是可以多个数一起走。假设当前已经做到了一个区间的数是 $k,k-1,\cdots,1$ ，考虑怎么往前走一步。先让 1 往前走，换回来一个 $x$ ，然后让 2 往前跳，把 1 换到后面去，再让 1 走回来，再跳 3 。这样在 ${1\over 2}k^2+O(k)$ 的次数内即可使得这一串数往前走一步。

那么就很显然可以用 $O(n^3)$ 的次数把所有数串成 $n-1,\cdots,1,0$ ，考虑怎样把它们翻转。发现就用上面走路的方法，只不过把顺序改成从大到小即可。最终操作次数是 $O(n^3)$ ，但带个至少 ${1\over 12}$ 的常数。

而 gmh77 的做法显然更加优美。

注意到一直操作同一个位置，在跳出 $0$ 之前得到的数互不相同。从小到大、从后往前，即可得到 $n-1,n-2,\cdots,0$ 的序列，然后再用同样的方法翻转即可。操作次数 $O(n^2)$ 。

AGC002F Leftmost Ball

以下某一些是补之前的题解。

考虑一个序列能否被构造出来。把每种颜色的第一个位置拿出来，用它们去和 0 匹配，需要使得每个 0 都能往后匹配一个位置。显然可以贪心，从前往后枚举 0 ，匹配后面第一个未被匹配的位置。这种匹配方式也是唯一的。

所以考虑所有这样的二元组 $(0,i)$ 在序列中的位置（区间），它们只需要满足互不包含。从后往前考虑每一个 $(0,i)$ ，要把剩下 $K-2$ 个同种颜色的球往后丢。由于后面的球都已经放好了，所以这种颜色的球往后放的方案数就是一个组合数。

设 $dp_{i,j}$ 表示考虑到了第 $i$ 个二元组，这个二元组的区间中还有 $j$ 个球，的方案数，前缀和优化转移。

一些看了但是不想写题解的题

可能是之前做过懒得回忆的，也可能是难度不太够的。放在这里表示看过题了。

click to open

AGC009F
AGC011E
AGC012E
AGC013E
AGC014E
AGC015DE
AGC016EF
AGC017DE
AGC018DF
AGC019DE
AGC020DE
AGC021D
AGC022EF
AGC023DEF
AGC024E
AGC025DE
AGC026DE
AGC027DF
AGC029DE
AGC030DEF
AGC031DE
AGC032DE
AGC033DE
AGC034DEF
AGC035DEF
AGC036DF
AGC037DEF
AGC038DEF

AGC011D Half Reflector

考虑一次操作会发生什么。如果左边第一个是 A ，那么变成 B ，无事发生；否则，第一个变成 A ，考虑第二个是 A 还是 B ，手玩一下会发现，球会跑到第二个和第三个之间，并且此时第二个也是 A ，第一个变成原来第二个的逆。

也就是说，一次操作要么把第一个从 A 变成 B ，要么循环移位并取反。容易发现做 $2n$ 次之后就有长度为 2 的循环节，那么模拟即可。

AGC011F Train Service Planning

题目的意思是列车时间表要有长度为 $K$ 的循环节。

容易发现，只要存在 $2A_i>K,B_i=1$ 就无解，否则有解。

把从 $n$ 到 1 的车时间逆转，变成从 1 开始，但是逆着时间运行。再调整一下，顺着时间的车卡在时间 0 不动，逆着时间的车要用 $2A_i$ 的时间才能通过。

如果枚举了逆车到达（或者出发？） 1 的时间，那么有一个很显然的贪心：每次能走就走，否则等到 0 （也就是 $K$ ）再走。

按照那个图从上到下 DP ，设 $dp_{i,t}$ 表示要在 $t$ 时刻到达 $i$ 所付出的最小代价，转移就是删除前缀并在最后加一个点，用一个 set 即可维护所有这样的点。但是初值还有一整个区间的 0 ，它们用线段树维护比较方便。

AGC012F Prefix Median

考虑怎样得到一个序列 $b$ 。有这样一个贪心：每个时刻，如果当前的 $b_i$ 还未出现就把它加入 $a$ 中，然后用还没有放进 $b$ 的最大最小值调整中位数。显然一次调整只能让中位数移动一格。

也就是说，集合 $A$ 长成这样：中间是一堆零散的作为中位数出现过的数，两边是连续的前缀后缀。

那么容易得到合法序列 $b$ 的必要条件：

每个位置都有上下界，分别是全部取最大和全部取最小所得到的中位数。
不存在 $j<i$ 满足 $\min(b_{i-1},b_i)<b_j<\max(b_{i-1},b_i)$ ，即不能一次移动两步。

可以用上面的构造来证明这是充分条件。

一种想法是直接用构造方法来 DP ，然而由于有相同的数存在，细节爆炸，不知道能不能做。

注意到条件中只关注相对大小关系，所以可以在确定上下界之后就不再考虑一个数出现多次，然后设 $dp_{i,j,k}$ 表示确定了前 $i$ 个位置，有 $j$ 个不同的数现在仍在合法区间中，当前的中位数是第 $k$ 个，的方案数。随便转移。

AGC013D Piling Up

这里给出两种做法，一种是我的垃圾做法，一种是官方题解做法。

先拿，再加，再拿，显然显得很蠢。可以把第一个拿和最后一个拿删掉（它们反正是任意的），然后操作就变成了每次加两个再拿两个。

如果拿的是 rb 或 br ，那么对盒子里的球没有影响；否则红球数会加一或减一。

我的垃圾做法：求出每个初始红球数量的合法解个数之和，减去相邻两个红球数量都合法的解个数之和。

把 rr 和 bb 分别看做向上或向右走两格， br 和 rb 看做向右上走一格，那么一个合法解就对应一条 $(0,0)$ 到 $(x,y),x+y=2m$ 的路径，要求路径不碰到直线 $y=x+i$ 和 $y=x+n-i+1$ 。

这个东西可以用「JLOI2015」骗我呢的容斥做法解决。

题解做法：

直接设 $dp_{i,j}$ 表示做完了前 $i$ 次，当前有 $j$ 个红球，的方案数，初始值全部设为 1 ，跑一遍 DP 即可得到「每个初始红球数量的合法解个数之和」。

对于「相邻两个红球数量都合法的解个数之和」，只需要把 DP 稍微修改一下即可。

（我真是个 sb ）

AGC013F Two Faced Cards

先考虑怎样判断一组数是否合法。把 $Y$ 离散化成 $[1,n]$ ，也把 $Z$ 对应搞成 $[1,n]$ 。对于 $Z$ 里面的 $z$ ，给 $[z,n]$ 加一； $Y$ 里面的 $y$ ，给 $[y,n]$ 减一。那么合法当且仅当得到的序列都非负。

先假装所有数都选择正面。如果变成反面，相当于给序列的一个区间加一。

对于一次询问，分别考虑它选正反面的情况，会给后缀加一。所以只需要考虑 $X,Y$ 使得某个后缀至少为 $-1$ ，其他位置至少为 0 ，的最大收益。

先把所有位置都搞成至少为 -1 ：考虑最右边的 $<-1$ 的位置，它至少会被覆盖一次，我们直接选择覆盖它的左端点最小的区间。

为什么呢？设 $c_i$ 表示位置 $i$ 至少需要再被覆盖几次，设 $p$ 是最右边的 $<-1$ 的位置， $q>p$ 。考虑最终选的区间中覆盖 $p$ 的右端点最小的区间 $J$ ，把它换成上面说的那个区间 $I$ ，会发生什么。如果 $J$ 没有覆盖到 $q$ ，或者 $c_q=0$ ，那么显然没有任何问题，否则 $q$ 会被少覆盖一次。但是注意到 $c_p>c_q\ge 1$ ，所以既然 $J$ 覆盖到了 $q$ ，就一定还有另一个线段覆盖到 $q$ 。此时把 $J$ 换成 $I$ 同样没有问题。

所以从右往左扫一遍，用优先队列维护当前存在的区间，即可使得所有数至少为 -1 。

-1 到 0 就很简单了，从左往右贪心，见到 -1 时用右端点最大的区间覆盖它即可。

AGC014F Strange Sorting

什么牛逼题目……

每次操作一定会把最大值丢到后面去，所以可以发现操作次数一定小于 $n$ 。但是这个操作过于神奇，显然不能逐步模拟。（可能出题人也这么认为，然后就被干掉了）

从大到小不好搞，所以反向考虑。注意到 1 在操作中起到的作用是很小的（不对其他元素造成影响），考虑求出删掉 1 之后的序列答案，然后推回当前序列的答案。

设删掉 1 之后的答案是 $T$ （记得特判 $T=0$ ），那么现在的答案只能是 $T$ 或者 $T+1$ ，要看 $T-1$ 次操作之后 1 是否在 2 前面。

可以发现 $T-1$ 次操作之后第一个元素不可能是 2 ，设这个元素是 $f$ 。那么有一个非常神奇的结论：

在前 $T-1$ 次操作中， $1,2,f$ 相对位置组成的环（有两种， $(1,2,f)$ 和 $(1,f,2)$ ）保持不变。

为了证明这个结论，还要先发现另外一个神奇的结论：

在前 $T-1$ 次操作中，不存在一次操作，使得 $f$ 不是第一个并且是 high 。

第二个结论可以反证，如果存在这么一次操作那么 $f$ 在这之后不可能是第一个元素。

有了第二个结论之后可以分类讨论证明第一个结论。

有了第一个结论之后只需要看初始的环是 $(f,1,2)$ 还是 $(f,2,1)$ 即可。

AGC015F Kenus the Ancient Greek

求 $\gcd$ 的算法可以被写成一个数列 $\{a_i\}_{i=0}^n$ ，满足 $a_0=0,a_{n-1}\le X,a_{n}\le Y,a_i=b_ia_{i-1}+a_{i-2}$ ，其中 $b_i\in \N^+$ 。

显然斐波那契数列是最优解之一。为了最大化长度，显然有 $a_1=1$ 。

观察样例发现对于 $i<n$ 似乎有 $b_{i}\le 2$ ，即中间的位置不可能在 $a_{i-1}+a_{i-2}$ 的基础上多加两个 $a_{i-1}$ 。设 $a_{i-1}=x,a_{i}=y$ ，那么有 $a_{i+1}=x+y,a_{i+2}=x+2y$ 。由于这是最优解，所以从 $(x+y,x+2y)$ 开始走的步数一定小于 $(y,x+y)$ 开始走的步数。而如果令 $a_{i}=2x+y,a_{i+1}=3x+y$ ，则有 $2x+y>x+y,3x+y\ge x+2y$ ，步数也严格小于 $(y,x+y)$ 的步数，不可能是最优解。

至此获得了一个 $O(2^n)$ 枚举 $\{b\}$ 的做法，但还不够优秀。

盲猜 $b_i=2$ 只能最多有一个位置，发现猜对了。证明可以考虑斐波那契数列的各种性质推一推式子，用类似上面的方法得到多于一个位置时一定不是最优解。注意以上这些 $b_i$ 不包括 $b_n$ ， $b_n$ 是可以很大的。

所以预处理出每种 $b_i$ 得到的数列，然后询问的时候求答案即可。

AGC016D XOR Replace

这题可能比后两题还稍微有意思一点？

容易发现异或是假的。设 $a_0=\oplus_{i=1}^n a_i$ ，那么一次操作就是交换 $a_0,a_i$ 。现在要用最少的交换次数把 $a$ 变成 $b$ 。

如果 $a$ 里面的元素互不相同，那么容易想到在 $a_i=b_j$ 时连边 $i\to j$ ，会连出若干个环。最后答案就和点数、自环个数、环个数有关。

换一种建图，连边 $a_i\to b_i$ ，那么新图中的一个环可以对应回原图的一个环。新图的每个弱连通块显然都有欧拉回路，所以一个弱连通块就是一个环，很容易计算答案。

AGC017F Zigzag

显然一条路径可以被写成长度为 $n-1$ 的 01 串，但是这个串的性质不是很好，所以还是写成点编号组成的序列。

直接设 $dp_{i,s}$ 表示第 $i$ 条链的路径是 $s$ 的方案数，转移就是无脑求高维前缀和，然后再根据限制把不合法的状态删掉。

复杂度 $O(nm2^n)$ ？错了，这里无脑求高维前缀和的复杂度是 $O(n^22^n)$ ，炸了。

考虑求高维前缀和的过程，其实也是一个 DP ： $dp_{i,j,s,t}$ 表示考虑到第 $i$ 位，新的链的前 $i$ 位是 $s$ ，旧的链第 $i$ 位在第 $j$ 个点，后面的状态是 $t$ ，的方案数。枚举第 $i$ 层 $j$ 变成 $i-1$ 或 $i$ 来转移。

但是注意到 $j<i-1$ 时是可以把它往右“掰”的。借用题解里的图(左)：

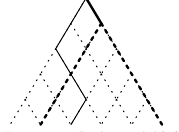
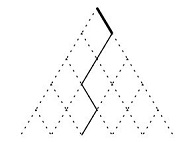
那么可以修改一下细实线，变成这个样子(右)。

于是把 $j$ 这一维干掉了，就做完了。

AGC018E Sightseeing Plan

两次做这题，两次被降智打击，不是很懂……

先随便推一推一个点到一个矩形的方案数，容易发现就是四个组合数加加减减。

我们要统计所有从第一个矩形到最后一个矩形的路径，与第二个矩形的交的长度之和。一个重要性质是，只要确定了进入和离开第二个矩形的点，那么方案数和长度就都确定了。

然后我就开始想奇奇怪怪的卷积……

事实上长度是两个点的坐标相减，可以直接把贡献拆开，然后就只需要枚举一个点了。我真是个sb。

AGC019F Yes or No

显然回答什么与这题的正确答案是什么没有任何关系，所以对于当前还剩下 $i,j$ 时我一定会有 ${\max(i,j)\over i+j}$ 的概率回答对。

那么可以考虑每一对 $(i,j)$ 的贡献，答案就是

\[{1\over {n+m\choose n}}\sum_{i=0}^n \sum_{j=0}^m [i+j\ne 0] {\max(i,j)\over i+j}{n+m-i-j\choose n-i}{i+j\choose i} \]

（这个式子应该是没问题的吧？）

然而这东西我好像只会分治 FFT ，于是裂开了。

考虑变成走路题，从 $(n,m)$ 开始，每次可以往下或往左走一步，每一种走到 $(0,0)$ 的方案都对应一种答案序列。考虑怎么计算一个答案序列的贡献。

不妨假设 $n\le m$ 。从直线 $y=x$ 切开，那么答对的题目就是在左上角梯形中往下走的步数，加上右下角三角形中往左走的步数。而往下走的总步数是确定的 $m$ ，所以可以转化为右下角三角形中往左走的减去往下走的步数，再加上 $m$ 。

但是这两个东西好像永远相等啊？？

漏统计了在直线 $y=x$ 上走的步数。所以现在只需要统计在 $y=x$ 上往左走的步数的期望，即经过 $y=x$ 的次数的期望除以 2 。

那就枚举每个点即可。

AGC020F Arcs on a Circle

好题，可惜看完题解之后就忘不掉了（

把长度最长的线段的左端点的坐标作为 0 ，即可断环为链。现在考虑两个线段能否相交，发现除了它们坐标的整数部分以外，就只和小数部分的大小关系有关了。所以可以 $O(n!)$ 枚举小数部分的大小关系，然后暴力从左到右状压 DP 即可。

忘记在哪里可以找到更好的做法了。

AGC021E Ball Eat Chameleons

又见到这题了。

考虑怎样判断一个序列是否合法。容易想到一个贪心策略：把第 $n$ 个变色龙单独拿出来；拿到红球时，如果前 $n-1$ 个还有没变色的那就直接吃，否则喂给第 $n$ 个；拿到蓝球时，如果前 $n-1$ 个有红色变色龙可以吃掉这个而不变色的那就吃掉，否则也喂给第 $n$ 个。

显然最终前 $n-1$ 个变色龙要么吃的红球比蓝球多一个（称这种情况为浪费），要么相等。设有 $A$ 个红球， $B$ 个蓝球，显然有 $A\ge B,A\ge n$ 。

我们只关心第 $n$ 个变色龙最终的颜色。显然，如果它吃的红球个数大于蓝球那么一定合法；否则在相等的时候最后吃的球必须是蓝球。

考虑浪费的球数 $m$ 。

如果 $A-m\ne B$ 那么直接比较大小关系。

否则，假设 $A\ne B,m\ne 0$ 。此时如果最后吃的球是蓝球，那么吃这个球的时候前 $n-1$ 个变色龙一定还有至少 $m$ 只没有吃过红球。这也说明此时第 $n$ 只变色龙也没有吃红球，所以最终第 $n$ 只变色龙只吃了一个蓝球。这显然是矛盾的，所以最后吃的球一定是红球，即一定不合法。

否则就只能是 $A=B,m=0$ 。这种情况稍微特殊一点，最后再讨论。

考虑怎么求出 $m$ 。容易想到把红球看做左括号，蓝球看做右括号，匹配出 $w$ 对，就有 $m=\max(n-1-w,0)$ 。而 $w$ 很容易计算，和最小前缀和什么的有关系。

所以当 $A\ne B$ 时，只需要 $A-B>\max(n-1-w,0)$ ，即 $A-B>n-1-w$ 。

而 $A=B$ 时需要满足什么条件呢？找到前 $n-1$ 对括号，剩下的都是喂给第 $n$ 个变色龙的。如果第 $K$ 个球是红球那么显然不合法，否则考虑它是否组成了第 $n-1$ 个括号。如果它不是第 $n-1$ 个括号的右括号，即喂给了第 $n$ 个变色龙，那么显然是合法的；否则喂给第 $n$ 个变色龙的球必须一个括号都组不出来，即 BBB...BRRR..R ，肯定不合法。

综上， $A>B$ 时只需要能组出 $n-(A-B)$ 个括号，而 $A=B$ 时需要最后一个球是蓝球，并且前 $K-1$ 个球能组出至少 $n-1$ 个括号。

这东西用翻折法随便搞搞即可。

AGC021F Trinity

关键在于选好 DP 顺序。

考虑给每行钦定一个最靠左的黑格子位置，然后每列就独立了。

从右往左 DP ，枚举这一列有几个位置是对应行的最左黑格子，然后这几行就相当于被删掉了。

每次转移的时候是一个卷积，用 NTT 优化到 $O(nm\log n)$ 即可。

AGC022D Shopping

首先注意到如果 $t_i\ge 2L$ 那么可以令 $ans\gets^+ 2L,t_i\gets^-2L$ 。

然后要想到一个方案的时间可以根据列车碰到 $0$ 和 $L$ 的次数来计算，而不需要考虑中间是怎么走的。

现在考虑从某个方向进入某个站，购物完成出来的时候会是怎样的。用两次来保证方向不变是一定可以的，但是如果 $t_i$ 够小就可以只用一次但方向改变。还有最右边的站比较特殊，它必须把向右的车变成向左的车，如果一次做不到那就三次。

如果是用两次来保证方向不变，那么这个站其实除了 $2L$ 的贡献以外没有别的变化，可以直接把它删掉（注意最右边的那个站是不能删的）。剩下的情况就变得有些奇妙。如果用一次碰到的是 $0$ ，那么把它看做左括号（额外把 $0$ 也看做左括号），否则看做右括号，那么左右括号必须能够匹配。按照左括号的位置从小到大做，也容易构造出一组合法解。括号的贡献是 1 ，其他的贡献是 2 ，所以我们要最大化匹配括号的个数。

每个站都有 $(0,0),(1,0),(0,1),(1,1)$ 四种状态，表示能否作为左右括号。先把 $(0,0)$ 删掉。从 $L/2$ 处切开，那么左边的站要么是 $(1,1)$ ，要么是 $(0,1)$ （ 0 除外），右边同理（第 $n$ 个站除外）。然后就随便做了。

AGC024D Isomorphism Freak

考虑一棵树的颜色种类数最少有多少种。找出它的直径，那么至少有 $len/2$ 个等价类。

显然这个下界是可以达到的，只需要以直径中点为根，使劲补叶子，使得每一层的点的度数都相同。

然而有各种特殊情况，所以最好把每一种有点可能的情况都冲一遍，反正 $n\le 100$ ，还没要求计数。

AGC024F Simple Subsequence Problem

先回忆一下判子序列的贪心算法。

由于贪心的时候只关心后面还剩什么东西，所以可以把给出的串反过来插入字典树中，然后每个点维护两条出边，分别表示加入一个 0 和加入一个 1 之后会转移到哪个点。

现在考虑一个串怎么求包含它的串的个数。一开始给每个给出的串在字典树上对应的位置放一个球，然后每加一个字符就让所有球走一步。

枚举串的过程也可以在字典树上枚举，即每次给原串加一个字符。但是球的个数太多，暴力走肯定是不行的。

注意到走了 $x$ 步之后球的深度就小于 $n-x$ ，即只有 $2^{n-x}$ 个有用的球的位置，所以可以维护每个位置的球的个数。长度小于等于 $x$ 的串的个数恰好是 $2^x$ ，于是两个乘起来刚好复杂度正确。总复杂度 $O(n2^n)$ 。

AGC025F Addition and Andition

考虑一次操作到底会发生什么。如果一位上有两个 1 ，那么相当于这两个 1 都往前走了一步；否则不变。

那么显然的一点是总 1 个数不会增加，并且会在进位的时候减小。所以进位暴力做是不会出事的。

既然移动和进位都是让 1 往高位走，那不妨从高往低做，确定高位目前的状态时候再让低位的 1 往前走。显然这样是很对的。

找到当前的一对 1 ，让它往前走。显然在撞上另外一个不动的 1 之前，它只会一步一步挪，所以可以快进到撞上 1 ，然后无脑进位即可。

没了？没了。如果用栈维护后面第一个 1 可以做到线性，但是我选择直接用 set 1700ms 擦过。

AGC050F NAND Tree

乱入

这个 mod 2 显然非常特殊，要尽可能地把所有方案两两放到一起使得它们抵消。

考虑最后两步，还剩三个点的时候，设点权分别为 $x,y,z$ 。如果 $x=z$ 那么合并 $(x,y),(y,z)$ 的顺序对结果没有影响，所以贡献为 0 。而容易发现 $x\ne z$ 时得到 0/1 的方案数恰好都是 1 。

所以可以枚举最后两条边。由于中间一块的结果对最终结果没有影响，所以它的大小不能超过 2 ，否则 $(n-1)!=0\pmod 2$ 。然后求两边得到 0/1 的方案数。

注意到只要一棵树的大小超过 2 ，那么它合并成 0 和 1 的方案数（的奇偶性）是相等的。所以两边必须有至少一边的大小是 1 或 2 ，不然乘在一起的答案相同，加起来也变成 0 了。

较小的和中间的点数不能同时是 2 ，否则合并的时候乘的组合数会变成 0 ；如果有一边是 2 那么 $n$ 必须是偶数，否则组合数也会是 0 。

所以 $n$ 是奇数时就只需要计算每次删两个直到 $n=3$ 且两个叶子的数值不相等的方案数。

$n$ 是偶数的情况更恶心一点。但是注意到一次删三个的方案总是两两一组，所以另外一块的大小只能是 1 （否则 01 的方案数又相等了，拼在一起又消失了），即只有最后一步还剩 4 个点的时候有操作空间。枚举最后 4 个点即可。

复杂度写得比较垃圾是 $O(n^4)$ 的，但是加了一点剪枝，可能出题人也懒得卡，就跑得飞快。

AGC051C Flipper

一题做了 3h ，不愧是我。

由于操作都是异或什么的，判断初始状态能否到达某一个终止状态只需要判断能否把它们两个的异或消成全 0 。

一个简单的想法是贪心把它消成只有左边两列和最后一行有值，并且观察到

每列的 1 的个数的奇偶性确定；
每行的 1 的位置按照模 3 余数分类之后的奇偶性只能是原来的或是每一位都异或 1 。

于是可以发现消成这个状态的方法是唯一的。

所以就只需要判断 1. 每一列都有偶数个 1 ； 2. 每一行的状态只有 $(0,0,0),(1,1,1)$ 两种，且后者的个数是偶数。

那么对应回最终的矩阵，就要求 1. 每列的奇偶性相同； 2. 每行 &#&￥@#￥￥*

然后乱搞就各凭本事吧。我搞了一小时真是菜死了……

AGC051D C4

怎么 Atcoder 也考论文题，幸好我昨天刚看过（

我们会对有向欧拉图的欧拉回路计数，但是这里有两个问题，图是无向的，且起点终点相同的边是不可区分的。第一个问题很好解决，因为可以发现只有 $O(a)$ 种定向的方法。

对于第二个问题，可以考虑魔改欧拉回路计数问题的解法。原解法是任取一棵内向树，然后任意排列其他的边。这里还是任取一棵生成树，但把排列变成组合即可。

也有 FFT 做法。我一开始想的是每回到 $S$ 一次就算一个回路，然后得到了一个 $O(n^3)$ 的式子完全不会优化……正解是把 $S,U$ 之间反复横跳作为一个小段，然后不知道怎么操作一下就得到了一个 FFT 。

AGC051E Middle Point

设读入的点是 $P$ 。一个点 $Q$ 能被搞出来，当且仅当 $\sum w_iP_i=Q$ ，其中 $w_i$ 非负，其分母是 2 的幂，且 $\sum w_i=1$ 。

如果把分母是 2 的幂这个条件都忽略掉，那么就可以组出凸包内的所有整点。然而这显然是不能忽略的。

直接给出结论：

如果 $Q$ 在凸包外，那么无法得到。
如果 $Q$ 在凸包边界上，那么只能用边上的这两个点得到。
如果 $Q$ 严格在凸包内部，那么可以忽略“非负”这个条件。

前两点非常显然，第三点非常迷惑。

可以发现现在要找的就是一组非负整数 $c_i$ ，使得 $\sum c_iP_i=0$ ，且 $\sum c_i$ 是 2 的幂次。

考虑如果找到了一组整数 $d_i$ 使得满足上面两个条件，那么可以再找一组正整数 $e_i$ 使得 $\sum e_iP_i=0$ （这个可以先找到一组正有理数解，然后乘上分母的 $\text{lcm}$ 的若干倍）。现在令 $t=\left\lfloor2^k/\sum e_i\right\rfloor$ ，其中 $k$ 足够大，然后令 $s\sum d_i+t\sum e_i$ 是 2 的幂，然后 $c_i=sd_i+te_i$ 就满足条件了。

那么忽略“非负”之后怎么做呢？先强制 $w_i$ 是整数，然后考虑 $\sum w_iP_i$ 在 $\sum w_i=1$ 时能凑出哪些点。可以令 $P_1$ 是原点，把 $\sum w_i=1$ 的限制去掉。此时就是一堆向量的线性组合，用辗转相除可以得到两个向量 $A,B$ ，得到点的集合就是 $\{nA+mB\mid n,m\in \Z\}$ 。

然后以 $A,B$ 为基，对坐标系进行一些操作，使得一个点能被表示出来当且仅当它是整点。

回想起来 $w_i$ 还可以是分母为 2 的幂的有理数，所以在新坐标系中还要加上两维的分母都是 2 的幂的点。可以发现这样对辗转相除法的正确性没有影响。

但是对应回原坐标系也要是整点，所以考虑新坐标系中哪些点满足这个条件。

设基向量分别是 $A=(a,b),B=(c,0)$ ，且 $a=2^\alpha A,b=2^{\beta }B,c=2^{\theta}C$ （请忽略变量重名和奇怪字母用法等等）。设新坐标系中的点 $(x,y)$ 对应回去是 $yA+xB$ 。那么有限制

$by$ 是整数，即 $2^{-\beta}|y$ 。
$ay+cx$ 是整数。

第一个好处理，但是第二个怎么办呢？注意到如果 $\alpha\ge \beta$ 那么可以忽略掉 $ay$ ，而如果 $\theta \le \alpha$ 那么可以让 $A$ 加上若干个 $B$ 之后得到 $\alpha'>\beta$ ，所以唯一的问题就出在 $\alpha<\min(\beta,\theta)$ 。

脑洞一下，这时候可以交换横纵坐标，让 $A,B$ 重新做一遍辗转相除得到 $A',B'$ ，可以发现此时就一定有 $\alpha\ge \min(\beta,\theta)$ 了。

然后就可以把 $ay$ 忽略掉，得到限制 $2^{-\theta}|x$ 。现在横纵坐标独立，所以可以分别拉长 $2^{\beta},2^{\theta}$ 倍，求凸包内整点数即可。

辗转相除的时候值域可能很大，开 __int128 。提交记录

AGC026F Manju Game

首先，先手肯定有一个策略是拿边上的球，然后结果就固定了。称这个策略为基本策略。然后按照盒子个数的奇偶性分类讨论。

奇数

如果先手拿了偶数位置的球，那么不管后手往哪边走，子问题中先手还是先手；否则后手可以使得先手变成后手。注意到先手一定不会使得后面那种情况发生，因为在这种情况下后手可以强制先手只获得基本策略的收益。

所以先手一定会先拿几次偶数位置的球，最后在某个区间中采取基本策略结束游戏。可以设先手的基础收益是所有偶数位置的球，那么最后还要加上区间中奇数位置减偶数位置的球。所以可以二分额外收益，然后以确定能走到有额外收益的区间为胜利。

那么先手的策略可以被写成一棵类似线段树结构的二叉树，每次从一个偶数位置劈开，两边的区间都是必胜态。能造出这么一棵树当且仅当存在一组必胜区间能恰好覆盖所有奇数位置，这个可以随便 DP 。

偶数

现在先手的基本策略的收益是 $\max(odd,even)$ 。由于先手不管走哪里，在子问题中都会被后手强制变为后手，所以最优解就是直接取基本策略。

AGC028D Chords

注意到 $n\le 300$ 长得有点像区间 DP 。

考虑一个连通块长什么样。它会连接零散的点，把整个圆切成几个部分，每个部分只能内部连边。

考虑怎么把一个连通块和某个东西对应起来。经过一通乱撞之后想到，可以把它对应到 1 和 $n$ 中间的空位所在的部分，即记录连通块中点编号的 $l=\min,r=\max$ 。

然后怎么转移呢？考虑先随便连边，那么可能 $(r',r]$ 没有和 $l$ 连通，需要减掉。为了不减多，还需要令 $l,r'$ 连通。显然这就转移到子问题了。

AGC028E High Elements

显然原来的前缀最大值（ $A$ 类点）也会是现在的前缀最大值，而其他值（ $B$ 类点）都可以选择把它忽略。所以在单纯想判断合法的情况下只需要一边有 $B$ 类点的贡献。

考虑如何判断能否分配一个序列，使得两边的差为 $d$ （而不是 0 ）。同样只需要有一边有 $B$ 类点的贡献，所以假设这一边减去另一边得到 $d$ 。如果把这边的一个 $A$ 类点移动到另一边，那么 $d$ 会减 2 ；如果移动 $B$ 类点则 $d$ 会减 1 。

所以我们可以在确定奇偶性的情况下尽可能最大化这个差值，然后与 $d$ 做比较，只要能凑够 $d$ 且奇偶性对，并且 $d$ 不是太小（差值不会小于剩余的 $A$ 类点的个数）。具体来说，我们要找到一个最长的带权 LIS ，其中 $A$ 类点的权值为 2 ， $B$ 类点的权值为 1 ，并且长度的奇偶性与 $d$ 相同。这显然可以数据结构优化 DP 。

回到原题，只需要贪心从前往后分配，然后用上面的方法维护每一个后缀的信息即可。

AGC028F Reachable Cells

参考 https://www.cnblogs.com/turboboost/p/Reachable-Cells.html 。好像找不到中文的官方题解做法，所以自闭了。正解似乎是 $O(n^2\log n)$ 的。

考虑对图进行一些操作。做完 $(x,y)$ 的答案之后，如果它上面和左边都是墙，那么它就不会再对其它格子造成影响了，可以也置为墙，把它置为墙之后还可以递归改别的格子。

现在一个格子能到达哪些格子呢？可以用两条边界把它们框起来，使得框的范围中的空地全都可以被到达。边界分为上边界和下边界，都是往右往下延伸的一条线。

证明：

由于边界最小，容易发现下边界的往下走的部分都是可达的，上边界的往右走的部分都是可达的。

考虑被框起来的一个格子，它总是可以往上或往右走，所以一定可以走到边界上，所以可达。

这就是一个很强的性质了。一个显然的推论是能到达的格子在每一行组成了一个区间，所以直接把右边的格子和下面的格子的区间合并起来就可以得到自己的区间。

每次做完一行之后把能删的删掉，然后重新处理每一行的前缀和。复杂度 $O(n^3)$ 。

AGC029F Construction of a tree

大胆猜想某一些条件合在一起就是充要条件。经过颅内随机游走，可以想到：任取一个点集 $S\,(|S|\ne 0)$ ，完全包含在 $S$ 内的集合个数不能超过 $|S|-1$ ，且这是充分条件。

证明：

设 $f(S)$ 表示包含在 $S$ 内的集合个数。

如果这个条件满足，那么任取 $f(S)=|S|-1,f(T)=|T|-1,S\cap T\ne \varnothing$ ，会有 $f(S\cap T)=|S\cap T|-1$ 。

现在找到最小的 $f(S)=|S|-1,|S|\ne 1$ ，在里面任意用一个集合 $E$ 连接一条边 $(u,v)$ 。如果用掉之后不合法，那原来一定存在一个 $u,v\in T,f(T)=|T|-1,E\nsubseteq T$ ，所以 $f(S\cap T)=|S\cap T|-1$ ，与 $S$ 最小矛盾。

重复这个过程直到只剩一个点即可。

这个条件等价于任取 $k\,(k\ne 0)$ 个 $E$ ，它们的并集的大小要超过 $k$ 。也就等价于任意删掉一个点后 $V$ 和 $E$ 存在完美匹配。

从 $E$ 往 $V$ 跑一个匹配，会剩下一个孤立点。从这个孤立点开始跑一个增广路树，如果能遍历到整个 $V$ 那么就容易构造出解，否则任意删掉一个不能被遍历到的点之后就没有完美匹配了。

AGC031F Walk on Graph

先把过程反过来，变成从 $T$ 到 $S$ ，维护一个 $sum$ ，每走一步就 $sum:=2sum+w$ ，需要走到 $S$ 时 $sum=R$ 。所以状态数变成 $O(nM)$ 了。

考虑最小的 $t\,(t>0)$ 使得 $2^t=1\pmod {M}$ 。如果 $t$ 是奇数，那么在一条边上来回走 $t$ 次就可以在不改变 $sum$ 的情况下移动，所以本质不同的状态数只有 $M$ 种，可以暴力。

否则，走 $t$ 步会走回自己。考虑一个点旁边的两条边 $u,v$ ，先在 $u$ 上走 $2$ 步，再在 $v$ 上走 $t-2$ 步，就可以收获 $sum:=sum+3(u-v)$ 。

考虑从 $(x,sum)$ 走到 $(y,2sum+w)$ ，然后走 $t$ 的倍数步回到 $(y,2sum+w+?)$ ，然后再反复横跳，就可以走到 $(x,sum+{1\over 2}?)$ 。所以 $y$ 能得到的额外贡献 $x$ 也都可以得到。

综合上面两行，可以发现，可以把所有共顶点的 $3(u-v)$ 取 $\gcd$ ，并与 $M$ 取 $\gcd$ 得到 $m$ ，那么就只需要考虑模 $m$ 的结果了。

现在，每条边的权值都可以被写成 $w+k\cdot {m\over 3}$ 的形式，所以 $sum$ 一定可以被写成 $(2^a-1)w+b\cdot {m\over 3}$ 。注意到沿着一条边横跳两次，会变成 $(2^{a+2}-1)w+b\cdot {m\over 3}$ ，且 $2^t=1$ ，所以 $a$ 只需要关心奇偶性，所以点数被优化到了 $6n$ 个。又因为横跳 $t$ 次会走回自己，所以边是双向边。

综上，可以建出 $6n$ 个点的无向图，询问等价于判连通性。

AGC032F One Third

先是一个比较脑洞的模型转化：切完第一刀之后，以它为其中一刀，把蛋糕三等分，分别染上三种颜色。接下来的每一刀都会有一个颜色，而第一刀可以被认为有两种颜色。

然后画画图就可以发现/验证，最终选取的左右端点一定是不同颜色的两刀。如果给每一刀赋一个权值，为它到它的颜色的左边界的距离，那么选取的不同颜色的两刀带来的 $|{1\over 3}-x|$ 就恰好是它们的权值之差的绝对值。（同样的，第一刀的两个颜色对应两个权值。）

所以就可以转化成在长度为 ${1\over 3}$ 的线段上撒点，并且每个点可以任意分配颜色，要找到不同颜色的距离最近的两点。在 $0$ 和 ${1\over 3}$ 初始就有不同色的两点。

考虑把概率积分起来得到期望。如何求出答案 $>x$ 的概率呢？把中间的 $n-1$ 个点分配好颜色之后，假设有 $k$ 个相邻颜色不同的点，那么概率就是 $({1\over 3}-kx)^{n-1}$ 。积分得到 ${{1\over nk3^n}}$ 。

至于数 $k$ 个相邻颜色不同的点的方案数就是简单计数题了。

AGC033F Adding Edges

先考虑如果强制顺序就是 $a,b,c$ 怎么做。~~脑瘫晚期患者表示不会~~

可以直接枚举每一个点，以它为根在树上 dfs ，看往下走能走到哪些点。复杂度 $O(n(n+m))$ 。

但是顺序是可以任意的，这就比较恶心。考虑对给出的图进行一些操作，如果 $e_1-e_2=e_3$ ，那么就把 $e_1$ 删掉换成 $e_3$ 。

怎样快速完成这些操作呢？

这也是一个（我觉得）不太好想的做法：记录 $T_{u,v}$ 表示以 $u$ 为根，如果想要加入边 $(u,v)$ ，那么会被缩短到 $(T_{u,v},v)$ （即最长的从 $u$ 指向 $v$ 的边是 $(u,T_{u,v})$ ）。

加入一条边时，先用 $T$ 把自己缩到最短，然后以一个端点 $x$ 为根往另一个端点 $y$ 的子树 dfs ，假设 dfs 到 $z$ 。如果 $T_{x,z}=-1$ 那么显然只能把它标为 $u$ ，否则就是有一条边 $(x,z)$ ，那么把这条边缩短（放到队列里等待下次加入），并立刻返回。子树内的 $T$ 并不需要修改，因为能达到的最长的边没有变化。

一个小问题是，我们怎么知道会有这么一条边 $(x,z)$ 呢？这是因为每条边都会覆盖一整个子树，而我们在 $z$ 这里第一次遇到标记，所以必然有这条边。是否有可能它已经被缩短成 $(x,z')$ 或 $(x',z)$ 了呢？被缩短了但还没来得及加入？这个我不是很懂。这种在修改上面叠修改的题目好像一直不是很懂。

但是，如果假装没有这些奇怪的情况，那么 dfs 的时候遇到一个点要么缩短一条边，要么多打一个标记，所以复杂度 $O(n(n+m))$ 。

完成这些操作之后，就可以像一开始那样做了。

AGC036E ABC String

上次看这题的时候学长写了，而他已经 AFO 了……

首先肯定可以把相邻相同字符缩成一个。现在假设 C 的个数最少，那么一个简单的想法是猜想答案就是 C 的个数，然而这个上界是取不到的。

假设确定了若干个选取的 C 的位置，并把连续的删掉了。在选取足够的 A 时，不能让 B 太多。如果有 $b$ 个间隙必须放 B ，剩下 $u$ 个有 A 的位置，就要有 $b\le u$ 。对于 $a,v$ 同理。

猜想这是充分的，而后面的构造也证实了这一点。

显然 $b>u$ 和 $a>v$ 只有最多一个满足，所以不妨假设是 $a>v$ 。先把所有 C 都选上，然后有一些间隙只有一个 A ，那么可以把旁边的一个 C 删掉来消除这个间隙。一直删直到 $a\le v$ 。显然现在取到了 C 的最大值，并且 C 仍然是最少的。

现在来构造方案。

从左往右枚举每一段尝试删，使劲删，直到这一段的长度不超过 2 或是尝试删的这个字符的数量已经等于 C 。显然这么做之后仍然满足上面那个条件。

如果现在所有段的长度都不超过 2 那就可以随便删了。否则假设现在 B=C ，那么由于 $a\le v,b\le u$ ，所以把能删掉的 A 删掉一些之后一定也可以达到 A=C 。

ARC112F Die Siedler

显然（或者无脑猜想），操作顺序不会影响结果。

令 $N=n!2^n-1$ ，那么可以发现把一组牌 $A$ 重复 $N+1$ 次之后消出来的结果和原来的这组牌相同。

于是考虑重复 $N$ 次会消出什么。它满足 $A+B=A$ ，但又不能全部为 0 ，可以发现只能是 $\{1,3,5,\cdots,2n-1\}$ 。也可以发现任何一组牌加上它都不变，所以可以假装它是零。

而又注意到 $\{k\times A\}$ 的循环节中不会出现两个一样的牌组，所以好像有很好的性质。但最短循环节长度不一定就是 $N$ 。

找一个单位元。显然 $\{1,0,\cdots,0\}$ 就满足条件。现在可以把牌组对应到一个数了。如果它是 $\{a_i\}$ ，那么就令 $A=\sum_i (i-1)!2^{i-1}a_i$ ，然后加法就在模 $N$ 意义下进行。

然后用裴蜀定理，把给出的牌组与 $N$ 求 $\gcd$ ，那么模 $\gcd$ 与初始牌组相同的都可以得到。注意到 $\gcd$ 要么特别大要么特别小，然后乱搞即可。

AGC052C Nondivisible Prefix Sums

丢人……

考虑一个垃圾构造方法：从前往后放，每次随便放一个能放的。这种方法可能会在最后只剩下一种数的时候死掉。

设总和为 $sum$ ，对于一个数 $x$ ，设 $k_x=({sum\over x}\bmod P)-1$ ，那么最后就不能剩下超过 $k_x$ 个 $x$ 。

把每个 $x$ 超出 $k_x$ 的部分拿出来，那么我们需要及时把它们消掉。设超出的部分为 $c_x$ 。注意到我们每次可以做（最大值减一）和（最大值和次大值一起减一）中的一种，并且至少一个 $k_x$ 不为 0 （除非只有一种数），所以只要能把最大值消掉，就差不多可以把整体消掉。

为什么是差不多呢？因为可能现在恰好只超出了 $c$ 个最大值和 $c-1$ 个次大值，并且相加等于 0 ，并且次大值的 $k$ 是 0 ，并且没有其他的数，并且这一步只能放次大值。比如一共有 $P$ 个 1 和 $1$ 个 $-1$ ，且以前的前缀和是 $-1$ 。

但是只需要让 $k_x=0$ 的 $x$ 成为最大值就好了？

总之，只要能把 $c$ 的最大值消掉就赢了。转而考虑消不掉的情况。

不妨假设消不掉的是 1 ，那么对于其他的 $x$ ，一个 $x$ 就可以干掉 $P-x$ 个 1 。初始还可以白给 $P-1$ 个 1 。要求最后还能剩下 1 ，且总和不是 $P$ 的倍数。

前缀和优化背包即可。~~大概全世界就只有我不会背包了~~

AGC052D Equal LIS

LIS 是偶数的情况下，直接从左往右贪心，如果塞给第一组之后那组的 LIS 不超过 $len/2$ 那么直接塞，否则塞给另外一组。显然贪心结束之后两组的 LIS 都至少为 $len/2$ ，并且如果第二组的 LIS 超过 $len/2$ ，那么考虑它最小的那个元素，以它为中心可以扩展出一条 $len+1$ 的 LIS ，矛盾。所以 LIS 是偶数时一定有解。

LIS 是奇数的情况下如果仍然这么贪心，就有可能会使得第二组的 LIS 长度不够长。我们可以直接把较大的 $(len+1)/2$ 个 LIS 元素钦定给第二组，然后跑贪心，如果第一组够长那么就合法（证明和偶数情况类似）。然后再把较小的钦定给第一组，倒过来跑一遍。

如果两种都不行呢？把拿出来的这个 LIS 在中间切开，用第 $(len-1)/2$ 和 $(len+1)/2+1$ 个元素把坐标系分成九宫格，从左到右从上到下标号为 1~9 。那么显然可以发现，在第 2,3,4,5,6,7,8 块中只有拿出来的 LIS 的元素存在。如果存在解，那么一定有一组的 LIS 是 $7\to 9\to 3$ 或 $7\to 1\to 3$ ，不妨假设是前者。那么中间会剩下来至少 $(len+1)/2$ 个元素，可以组成另一组的 LIS 。经过调整可以使得两组的 LIS 都恰好是 $(len+1)/2$ 。

综上，只需要判三种（五种？）情况即可。

AGC052E 3 Letters

解题的关键在于找到好看的描述一个串的方法。

先把 ABC 转成 012 ，然后用一个折线来描述，满足 $|f(i)-f(i+1)|=1,f(i)=s_i\pmod 3$ 。那么能改变一个位置当且仅当 $f(i-1)=f(i+1)$ ，然后如果 $f(i)=f(i-1)+1$ 就减二，否则加二。

把 $s$ 和 $t$ 的折线放在同一个坐标系内，那么能改变的就只有 $f(1)-g(1)$ 的值。容易发现当 $f(i)=g(i)\pmod 2$ 时最小代价为 ${1\over 2}\sum|f(i)-g(i)|$ ，否则无解。

调整 $f(1),g(1)$ 的相对位置使得最小化代价即可。

AGC049F Happy Sequence

找了半天合法 $A$ 的性质然后发现没啥性质……唯一一个关于合法 $A$ 的性质是： $\sum A_i=\sum B_i=S$ 。所以移动的总次数确定。

把移动 $A$ 的代价差分，设 $D_{i,x}=C_i(1+2(x-A_i))$ 表示把 $A_i$ 从 $x$ 移到 $x+1$ 的代价，那么显然 $D_i$ 单调递增。

对于每个 $x$ ，设 $k_x=\sum_{A_i\ge x} (A_i-x)$ ，则 $k_x+nx-(S-k_x)\le \sum |B_i-x|$ ，即 $k_x\le {1\over 2}(S-nx+\sum |B_i-x|)$ 。显然 $k_x$ 单调不增。设 $lim_x={1\over 2}(S-nx+\sum |B_i-x|)$ 。

把 $D_{i,x}$ 视为放在 $i$ 处的物品，那么对于每个 $x$ ，这里的限制就是后缀不能拿超过 $k_x$ 个物品。并且最终需要恰好拿 $S$ 个物品，最小化总代价。

注意到 $D_i$ 从左往右代价单调增，而受益单调减，所以可以忽略先拿 $D_{i,x}$ 才能拿 $D_{i,x+1}$ 的限制，变成随便拿。

贪心即可做到 $O(n^2\log n)$ ：从后往前做，维护集合 $S$ ，每次把这个位置的物品全部加进去，然后把超出 $lim_x$ 的最贵的物品删掉。

由于物品太多，直接维护 $S$ 是不现实的。但是注意到代价仅仅是 $O(KL)$ ($K=\max C$) ，所以可以维护 $sz,mx,cnt_i$ ，表示 $S$ 的大小， $S$ 中的最大值和代价为 $i$ 的物品被删掉了多少个。（对于 $i>mx$ ，这种物品全部删完了。）

从 $x+1$ 移动到 $x$ 时，需要多来 $lim_x-lim_{x+1}$ 个物品。把 $x$ 处 $\le mx$ 的物品全部加进去，然后一步一步调整 $mx$ 直到 $S$ 中恰好 $lim_x$ 个。现在的问题是复杂度如何分析，即 $mx$ 会跳动多少次。设 $mx_x$ 表示做完 $x$ 之后 $mx$ 的值。

首先，由于 $lim$ 的定义，可以推出 $lim_x-lim_{x+1}=\sum [B_i>x]=dt_x$ ，所以 $n\ge dt_x\ge dt_{x+1}$。设 $F_x$ 表示放在 $x$ 位置的第 $dt_x$ 小的代价，那么 $mx$ 就可能需要从原来的地方移动到 $F_x$ 。注意 $D_{i,x}=D_{i,x+1}-C_i$ ，所以有 $F_x\ge F_{x+1}-K$ 。 $F_x$ 从右到左总共的减小量不超过 $O(KL)$ ，所以上升量也就是 $O(KL)$ 。

如果 $mx_{x+1}<F_x$ ，那么 $mx_x=F_x$ ，否则 $mx_x\ge F_x$ 。所以 $mx$ 的上升量是 $O(KL)$ ，所以总变化量 $O(KL)$ 。

变化一次的复杂度是 $O(K)$ ，所以总复杂度 $O(n+K^2L)$ 。

AGC048F 01 Record

先把串翻转，使得所有 01 交替串都以 1 为开头。称这样的串为好串，则较短的好串一定是较长的好串的前缀。

这是一个比较强的性质，可以推出一些结论：

要取出 $k$ 个好串使得 1/0 的个数最大时，最优做法就是每次取出最长的好串，因为能接在原来的串上时就没有必要新开一个串。
如果一个串能被拆成长为 $a,b$ 的好串，那么就可以被拆成长为 $c,d$ 的好串，其中 $a\le c\le d\le b$ 。
（没啥用）看一个串能否被拆成 $s_1,s_2,\cdots,s_m$ 时，最优做法是把第一个字符分给能接受它的最长的串。

根据 (1) ，可以每次取出最长的好串之后（得到 $l_1\ge \cdots\ge l_m$），发现一个合法的拆分方案必须满足前 $i$ 个串中的 0/1 的个数不超过 $l_1,\cdots,l_i$ 加起来的个数。根据 (2) ，似乎可以把两个过于分化的串中和一下。所以猜想这是充要条件。

猜中了。 DP 很显然。

如何从 $l$ 转化成满足条件的一组串？大概就乱搞吧。

AGC046F Forbidden Tournament

整点不一样的做法 /cy

度数的限制不是太大问题，考虑怎么处理第三个限制。

显然每次把入度为 0 的点删掉之后剩下的图必然强连通。不妨枚举入度为 0 的点有几个，然后只需要处理强连通图的情况。

那个子图不存在，等价于对于每个点 $x$ ，连向它的点的导出子图都形成了“一条链”（即没有环）。

维护一个序列 $b$ ，初始只有一个元素 1 。从左往右扫，扫到 $b_i=x$ 的时候，对于所有 $j>i$ 都有 $b_j\to x$ 这条边。把所有还未加入序列的连向 $x$ 的点全部加入，按照拓扑序与 $b_{i+1},\cdots,b_m$ 归并起来。最终得到 $b_1,\cdots,b_n$ 。为了方便，不妨假设 $b_i=i$ ，最后乘上 $(n-1)!$ 。

设 $a_i$ 表示扫到哪里的时候把 $i$ 加入了序列。特别地， $a_1=1$ 。显然满足 $a_i<i$ ，并且根据 $a$ 就可以还原出点之间的边的顺序：对于 $i<j$ ，如果 $a_j\le i$ 则 $j\to i$ ，否则 $i\to j$ 。另外因为图强连通，所以还需要 $a_n\ne 1$ 。

现在考虑怎样让连向 $i$ 的点满足条件。它们是 $1,2,\cdots,a_i-1$ 和 $j>i,a_j\le i$ 的点 $j$ 。这两段分别需要能排序，所以设 $mx=\max a_i$ ，则 $a_1=\cdots=a_{mx-1}=1$ 。然后这两段还需要能被合并在一起。但是根据两个点连边的条件，发现只能是前面全部连向后面，或是后面全部连向前面。所以有两种可能： 1. $\forall a_j\le i<j,a_j=1$ ；2. $\forall a_j<i<j,a_j\ge a_i$ 。

但是我们知道 $a_n\ne 1$ ，所以 $\forall a_n\le i<n,a_n\ge a_i$ 。而 $mx\ge a_n$ ，所以前面的 $a$ 都是 1 ，所以知道 $mx=a_n,(\forall i<a_n,a_i=1),(\forall i\ge a_n,a_i\le a_n)$ 。再考虑 $mx\le i<n$ 的 $i$ ，最终可以推出 $a$ 在 $[a_n,n]$ 上单调不降。

此时所有的限制都被满足，已经可以推出 $K=n-1$ 的答案了。

然后考虑入度。一个点 $i$ 的入度是 $a_i-1+\sum_{j>i} [a_j\le i]$ 。分类讨论 $i<mx$ 和 $i\ge mx$ ，可以推出

\[i-K\le a_i\le i+K+1-n\ (i\ge mx)\\ a_i=1\ (i<mx) \\a_i\le mx\\ n-K\le mx\le K+1 \]

（不知道有没有冗余条件，不管了）

然后数合法的 $a$ 的个数即可。

AGC040C Neither AB nor BA

先想一些贪心策略，然后发现好像怎么搞都和奇偶性有关。

这时就可以想到每次删除的时候必然一个来自奇数位一个来自偶数位（因为下标的奇偶性不变），所以可以把奇数位置的 AB 反转。

然后只要两者都不超过一半即可。

AGC040E Prefix Suffix Addition

又被自己菜死了……

考虑只有一种操作的时候会发生什么。比如只有操作 1 ，那么显然可以发现答案就是 $\sum_{i=1}^{n-1} [a_i>a_{i+1}]$ 。

把 $a_i$ 拆成 $b_i+c_i$ ，分别表示操作 1 的贡献和操作 2 的贡献。

但是此时发现好像没有什么贪心策略是有效的，所以只能考虑 DP ：设 $dp_{i,j}$ 表示做了前 $i$ 个， $b_i=j$ ，最小代价。

然后怎么办？

显然 $dp_i$ 单调不升。这时候的一个关键观察就是， $dp_{i,a_i}$ 和 $dp_{i,0}$ 只改变了这个位置的值，所以不会相差超过 2 。

也就是说 $dp_i$ 的值只有三种，那就随便做了。

AGC040F Two Pieces

双被自己菜死了……

想象有初始为空的两行。把操作 1 看做给某一行加一个球，把操作二看做加一根棍子把之后的操作和之前的操作割隔开。

因为题目的判重条件，可以认为每一段中第一行的球数都大于等于第二行的球数。那么第一行会有 $B$ 个球，第二行不确定。但是最后一段中第二行会比第一行少 $B-A$ 个球，而我们并不关心前面的段中球数具体怎么分布，因为不管怎么分布，最后一根棍子都会消除所有的差异。

然后转换到坐标系上，用 $(x,y)$ 表示两个 pieces 的坐标分别是 $x,y$ 。那么操作有三种：

$x:=x+1$ ；
$y:=y+1$ ，只能在 $y<x-1$ 的时候使用；
$y:=x$ 。

操作一用了 $B$ 次，不妨枚举操作二用了 $k$ 次。特判掉 $k+B=n$ 的情况。

假装我们确定了操作一和操作二之间的顺序，现在要加入 $n-k-B$ 个操作三进去。

“只能在 $y<x-1$ 的时候使用”，相当于除了刚进行完操作三的时候和刚开始的时候，不能碰到 $y=x$ 这条直线。

根据前面所说，最后一次操作三需要保证 $x-y=A-k$ 。而因为以后不会再碰到 $y=x$ 这条直线，所以在只考虑操作一二的时候，只有最后一次碰到 $x-y=A-k$ 时才能使用这最后一次操作三。

同理，只有在最后一次碰到 $x-y=A-k-1,A-k-2,\cdots,0$ 的时候才能使用操作三。并且这些位置是肯定会被碰到过的。而且每次使用的次数是任意的。

那么就把操作三的插入和操作一二给分离了，只需要用卡特兰数算出 $(A,k)$ 的方案数即可。

AGC039F Min Product Sum

容易想到枚举行列的最小值，计算方案数的同时统计贡献。

从大到小枚举最小值，设 $dp_{k,i,j}$ 表示解决了 $\min\ge k$ 的 $i$ 行 $j$ 列，方案数乘上权值的总和。

转移可以枚举 $x,y$ 表示 $k-1$ 的行列数，但是转移系数不好算，复杂度也炸了。

考虑对于一组行列最小值怎么计算方案数。对每一种最小值分别容斥即可。

那么加入新的行列的时候顺便容斥一下就行了……然后发现行列此时就独立了……

还有另外一个做法。把计数变成要数矩阵对 $(A,B)$ 的个数，使得 $A$ 的任意一个格子都比 $B$ 同行同列的格子小或相等。

这又可以转化为对于任意一行或一列， $A$ 的最大值小于等于 $B$ 的最小值。

一开始那个 DP 的问题在于行列同时有限制，所以无法避免容斥。但是现在有两个矩阵，可以把限制拆到两边，就不需要容斥了。

从小到大枚举 $k$ ，设 $f_{k,i,j}$ 表示考虑了 $A$ 中 $\max<k$ 的行和 $B$ 中 $\min<k$ 的列，使得满足限制，且 $A$ 填了 $nm-(n-i)(m-j)$ 那些格子， $B$ 填了 $ij$ 那些格子，的方案数。转移就先枚举 $A$ 的行再枚举 $B$ 的列，发现刚好这样可以分开转移。（多试几次就试出来了？）

AGC053D Everyone is a winner

首先把 3,2,1 变成 2,1,0 。显然对于第 $i$ 个人，前 $i$ 题和后 $n-i$ 题分别降序排序。

考虑贪心。头铁地考虑贪心。

考虑寻找一些能用于贪心的性质。比如对于一个 $i$ ，在保证前 $i$ 题的总时间不变的情况下，能不能尽量把两个 1 换成一个 2 ？

这样对于 $<i$ 的限制是有利的，但是对于 $>i$ 的限制就是有害的了。

那么能否从大到小贪心，在保证 $>i$ 的位置没有死掉的情况下尽量增大前 $i$ 题的时间&& 2 的个数？

不能盲目增大前 $i$ 题的时间，否则后面可能就无解了。

然后我不知道题解是怎么想到的，所以我只能搬运题解。

设 $T'_i$ 表示，如果每个人都降序做题，前 $i$ 题的最小时间是多少。设 $T_i$ 表示第 $i$ 个人的前 $i$ 题在什么时间一定要完成。初始设 $T=T'$ 。显然 $T'$ 是凸的，差分 $\le 2$ 。

从 $n$ 到 $1$ 贪心，对于每个 $i$ ，优先让前 $i$ 题的总时间尽可能接近 $T_i$ ，然后放尽量多的 2 。如果无法 $\le T_i$ 那么无解，否则对于 $j\le i$ 更新 $T_j$ 。显然这样对以后的 $T_j$ 影响最小。

整个过程做完之后 $T_i$ 就表示第 $i$ 个人的前 $i$ 题的时间。

但是我们做 $i$ 的时候并没有考虑到是否会把 $j>i$ 给干掉。我们分类讨论一下（下用 $i[l,r]$ 表示 $i$ 在 $[l,r]$ 中做的题）：

$i$ 的所有 1,2 都放进前 $i$ 个题了，那么就是降序做题，有 $T'$ 的限制，一定合法。
$i$ 只有 2 ，那么可能无法恰好卡满 $T_i$ 。但是容易发现整个过程做完之后有 $T_i+2\ge T_{i+1}$ ，而 $i$ 后面也全是 2 ，所以一定合法。
$i$ 有 1 ，那么一定把 $T_i$ 卡满了。此时如果 $T_i=T'_i$ 那么容易发现一定合法，否则存在一个 $i_1>i$ 把 $T_i$ 卡小了。可以发现 $i[i+1,j]\in \{1,2\},i_1[i+1,i_1]\in \{0,1\}$ 。然后可以继续讨论一些东西，推出合法性。

综上，一定不会把 $j>i$ 干掉，这个贪心非常正确。最后模拟的时候用三条折线来维护 $T$ 即可。

AGC053E More Peaks More Fun

谢谢，有被自己蠢到。

对于一个排列，容易想到贪心策略：从左往右考虑，如果 $l_i<r_{i-1}$ 那么先 $l$ 后 $r$ ，否则以后的都先 $r$ 后 $l$ ，并且需要有 $l_j<r_{j+1}$ 。

先考虑全程 $r_i>l_{i+1}$ 的情况怎么计数。发现把 $r$ 最小的那个线段删掉之后序列仍然合法，所以只需要按 $r$ 从大到小加入线段即可。

否则可以枚举分段点的两个线段，然后类似的方法做。用前缀和优化。

ARC116F Deque Game

考虑 $K=1$ 的情况。此时根据 $n$ 的奇偶性，容易发现答案是 $\max(a_{m-0.5},a_{m+0.5})$ 或 $\min(a_m,\max(a_{m-1},a_{m+1}))$ 。

容易发现在 $n$ 是偶数时先手优于后手，否则后手优于先手。

那么推到 $K$ 更大的情况，容易发现先手总是选择偶数长度的序列以获得更好的收益。都为奇数之后答案就是每个序列的答案之和。

这是因为如果先手选择奇数序列，那么后手可以扳回原来的情况，所以一定不优。

ARC117F Gateau

我慢死了（（（

显然可以二分答案，不过二分答案有什么用？

注意到区间长度是 $n$ ，恰好为环长一半，所以取反之后仍然是环长一半。那么在二分答案之后可以把一半的限制转化到另一半。

现在的限制是对于 $i\in [0,n-1]$ ， $[i,i+n-1]$ 中的个数要在 $[a_i,b_i]$ 之中。

一颗草莓可以让任意一个前缀或后缀加一，但是并不知道有多少个是前缀，有多少个是后缀，有点不爽。

如果只有前缀操作呢？容易发现合法当且仅当左边的上界大于等于右边的下界，并且草莓个数大于等于所有下界。

假装知道有若干颗草莓用来前缀加一。那么维护 $(x,mn)$ 表示有 $x$ 个操作可以超过这里，和右边经过操作之后的上界至少要为 $mn$ 。当前位置能加就加，直到 $x$ 全部用完（即可以通过到下一个位置），或是这里的上界变为 $mn$ 。

不合法情况有两种：一是做的过程中出现某个位置的上界已经小于 $mn$ ，二是做完之后发现剩下的草莓不足以搞定所有下界。

但是注意到给前缀的草莓减一，最多使得剩下的下界加一，所以第二种情况只能代表左边的草莓个数过多。

同样，如果某个草莓个数是合法的，那么给左边多加一些也不会使得第一种情况发生，所以第一种情况只能代表左边的草莓个数过少。

那么就可以二分给前缀多少个，然后 $O(n)$ 判断。总复杂度 $O(n\log^2 A)$ 。

ARC118F Growth Rate

谢谢出题人教会我怎么在不骂出题人的情况下做完这一题（（（

维护一个多项式 $f$ ，支持：

得到新多项式 $F$ ，使得 $F(x)=\sum_{i=x}^m f(i)$ 。
得到新多项式 $F$ ，使得 $F(x)=f(kx)$ 。

通过维护点值，容易搞定第一种操作，但是第二种操作就比较麻烦。

但是注意到大部分都有 $k=1$ ，所以真正有用的第二种操作很少，所以可以无脑插值。

ARC119F AtCoder Express 3

观察一下，发现如果前面有一大段的相同字符，那么用另一种字符跳过去一定是最优选择。

那么说明任意时刻要考虑的字符数量应该不会太多，考虑建一个自动机来求出任意字符串对应的最短步数。

最后发现有用的状态只有 13 个：

A,AA,AAA,BA...A,AB ，人站在第一个位置。其中 A,AA,AAA 前面一格还会有个 B 。
上面 5 种状态取反得到另外 5 种。
?A ，其中 ? 表示既可以是 A 也可以是 B 。另外还有 ?B,? 。

手玩一下即可建出自动机，然后暴力做。复杂度 $O(13n^2)$ 。

ARC120F Wine Thief

先考虑 $D=2$ 的情况。我们需要求解 $(a,b)$ 的答案，其中 $a+b=n-3$ ，表示左边有 $a$ 个，右边有 $b$ 个，一共要选 $K-1$ 个，两边独立。

$a=0$ 或 $b=0$ 就是一个简单的组合数。否则，考虑把两边拼接在一起，那么少数了 $a$ 的右边和 $b$ 的左边都选了的方案。那么令 $a,b,K\gets ^- 2$ ，然后接着数。

发现在处理前缀和之后即可 $O(1)$ 算出答案。

然后考虑 $D$ 更大的情况。经过随机尝试，发现可能还是拼接的方式最有效。但是现在少数了的方案太冗杂了，所以改变思路，拼接的时候在中间多加 $D-1$ 个空格子，于是就多数了这 $D-1$ 个中有选的方案。

令 $G(n,K,i)$ 表示 $n,K$ ，强制选 $i$ 的方案数。那么发现上面的思路刚好会把 $G(n,K,i)$ 递归到 $G(n-D,K-1,?)$ 。写得更清晰一点，有

\[G(n,K,i)=F(n-D,K-1)-\sum_{j=1}^{D-1} G(n-D,K-1,i-j) \]

其中 $F(n,K)$ 表示总方案数，$i-j\le 0$ 或 $i-j>n-D$ 时 $G=0$ 。

发现除了边界的 $2D$ 个位置以外，每个位置都从恰好 $D-1$ 个位置转移过来，所以整体加常数可以打 tag 。边界的 $2D$ 个位置其实只需要考虑前 $D-1$ 个位置（因为后面是对称的），它们转移的位置个数不同，所以需要特殊处理。

那么状态可以被写成 $(A,B,t)$ ，其中 $A$ 是主多项式， $B$ 是给前后额外调整的多项式， $t$ 是每个位置都要加 $t$ 。一次迭代带来的变化是给 $A,B$ 都乘上 $\sum_{j=1}^{D-1} x^j$ 、给 $t$ 乘 $D-1$ 再加一个常数，给 $B$ 加上 $t$ 乘某个常多项式。当 $|B|>2|A|$ 的时候重构。

那么就是倍增+分治 NTT 。

ARC122F Domination

又被网络流打爆了。

显然我们只需要考虑外层轮廓线上的红色石头，于是把二维转成类似一维的情况。

先考虑 $K=1$ 的情况。一个蓝色石头如果想要覆盖某个区间的红色石头，那么要把 $x$ 坐标移到右端点位置，把 $y$ 坐标移到左端点位置。这么说来左右端点其实比较独立，贡献也很独立。

那么就可以用路径来描述一种方案：新建虚点 $n+1$ ，如果一个蓝色石头 $i$ 覆盖了区间 $[l,r)$ ，那么就是走了 $l\to i\to r$ 的路径。代价可以被写在边上。

当然如果这么做那边数就起飞了。代价可以被写成 $\max(0,RY_l-BY_i),\max(0,RX_{r-1}-BX_i)$ ，那么可以把它写在坐标轴上。

在 $y$ 轴上，向下走需要 1 的代价，向上走不用代价；在 $x$ 轴上向右走需要代价而向左走不用。原点不会连接两个轴。

于是路径就变成 $(0,RY_l)\to (0,BY_i)\to (BX_i,0)\to (RX_{r-1,0})$ 。然后再把 $(RX_{r-1},0)\to (0,RY_r)$ 这条边补上就完美了。

检查一下，不会出现奇怪路径的情况，所以 $K=1$ 的时候就转化为最短路。

发现 $K>1$ 的任何一个合法方案都可以被拆成 $K$ 个 $K=1$ 的方案，所以直接变成费用流即可。

AGC054F Decrement

因为要计数，而 $A,B$ 范围实在太大，所以观察一下之后就可以把 DP 丢掉了。（不过我好像总是摸不清什么时候该丢掉）

那就只能~~复读题解~~找操作性质了。

设 $a_i,b_i$ 分别表示 $A_i,B_i$ 的变化量， $b_0=b_n=0$ 。发现对于一个 $i$ ， $a_{i},b_{i-1},b_i$ 在一次操作中要么不受到影响，要么有恰好两个 -1 。

于是可以推出 $a_{i},b_{i-1},b_i$ 相加为偶数，并且 $max\le sum/2$ 。

然后找上界。观察一下 $a_i<A_i$ 的原因，其中之一肯定是 $B_{i-1},B_i$ 太小；但是 $b_i$ 也不一定能取到 $B_i$ ，这是因为 $A_i+B_{i-1}$ 或 $A_{i+1}+B_{i+1}$ 太小。

那么可以先把 $B$ 往下砍，然后再把 $A$ 往下砍。显然砍完 $A$ 之后不会再需要砍 $B$ 。

现在 $m$ 能不能取到 $\sum A_i$ 的上界呢？发现还是不行，因为对于 $A_i=B_{i-1}+B_i$ 的位置，如果顶到上界，就把 $b_{i-1},b_i$ 都固定了，于是奇偶性都确定了，然后其他位置如果都顶到上界，那么奇偶性就可能出现矛盾。

不过对于这样的位置，最后一定会取 $a_i=b_{i-1}+b_i$ ，所以两边的方案非常独立。我们可以假装 $B_i=0,A_i=B_{i-1}$ 去做 $[1,i]$ ，然后假装 $B_{i-1}=0,A_i=B_i$ 去做 $[i,n]$ 。也就是在这些位置把序列切开，然后每一段分别做，最后 $m$ 就是每一段相加，方案数就是每一段相乘。

现在考虑能否取到上界。不妨从左边开始，令 $b_1=B_1$ ，然后一路推到右边。推的过程中 $a$ 全部顶到了上界，而 $b$ 只有可能比上界小 1 。但是做到 $a_n$ 的时候可能 $b_{n-1}$ 比上界小 1 ，于是就挂了。

冷静分析一下，发现 $\sum A_i$ 为偶数的时候不会出现上面这种情况，而 $\sum A_i$ 为奇数的时候肯定至少要减一。给 $A_n$ 减一即可。

所以只需要在 $\sum A_i$ 为奇数的时候判断每个位置减一之后能否顶到上界。

但是一个位置减一可能会带来很多 $B_i$ 的变化，不太好处理。所以最简单的方法是两边往中间做一个 DP ，减一的时候直接合并两边的信息。

ARC123D Inc, Dec - Decomposition

注意到通过整体加减，一定可以把最优解调整出一个 0 来。不妨假设是 $B_k=0$ 。

那么会发现， $B_k$ 之后的 $B$ ，都会贪心地选择能选的最小的数。即 $B_i=B_{i-1}+\max(0,A_i-A_{i-1}),i>k$ 。因此 $C_i=C_{i-1}+\min(0,A_i-A_{i-1}),i>k$ 。然后发现 $i\le k$ 的情况恰好也是完全一样的。

因此， $B,C$ 的差分值已经确定了，只需要确定 $B_1$ 即可确定所有数。

然后把代价写成关于 $B_1$ 的函数即可。

ARC123F Insert Addition

容易发现，我们最大的问题是计算 $a,b$ 中间能搞出多少个数。

经过观察，发现题目的操作和 SB 树完全一致，所以用莫比乌斯反演+扩欧可以 $O(\sqrt n\log n)$ 算出来。

既然有了 SB 树， $xa+yb$ 中 $y/x$ 的值就也单调了。通过二分这个值可以 $O(\sqrt n\log^2 n)$ 算出任意一个位置 $B_k$ 。

题解说 $B_k,B_{k+1}$ 就可以推出 $B_{k+2}$ ，我好像不太会。但是只要知道 $B_L$ 的 $(x,y)$ 就可以通过 SB 树二分来快速找到 $[L,R]$ 中所有数。

最后复杂度 $O(N+(R-L))$ 。

ARC125F Tree Degree Subset Sum

又被打爆了 /kk

树的具体形态显然用处不大：只要 $\sum d_i=2n-2$ 都可以构造出一棵合法的树。

我们的主要问题出在多了一维 $x$ 。因为什么性质也找不出来，尝试把 $x$ 这一维消掉。

先把所有 $d_i$ 都减掉 1 ，那么 $\sum d_i=n-2$ 。我们尝试证明：对于总和 $y$ ，设 $m(y),M(y)$ 分别是最小和最大的 $x$ ，那么 $x\in [m(y),M(y)]$ 都有合法方案。

我们的证明主要和 0 的个数 $z$ 有关。因为 $m(y)$ 必然一个 0 都没选，而 $M(y)$ 选了 $z$ 个 0 ，所以只要 $M(y)-m(y)\le 2z$ ，就可以通过调整 0 的个数构造出每个 $x$ 。

然后我也不知道怎么注意到的。发现对于任意一个集合 $S$ ，都有 $-z\le y(S)-x(S)\le z-2$ ，所以 $-z\le y-M(y)\le y-m(y)\le z-2$ ，所以 $M(y)-m(y)\le 2x-2$ ，然后就证完了。

ARC126F Affine Sort

又被打爆了 /kk

根据 stolz 定理或者感性理解，设 $g(K)$ 为 $c=K$ 时 $(a,b)$ 的个数，那么答案就是 $\frac 1 3 \lim_{K\to \infty} \frac{g(K)}{K^2}$ 。

一个关键转化：由于 $K$ 非常大，与其关心 $(aX_i+b)\bmod K$ 不如关心 $\frac a K X_i+\frac b K$ 的小数部分。这样令 $a=a/K,b=b/K$ ，就可以把 $a,b$ 都看作 $[0,1)$ 之间的实数了。

然后非常自然地想要消掉 $b$ 这一维，只考虑 $a$ 需要满足什么条件。显然是要求 $\{aX_i\}$ 在 $[0,1)$ 这个圆环上顺序排列。

转化一下顺序排列的条件，就是相邻两个数的顺时针距离之和恰好为 1 。然后维护分段函数即可求出 $a$ 的合法区间，然后再对每个区间把合法的 $b$ 的长度积分出来即可。

ARC128F Game against Robot

按照机器人吃的顺序排序，那么可以得到一个贪心策略：从后往前，每次往堆里加入两个元素，然后弹出最大的元素。结果就是弹出的元素之和。

因为只和大小关系有关，可以枚举一个 $lim$ ，然后把元素序列变成 01 串。

现在相当于是左边的 0 和右边的 1 匹配，但是特殊情况是同时间加入的两个元素无论 01 顺序都可以匹配。

用最大前缀和什么的搞一搞，那么考虑进特殊情况之后，我们就只关心最大前缀和除以 2 下取整。这还是可以翻折法乱搞。

ARC131F ARC Stamp

口胡。

考虑如果 $S$ 和 $T$ 完全对不上，那么 $T$ 要长成什么样子才能变过去。

容易发现 $T$ 中不能出现 22 和 13 ，且 $T$ 开头是 1 ，结尾是 3 ，并且这就是充要条件。变过去的次数是 $|T|-occ(\text{12})-occ(\text{23})$ ，并且这很容易把贡献拆到每一个位置。

那么先把 $T$ 里的 22,13 的中间切开，分别统计每一段，最后合并。

把所有 $S$ 和 $T$ 不同的位置标出来，那么显然最优方案就是每个位置往前找到第一个 1 ，往后找到第一个 3 ，然后把相交的段合并，就得到最终要改变的段。

我们考虑先钦定每一个要改变的段，然后看一个段是否合法。显然合法要有四个条件：

段内有至少一个错的位置。
第一个错的位置之前只能有一个 1 。
最后一个错的位置之后只能有一个 3 。
相邻两个错误之间不能存在子序列 31 。

对着这四个条件构造一个 DFA ，然后从左往右确定 $S$ 与 $T$ 不同的位置，大力 DP 应该就行了。

ARC132F Takahashi The Strongest

先把另外两个人的策略固定下来，然后考虑自己有哪些不合法的策略。显然，当那两个人在这一局不同时自己怎么出都可以，否则会 ban 掉胜利的那种出法。

那么先把 PRS 置换成 SPR （分别设为 123 ），然后可以考虑一种状态是 $4^k$ 的卷积：如果 $a_i=b_i$ 那么 $c_i=a_i$ 表示禁止使用 $c_i$ ，否则 $c_i=0$ 表示什么都没有禁。

显然，只要能求出 $c$ ，那么就可以再对每一位做一个变换得到答案。

注意到如果把 123 分别对应到 $1,2,4$ ，那么这个卷积就变成 and 卷积了。又因为在 and 卷积的过程中还是只有 $0,1,2,4$ 这四个位置有值，所以对应回 $0,1,2,3$ 即可。复杂度 $O(k4^k)$ 。

ARC133E Cyclic Medians

显然应该枚举 $lim$ 变成 01 串。一旦某一次同时出现两个 0 或者同时出现两个 1 ，那么答案就和初始值无关了。

从后往前枚举最后一次相等的位置，并查集维护，……然后发现贡献关于 $lim$ 是非常诡异的多项式，没法做。

但是枚举 $lim$ 这个思路是确定无疑的。所以注意到 $>lim$ 和 $<V-lim$ 是对称的，所以所有 $lim$ 的情况中结果是 1 的恰好占一半。（差不多是这样吧。）

然后就只需要考虑不存在相等位置的情况了。这个随便算算即可。

ARC135E Sequence of Multiples

水平不行，完全不会。

设 $B_i=A_i/i$ ，不难得到递推式 $B_{i+1}=\lfloor iB_i/(i+1)\rfloor +1 = B_i+1-\lceil B_i/(i+1)\rceil$ 。显然 $B_i\ge B_{i+1}$ ，而当 $B_i\le i+1$ 时 $B$ 就退化为常数序列。进一步，还可以发现 $B_i-B_{i+1}=\lceil B_i/(i+1)\rceil-1$ 也是不增的。

显然应该考虑 $B$ 会经过多少步之后变为常数。因为 $A_n-A_{n-1}\le n$ ，所以不难证明 $A_n\le X+n^2$ ，所以 $B_n\le X/n+n$ 。令 $n=\sqrt X$ ，即得 $B_{2n}\le B_n\le 2n$ 。

这个 bound 还不足以跑暴力，所以考虑利用 $B_i-B_{i+1}$ 不增的性质。令 $n=X^{1/3}$ ，则 $B_n/(n+1)\approx n$ ，因此 $B_i-B_{i+1}$ 只有 $O(X^{1/3})$ 种不同的取值，这就可以跑暴力了。

ARC135F Delete 1, 4, 7, ...

正着做显然没什么前途，应该倒推：设 $f(x)=\lfloor 3x/2\rfloor + 1$ ，那么 $f^K(x)$ 就是最终在第 $x$ 个位置的数。

观察数据范围，发现 $K>40$ 时最后就已经没剩几个数了，可以暴力。只需要解决 $K$ 较小的情况。

显然只有 $x$ 的二进制最低 $K$ 位比较有用，更高位对 $f^K(x)$ 的贡献是确定的。因此 $O(2^KK)$ 的算法是显然的。

$K$ 也没多大，meet in the middle 一下即可。

ARC136E Non-coprime DAG

考虑两个数什么时候可达。发现偶数是个好东西，而只要 $x$ 不是偶数，$x+f(x)$ 就一定是偶数，其中 $f(x)$ 是 $x$ 的最小质因子。

不难把每个数变成一个区间，两个区间无交则可达，有交则……不可达。后者分类讨论一下发现是对的，即使是 $\gcd(x,y)\ne 1$ 的特殊情况也成立。

因此选出来的区间必须两两有交，枚举一个交点即可。

ARC137F Overlaps

先变成离散情况，然后顺序决定每个点是左端点还是右端点，是右端点时要给方案数乘上可选的左端点个数。

考虑每个右端点乘的数 $x_i$ ，发现 $x$ 只需要满足 $x_i\ge x_{i-1}-1$ 和 $x_n=1$ ，就能和左右端点的方案一一对应。因此只需要对 $x$ 做统计即可。

$x$ 不是有序的，但只要对 $x_i\ge x_{i-1}-1$ 做容斥，那么每一段就都是有序的，分治矩阵乘法维护多项式即可。

ARC138E Decreasing Subsequence

水平不行，完全不会。

如果使用经典手段，从小到大维护当前还有几个数没有被用过，很容易做到 $O(n^3)$ ，但看不出怎么优化到 $O(n^2)$ 。

建图，连边 $i\to a_i-1$ ，那么会得到若干条链。在其中 $K$ 条链中分别选一条边得到所需的下降子序列，剩下的问题就只是计算把 $i$ 个点拆成 $j$ 条链的方案数了。

你说得对，但不知道是怎么想到的。

ARC139F Many Xor Optimization Problems

按顺序考虑每个数显然是没有前途的，应该考虑线性基。

一个重要的观察是，很多不同的线性基会得到相同的方案数。只要确定了线性基的大小 $K$ ，无论里面具体放了哪些数，序列 $A$ 的方案数都是 $\prod_{i=0}^{K-1} (2^n-2*i)$ 。这可以通过矩阵的行秩与列秩相等来得到。

线性基到最大 xor 值的映射是显然的。然后就推式子即可。

ARC140E Not Equal Rectangle

\[(\lfloor i/p\rfloor \cdot \lfloor j/p\rfloor + i + j) \bmod p \]

ARC141F Well-defined Abbreviation

基本推出来了，可惜还是稍微麻烦了一点点。

从简单的情况入手：直接考虑某个 $S_i$ 会不会是坏串。如果 $S_i$ 包含 $S_j$ ，而只通过删小串无法把 $S_i$ 消除，就做完了。否则可以把删除 $S_i$ 的操作拆解为更小的操作，所以整体不存在坏串当且仅当不考虑 $S_i$ 时不存在坏串，可以不管 $S_i$ .

下一步应该考虑两个串有共同的前后缀的情况，即 $S_i=A+B,S_j=B+C$ 。这时候直接考虑 $A+B+C$ ，显然既可以得到 $A$ 也可以得到 $C$ 。而由于 $S_i,S_j$ 都无法进一步操作，自然有 $A,C$ 无法进一步操作，因此只要 $A\ne C$ 就存在坏串。而如果总是有 $A=C$ ，那么就可以把满足条件的删除 $S_j$ 的操作换成删除 $S_i$ ，最终使得每一步都在删除最靠左的可删除的子串，从而得到唯一性。

ARC142F Paired Wizards

口胡。

记 0 表示攻击， 1 表示 +1 。

除掉 01 10, 00 11 这两种比较麻烦的情况以外，剩下的都是定住了一个巫师的操作，而另一个巫师随意操作。此时两个巫师是独立的。

显然每个巫师都会在一个前缀选择 1 ，后缀选择 0 ，可以 $O(n^2)$ 分别枚举分界点。

然后考虑 01 10 。如果不考虑 01 10 之间的贡献，那么在每个位置，选择 01 和选择 10 带来的收益之差是相同的。但如果 01 和 10 分别选了 $x,y$ 个，那么还有额外的 $xy$ 的贡献。因此可以贪心确定 01 和 10 分别选几个，而不需要关心具体的位置。

最后是 00 11 。注意到 00 11 与 01 10 是完全独立的，因此也只需要贪心地前缀选 11 后缀选 00 即可。这可以在 $O(n^2)$ 枚举分界点时顺便把这个的分界点也维护出来。

ARC143F Counting Subsets

简单分析一下计算凑出每个数的方案数的过程，发现就是初始有 $a$ 个 $1$ ，然后每次翻转一遍贴在后面，并且把重合的 $1$ 变成 $2$ 。

由于 $>n$ 的数允许有多种方案，因此当长度超过 $n$ 之后，还可以在 $n$ 所在的一段 $1$ 里面再选一个数。所以给答案的贡献是最后一段 $1$ 的长度。

枚举 $a$ ，枚举 $n$ 前面的 $2$ 连续段个数，然后对 $O(\log n)$ 次翻转做 dp 。dp 大概是可以前缀和优化一下，所以每次翻转的 dp 复杂度都是 $O(n)$ 。连续段个数不超过 $n/a$ ，因此总复杂度 $O(n^2\log^2 n)$ 。

ARC144F Arithmetic Sequence Nim

把所有数按照 $\bmod m$ 分类，那么不难发现，对于同一类数，更大的数的 NIM 也会更大。

因此，如果存在 $0<x<m$ 使得 $\text{NIM}(x)>0$ ，那么所有 $km+x$ 的 NIM 都 $>0$ ，这就会导致所有 $km+x+a$ 的 NIM 都 $=0$ 。

有了这样一组基准态之后，就可以递推获得所有 $km+x+2a,km+x+3a$ 的 NIM 值，都形如 $0,1,2,3,3,\cdots$ ，除非碰到下一个全都是 NIM=0 的类。

分类讨论一下把所有 NIM=0 的类挑出来即可。

ARC145E Adjacent XOR

我想了个有点麻烦有点抽象的从前往后推操作的做法，不太聪明。

第一反应肯定是从 $n$ 到 $1$ 倒着做。但是倒着做的一个问题是，想异或的数的位置可能很靠前，那么把它拉过来就需要很多次操作。

但是注意到差分的逆操作是前缀和，而前缀和就可以一步操作把很靠前的数拉过来了。

因此把操作顺序也反过来，然后从后往前做，就可以构造出来了。

ARC145F Modulo Sum of Increasing Sequences

令 $B_i=A_i+i$ 变成不可重复地选 $n$ 个，然后生成函数，然后单位根和 FFT ，然后通过合并差不多的项把复数都合成有理数。

ARC146F Simple Solitaire

感觉和 ARC137F 挺像啊，又是个容斥矩阵乘法分治 NTT 。

ARC148E ≥ K

口胡。

先加入一个 $\infty$ ，把数链变成数环。

以 $K/2$ 作为分界线，把所有数分为小数和大数两种。那么小数两边必须都是大数，且只要每个小数两边都合法就全都合法。

从小到大考虑每个小数，同时加入可用的大数，那么每次就是任选两个大数放在左右，并把他们合在一起。因为是从小到大考虑，所以合并之后也不需要关心它的值是多少了。

ARC159E Difference Sum Query

直接计算绝对值肯定是麻烦的。但我们可以把贡献拆开，每分割一次就给区间的端点加一，那么答案就差不多是出现的区间个数了。具体来说，每个区间的贡献是它在询问区间里的端点个数（差不多这样）。

只有 $O(\log n)$ 个区间没被完全包含，因此只需要快速计算一个长度的区间会被分割出几个小区间即可。

这不就是区间长度吗，让每个区间与它的分割点一一对应就好了（

ARC160F Count Sorted Arrays

一个排列，只要对于每个 $i$ ，$\le i$ 的 mask 被排好序了，那么这个排列就是合法的。

一个 mask 只会经过 $O(n^2)$ 步 swap ，因此 $\tilde O(2^n)$ 维护所有被排好序的 mask 是简单的。接下来的问题是怎么实时统计路径数。

题解证明了即使同时考虑所有排列，有效的 swap 也只有 $O(n^2)$ 个，因此只需要对这 $O(n^2)$ 次操作重新统计路径数即可。

ARC161E Not Dyed by Majority (Cubic Graph)

不难证明一定有解：因为操作是从 $\{0,1\}^n\to \{0,1\}^n$ 的映射，而这个映射显然不是单射，因此也不是满射。

不难想到 spj 怎么写：就是一个简单的 2-sat 。

尝试构造，造不出来。尝试随机，发现随出来了，做完了。证明挺妙，但不想写了。

ARC161F Everywhere is Sparser than Whole (Judge)

最大密度子图是简单的，二分答案之后用最大权闭合子图的方式转化为最小割，发现是个二分图，直接跑匹配即可。

因为只关心是否 $\ge D$ ，所以就令每个点的流量为 $D$ ，跑匹配。如果不存在完美匹配，说明存在密度 $>D$ 的子图，就做完了。

否则，根据完美匹配可以把每条边定向，每个点的出度都恰好为 $D$ ，得到一个有向图。不难发现完美匹配与定向方案一一对应。由于两个完美匹配的 xor 会得到若干个环，因此两个定向方案一定可以通过若干次改变环的方向来转换。

如果手上这个有向图不强连通，那么任意一个没有出度的强连通块都合法。否则不难证明所有合法的定向方案都强连通，一定找不到合法子图。

ARC162F Montage

手玩，手玩，手玩，发现把没有 $1$ 的行列删掉之后 $1$ 就必须形成一个双阶梯的形状，直接数即可。

ARC163F Many Increasing Problems

口胡。

考虑 Increasing Problems 的无脑 dp 维护凸函数做法，就是每次把两个 $a_i$ push 进去，然后 pop_max ，最终答案就是 $\sum a_i$ 减掉留在堆里的所有元素。

对每个 $s$ 把数按照 $\ge s$ 和 $<s# 变成 01 ，那么每次就是加入一个左括号或加入一个右括号，对答案的贡献是未被匹配的左括号个数（差不多这样）。

对每个位置分别计算这里放了左括号且被匹配了的概率，用卡特兰数得到一个关于 $p(1-p)$ 的多项式，其中 $p$ 是加入左括号的概率。

处理一下之后可能就变成幂和了。

ARC164F Subtree Reversi

两个人都想占奇数层的点，不想占偶数层的点。

如果一开始有奇数的点，贪心依次拿掉就好。

如果此时只剩一条链，那么先手每拿一个偶数，后手就拿掉奇数，于是先手一个奇数都拿不到。只有当树有分叉时，先后手依次一路拿到分叉点，此时先后手转换。

手玩一下，发现先手选择最短的链开始拿好像就是最优的。发现这就是在跑长剖，不难证明正确性。

AGC055D ABC Ultimatum

做 agc 就像大海捞针。

把 AB, BC, CA 分别看做三种括号匹配，那么一个合法方案需要 $2n$ 个括号匹配。设 $f_A,f_B,f_C$ 分别表示 AB, BC, CA 会“浪费”掉几个字符，或者说 A,B,C 分别有几个匹配不到右括号，那么 $f_A+f_B+f_C\le n$ ，否则无解。

然后是魔术：第 $i, i+f_A, i+f_A+f_B$ 个 A,B,C 作为一组即可。

AGC055E Set Merging

快做出来了，但没完全做出来。

一次操作显然就是把左边的 $L$ 赋给右边，把右边的 $R$ 赋给左边，而原先左边的 $R$ 和右边的 $L$ 消失。

可以把这个过程想象为把几个特定的 $R$ 往左推和把特定的 $L$ 往右推的过程，那么操作次数就是总的移动距离减掉一次操作两个的次数，即逆序对个数。

可惜，还要判无解：除了这几个特定的 $L$ 和 $R$ ，其他数可能会破坏这一过程。

那么就要用到题解的更为精简的描述：一次操作就是 swap 相邻两个位置，$L,R$ 分别是后缀最小值和前缀最大值。然后就只需要判断是否存在合法排列即可。

AGC055F Creative Splitting

真的假的，我咋好像做出来了。

尝试从前往后贪心，发现不行：比如开头是 1 1 3 ，那么第二个 1 就必须屈居第二。

尝试从后往前贪心，发现可以。每个数都接在能接的最长的串前面就行。

显然状态数只有 ${n+K\choose n}$ ，可惜还是跑不过去。

尝试算出到达一个状态的方案数。如果把所有序列放在一起得到一个 $n\times K$ 的矩阵，那么每次就是把某一行向左延伸一格，方案数是上面那行的长度减掉这行的长度。

发现可以把每一列视为独立的，每次就是往某一列下面加一个数。于是一个状态的方案数就是先把列打乱，然后 $m!/\prod c_i!$ ，其中 $c_i$ 是第 $i$ 列的数字个数。

下面就是推式子统计答案了。

ARC165E Random Isolation

把每一步操作的贡献放在相应的子树上。

随机一个排列表示抽取点的顺序，一个子树被操作当且仅当子树内的点比子树旁边的点的抽取时间都晚。大力树形 dp 即可。

ARC166F Tangent Addition Formula

我觉得这题有点太数学了。

ARC167E One Square in a Triangle

不妨假设原点是三角形顶点之一。设三角形的一个点是 $(a,b)$ 。

根据点到直线的距离公式，如果另一个点是 $(x,y)$ ，三角形的面积就是 $|ax-by|/2$ 。

令 $ax-by=1$ ，此时 $(x,y)$ 处在最接近直线的整点上，取到面积 $1/2$ ，但三角形内一个正方形也没有。

不妨就选离 $(x,y)$ 最近的正方形，令 $x'=x+1,y'=y-1$ ，则 $(0,0),(a,b),(x',y')$ 的面积是 $(1+a+b)/2$ 。简单分析一下发现三角形内确实只有唯一一个正方形。

$ax-by=1$ 有解当且仅当 $\gcd(a,b)=1$ 。枚举一下就行。

写个暴力发现做不出来的 $S$ 只有 $1,2,3,5,7$ ，而它们确实是无解的。

ARC167F Tree Tree Tree

狗都不写.jpg

显然我们只关心 $dist(i,j)$ 的分布。不考虑 $p_K=a$ 的限制，这个分布还挺好描述的：设 $f_n(x)$ 表示 $n$ 个点的距离分布的生成函数，那么 $f_{n}(x)=f_{n-1}(x)(n-1+2x)+1$ 。最后就是 $f_n(x)$ 和 $h(x)$ 做减法卷积，其中 $[x^k]h(x)$ 是长度为 $k$ 的链的期望权值。

然后考虑 $p_K=a$ 。可以另外设 $g_n(x)$ 表示 $n$ 个点到 $a$ 的距离分布的生成函数，则 $g_a(x)=a-1+xf_{a-1}(x),g_n(x)=g_{n-1}(x)(n-1+x)$ 。做到 $K$ 的时候把 $g$ 加进 $f$ 里。

$f$ 可以分治 NTT 做；不同的 $a$ 仅仅是导致 $g$ 的初值不同，减法卷积也可以用分治 NTT 处理。感觉已经成了 ARC 的常用套路了。

ARC168E Subsegments with Large Sums

共有三个维度：从左往右做到第几个数字、分出了几个段、分数是多少。无论在哪一维 dp 都需要维护另外两个维度，复杂度就 $n^2$ 了。出路只能是发现某个凸性，从而用维护凸函数或直接 wqs 二分的方式解决掉一维。

把每个极短的 $sum\ge S$ 的段拿出来，那么就是要选出尽可能多的两两不交的段，使得 $\sum(len-1)\le n-K$ 。

盲猜一手，$\sum(len-1)$ 关于段数是凸的。证明是用 $p$ 段和 $p+2$ 段的方案凑出两个 $p+1$ 段的方案，因此 $2s_{p+1}\le s_p+s_{p+2}$ 。

ARC168F Up-Down Queries

我觉得这题有点太神仙了。

ARC169F Large DP Table

画一个 $n\times n$ 的表格，$A_i,X_i$ 写在左边，$B_j,Y_j$ 写在上面。从 $(i,j)$ 出发，每次 $A_i,B_j$ 哪边小就往哪边走，并获得相应的贡献。

显然走到的只会是从 $i$ 或 $j$ 开始的后缀最小值。用单调栈建一棵树，那就是分别从 $i$ 和 $j$ 往上跳。

考虑 $A_x$ 的贡献。$A_x$ 会被计入几次不是很好数，但 $\ge A_x$ 被计入的次数是简单的，就是 $j-y$ ，其中 $y$ 是第一个 $B_y<A_x$ 的位置。设 $cnt_x=j-y$ ，则 $A_x$ 的次数是 $cnt_x-cnt_{son_x}$ ，求和就是 $\sum A_x(cnt_x-cnt_{son_x})=\sum (A_x-A_{fa_x})cnt_x$ 。

对每个 $x$ 算一下所有 $(i,j)$ 的 $cnt_x$ 之和即可。这个就随便搞搞。

posted @ 2019-05-08 21:01 p_b_p_b 阅读(5771) 评论(1) 编辑收藏举报

刷新页面返回顶部

p_b_p_b

Dream It Possible

Atcoder刷题记录

ARC066C Addition and Subtraction Hard

AGC033C Removing Coins

AGC014D Black and White Tree

ARC063F Snuke's Coloring 2

ARC068F Solitaire

ARC078F Mole and Abandoned Mine

AGC001F Wide Swap

AGC003D Anticube

AGC003E Sequential operations on Sequence

AGC004C AND Grid

AGC004E Salvage Robots

AGC004F Namori

树

奇环

偶环

AGC005E Sugigma: The Showdown

AGC005F Many Easy Problems

AGC006C Rabbit Exercise

AGC006D Median Pyramid Hard

AGC006E Rotate 3x3

AGC006F Blackout

AGC007C Pushing Balls

AGC007E Shik and Travel

AGC007F Shik and Copying String

AGC008C Tetromino Tiling

AGC008D K-th K

AGC008E Next or Nextnext

AGC008F Black Radius

AGC009D Uninity

AGC009E Eternal Average

AGC010C Cleaning

AGC010D Decrementing

AGC010E Rearranging

AGC010F Tree Game

ARC070E NarrowRectangles

ARC070F HonestOrUnkind

AGC036F Square Constraints

ARC071E TrBBnsformBBtion

ARC071F Infinite Sequence

ARC072D Alice&Brown

ARC072E Alice in linear land

ARC072F Dam

ARC073E Ball Coloring

ARC073F Many Moves

ARC074E RGB Sequence

ARC074F Lotus Leaves

ARC075F Mirrored

ARC076F Exhausted?

ARC077F SS

ARC078E Awkward Response

ARC078F Mole and Abandoned Mine

ARC079D Decrease (Contestant ver.)

ARC079E Decrease (Judge ver.)

ARC079F Namori Grundy

ARC080F Prime Flip

ARC081F Flip and Rectangles

ARC082E ConvexScore

ARC082F Sandglass

ARC083F Collecting Balls

ARC084D Small Multiple

ARC084E Finite Encyclopedia of Integer Sequences

ARC084F XorShift

AGC030C Coloring Torus

ARC103D Robot Arms

ABC134F Permutation Oddness

AGC041F Histogram Rooks

AGC043C Giant Graph

AGC043D Merge Triplets

AGC044D Guess the Password

AGC044E Random Pawn

AGC045D Lamps and Buttons

AGC045E Fragile Balls

AGC045F Division into Multiples

AGC046D Secret Passage

AGC046E Permutation Cover

World Tour Finals 2019 C Triangular Lamps

AGC047F Rooks