Curve learning1

Curve Learning

希望能够从数学上更深入地了解一些曲线的一些性质吧，之前遇到ECC只会调包属实有点难受了😢

这里我们讨论elliptic curve

参考材料

introduce

def

我们称满足Weierstrass方程Y²=X³+AX+B的点集为椭圆曲线(elliptic curve)

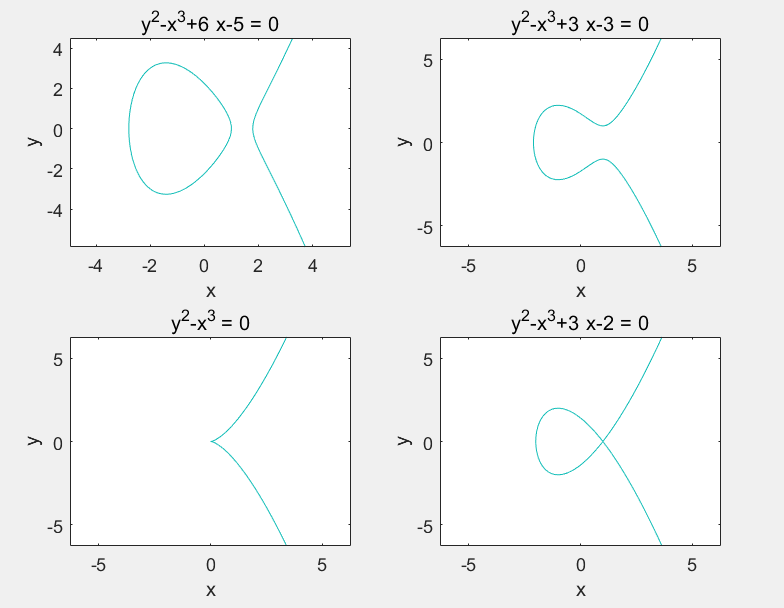
上图为常见的几种ec的形式，其中后两种被称为Singular curves

实际上到这里还是没有什么特别的，下面我们将在曲线上定义一种运算，为了让操作自洽，这里我们在集合中额外声明无穷远点O

add operation

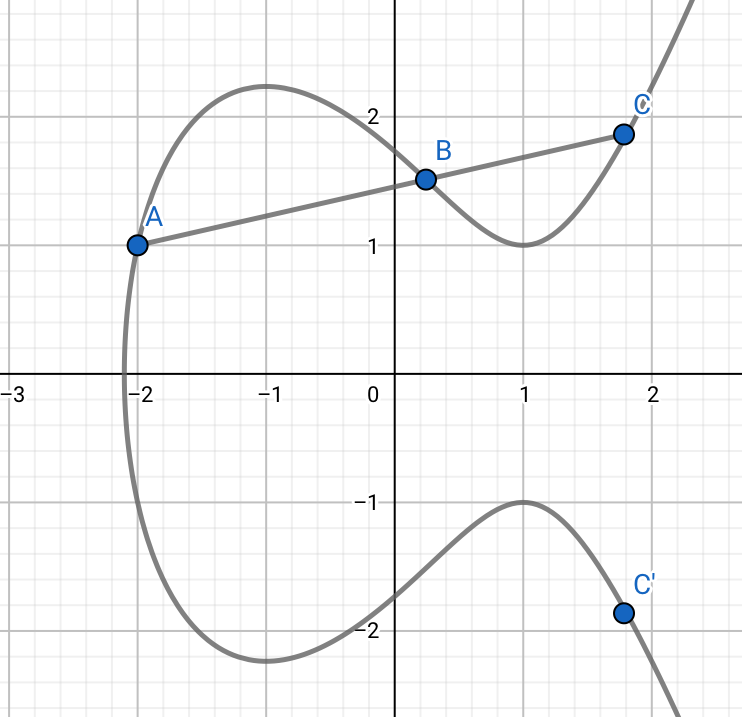
我们定义ec上的点加运算，A+B=C'，即相加两点的连线与曲线的另一交点关于x轴的对称

下面陈述点集和运算+形成的群结构

1)associativity

(A+B)+C=A+(B+C)，不剥蒜的话需要一点射影几何的知识，证明的方式可以参考proof

2)identity

集合中任意一点A，均有A+O=A，O+A=A

3)inverse

对于任意一点A，其关于x轴的对称即为逆元，A+A'=O

4)commutativity

对于集合中的两点A，B，AB与BA与ec的另一交点相同，故其对称后所得结果一致

上述性质说明ec和定义在其上的点加运算构成Abelian group

algebraic representation

y²=x³+ax+b

A(x_1,y₁)，B(x₂,y₂)，C(x₃,y₃)，A+B=C

不考虑含O的平凡情况，记\(λ=\left\{ \begin{matrix} \frac{y_2-y_1}{x_2-x_1}，A≠B\\ \frac{3x^2+a}{2y}， A=B \end{matrix} \right. \)

则x₃=λ²-x₁-x₂，y₃=λ(x₁-x₃)-y₁

elliptic curve in Galois field

在密码学上，希望使用离散的数学问题，则有了将ec放在有限域上的操作，相应的基于ecdlp产生了一系列的方案，如Elgamal，ecdas，ecdh等等，由于ecdlp相比数域上的dlp拥有更强的安全性(在同等长度密钥的情况下)由此得到了广泛的关注

我们记在有限域p上的点集为

E(p)={∞}∪{(x,y)∈p×p|y²=x³+Ax+b}

记r_i为y²=x³+Ax+b的根=>\(((r_1-r_2)(r_2-r_3)^(r_3-r_1))^2=-(4A^3+27B^2)\)

由此方程无重根=>\(4A^3+27B^2≠0\)，含有重根时我们称形成的ec是奇异的，此时取(r,0)和(r,0)相加使得我们的加法失效，于是我们在使用时避开判别式为0的情况

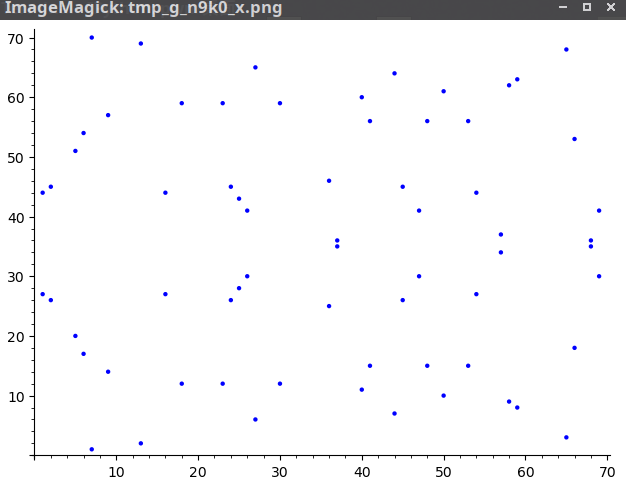
伽罗瓦域下的点仍然关于x轴对称，那么在域下ec上点的个数是多少呢？

这里需要用到Hasse定理

Hasse theorem

交换群E(F_p)中的点的个数满足#E(F_p)∈\([p+1-\sqrt{p},p+1+\sqrt{p}]\)

Hasse定理也称Hasse边界，说明了阶的取值范围，具有较大实用性，如我们需要得到一个2¹²⁸个元素的曲线群，那么我们p的选择就在128比特

attack

求解不同情况下椭圆曲线上的离散对数问题

general

离散对数问题有几个通用的基本解法

Pohlig-Hellman

Pollard-rho

Baby step giant step

import gmpy2

def bsgs(g,y,bound,p):
    m=gmpy2.iroot(bound,2)[0]+1
    dic={pow(g,m*j,p):j for j in range(m)}
    for j in range(m):
        t=pow(g,-j,p)*y%p
        if t in dic.keys():
            return dic[t]*m+j

下面主要讨论一些关于ec选择参数不当所带来的攻击

Singular Curve

前面有提及奇异曲线的条件，即方程有重根的情况，ec在选取的时候会规避这种此类曲线，原因是存在奇点使定义的点加运算出现问题

实际上即使我们额外补充定义使其自洽，此类曲线仍是脆弱的

对于y²=x³+ax+b

若满足4a³+27b²=0

=>y²=(x+r₁)²(x+r₂)

若r₁≠r₂

做代换t=x+r₁ =>y²=t³+r×t²

此类曲线可以通过映射φ将ecdlp问题转化到数域GF(p)上

φ=\(\frac{y+αx}{y-αx}\)(α²=r mod p)

证明过程可参考前文所给的参考资料2.10

若r₁=r₂

做代换t=x+r₁ =>y²=t³

做映射φ=\(\frac{x}{y}\)即可将ecdlp转化为数域上的dlp

Invalid point

对于一个对我们输入的点与私钥进行点加运算的Oracle，如果它不对输入点是否在曲线上进行检测，则我们可以进行Invalid point attack

注意到我们之前所列出的代数表达式中，对于点加运算并未涉及到参数b，如果运算开始前未检测点是否在曲线上则会造成在非要求曲线上将k与我们输入的点进行运算，这个时候如果我们控制输入点在一阶光滑的曲线上则可利用Pholig-Hellman算法进行ecdlp的求解

实际上不仅是椭圆曲线在其他曲线上都存在这样的攻击，所以在写曲线类时一定要记得Test the rationality of the point

SSAS attack

针对有理点群阶等于有限域大小的异常椭圆曲线，将ecdlp问题约化到有限域加法群的dlp，从而该类ecdlp问题存在多项式时间算法。通过构造映射将F_p上的ec提升到p-进域上，再通过模p的约化获得E(F_p)的离散对数解

references

代码实现

def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p,2),[ZZ(t)+randint(0,p)*p for t in E.a_invariants() ])
 
    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break
 
    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break
 
    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp
 
    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()
 
    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)

Mov attack

利用椭圆曲线上的双线性对映射将定义在有限域F_p上的ecdlp规约到有限域乘法群\(F_{p^k}\)上的离散对数问题，此方法在嵌入度k较小是有效。

补充嵌入度的定义

嵌入度是满足k≥2且椭圆曲线的阶，n|q^k-1的最小k

---

More attacks are waiting to be updated🏃