DES Learning
之前做题目的时候知道了DES使用的Feistel结构,比较有意思,顺带把DES的原理弄清楚一点
Feistel密码结构
简单来说Feistel结构是顺序地执行两个或多个基本密码系统,使最后结果的密码强度高于每个密码系统的结构
工作流程如下
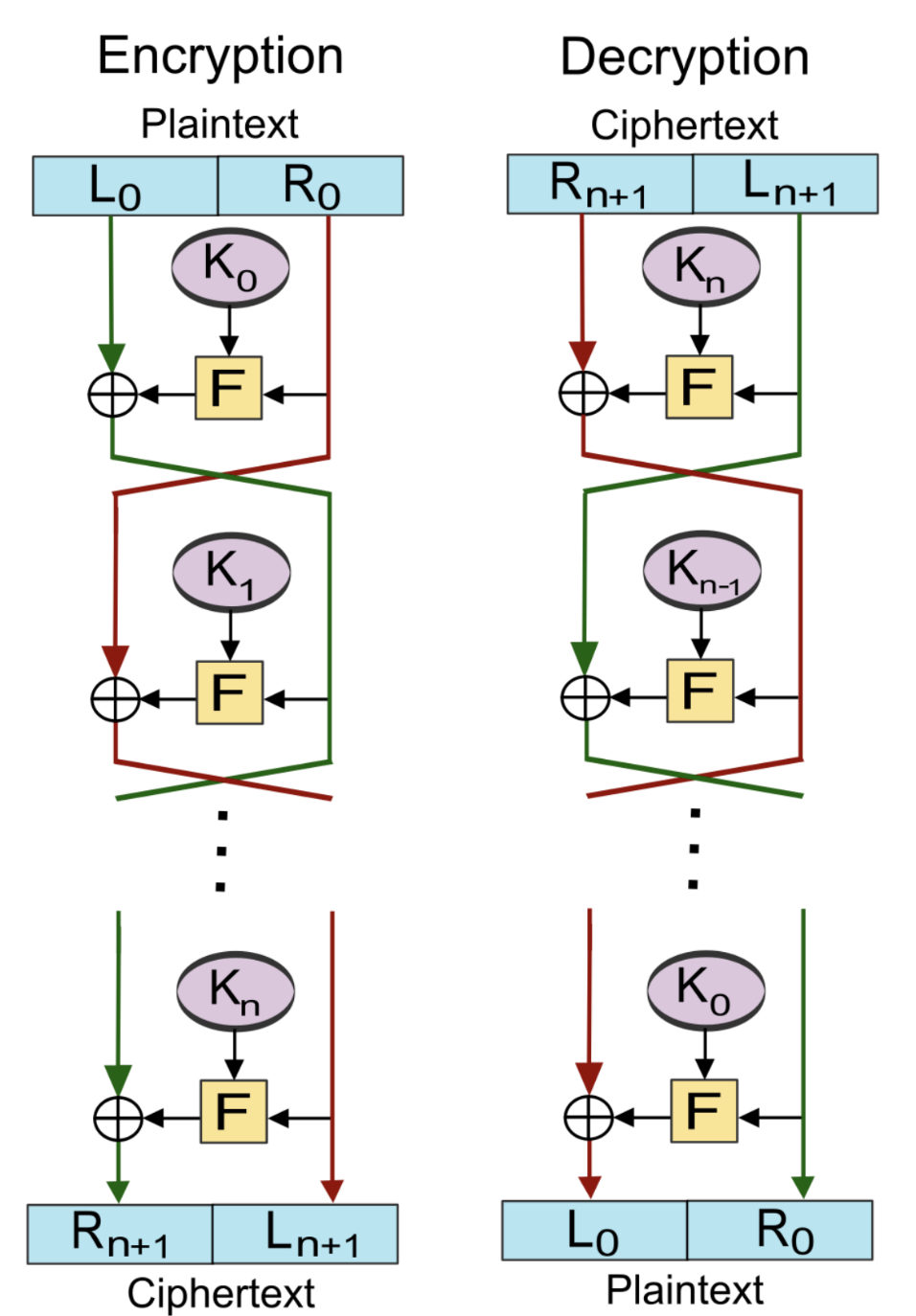
F为轮函数,K0~Kn作为轮密钥
对于Encryption
原始数据被分成长度相等的两部分(L0,R0)
每一轮的操作如下:
·Li+1=Ri
·Ri+1=LixorF(Ri,Ki)
最终输出(Rn+1,Ln+1)
相关参数与Feistel密码结构安全性
| 分组大小 | 分组越多安全性越高,但是会减慢加密速度 |
|---|---|
| 密钥长度 | 密钥越长安全性越高,同样会减慢速度,一般采取128bits |
| 加密轮数 | 轮数越多安全性越高,一般16轮 |
| 密钥扩展算法 | 同上 |
| 轮函数 | ··· |
一个很有意思的地方是使用Feistel体系的加密算法,解密与加密完全相同,只需把加密时所生成的密钥组倒置即可
DES算法
算法概述:
DES(Data Encryption Standard)算法是一种采用64bits的密钥(56位参与运算,其余八位为校验位)对64bits的分块进行加密的密码体制
下面是DES的Feistel结构
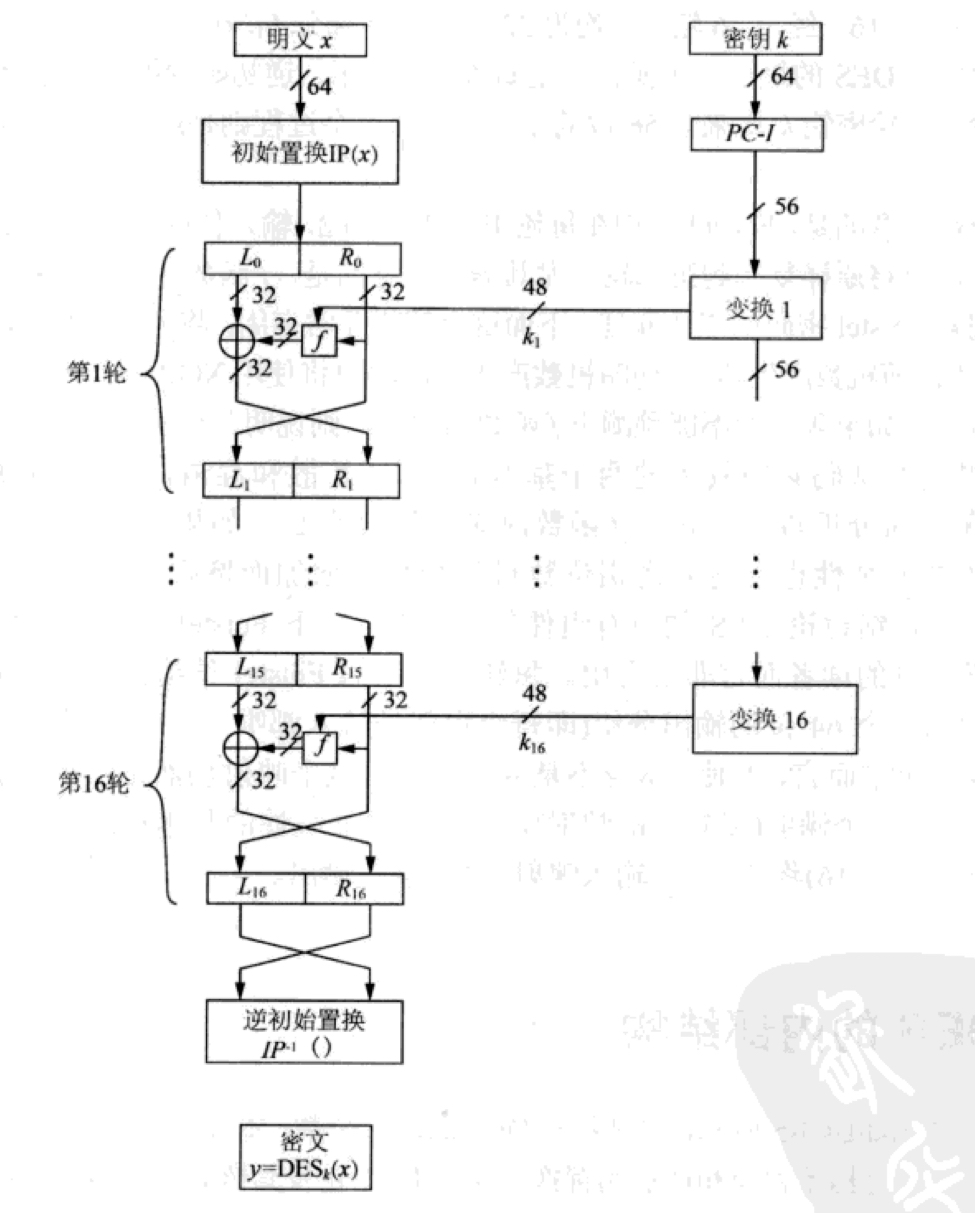
书上对Feistel网络的代数描述:每轮使用的Feistel结构都将一个64位的输入分组映射到一个64位的输出分组。对任意函数f而言,即使f本身不是双向映射的这个映射仍是双向映射。在DES中f函数实际是一个满射,使用了非线性的基本构造分组,并使用48位的轮密码ki(1≤i≤16)将32位的输入映射到32位输出上
这里我把之前的一道赛题放上,那题直接把DES的所有步骤都写全了,便于我们接下来的分析
import base64
import random
flag = "flag{************************************}"
hexadecimalcontrast = {
'0': '0000',
'1': '0001',
'2': '0010',
'3': '0011',
'4': '0100',
'5': '0101',
'6': '0110',
'7': '0111',
'8': '1000',
'9': '1001',
'a': '1010',
'b': '1011',
'c': '1100',
'd': '1101',
'e': '1110',
'f': '1111',
}
IP = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7]
IP_1 = [40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
E = [32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1]
S = [[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9, ],
[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12, ],
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13, ],
[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14, ],
[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3, ],
[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13, ],
[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12, ],
[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11, ]]
PC_1 = [57, 49, 41, 33, 25, 17, 9, 1,
58, 50, 42, 34, 26, 18, 10, 2,
59, 51, 43, 35, 27, 19, 11, 3,
60, 52, 44, 36, 63, 55, 47, 39,
31, 23, 15, 7, 62, 54, 46, 38,
30, 22, 14, 6, 61, 53, 45, 37,
29, 21, 13, 5, 28, 20, 12, 4, ]
PC_2 = [14, 17, 11, 24, 1, 5, 3, 28,
15, 6, 21, 10, 23, 19, 12, 4,
26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40,
51, 45, 33, 48, 44, 49, 39, 56,
34, 53, 46, 42, 50, 36, 29, 32, ]
P = [16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25, ]
movnum = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
def HexToBin(string):
"Convert sixteen to binary"
Binstring = ""
string = string.lower()
for i in string:
try:
Binstring += hexadecimalcontrast[i]
except:
return -1
return Binstring
def BinToStr(strbin):
"Turn the binary string to a ASCII string"
strten = ""
for i in range(len(strbin) // 8):
num = 0
test = strbin[i * 8:i * 8 + 8]
for j in range(8):
num += int(test[j]) * (2**(7 - j))
strten += chr(num)
return strten
def StrToHex(string):
"Converts a string to HEX"
hexStr = ''
for i in string:
tmp = str(hex(ord(i)))
if len(tmp) == 3:
hexStr += tmp.replace('0x', '0')
else:
hexStr += tmp.replace('0x', '')
return hexStr
def Binxor(string1, string2):
"If the length is different, only the short one is returned."
strlen = 0
xorstr = ""
if len(string1) > len(string2):
strlen = len(string2)
else:
strlen = len(string1)
for i in range(strlen):
if string1[i] == string2[i]:
xorstr += '0'
else:
xorstr += '1'
return xorstr
def SubstitutionBox(keyfield, sub):
newkeyfield = ''
for i in range(len(sub)):
newkeyfield += keyfield[sub[i] - 1]
return newkeyfield
def SubkeyGeneration(freq, C, D):
for i in range(movnum[freq]):
C = C[1:] + C[:1]
D = D[1:] + D[:1]
return C, D, SubstitutionBox(C + D, PC_2)
def enkey(secretkey):
netss = SubstitutionBox(HexToBin(StrToHex(secretkey)), PC_1)
C, D = netss[:28], netss[28:]
key = []
for i in range(16):
C, D, keyone = SubkeyGeneration(i, C, D)
key.append(keyone)
return key
def Sbox(plaintext, sub):
return HexToBin("%x" % S[sub][int(plaintext[:1] + plaintext[-1:], 2) * 16 + int(plaintext[1:-1], 2)])
def Function(plaintext, secretkey):
plaintext = Binxor(SubstitutionBox(plaintext, E),
secretkey)
sout = ''
for i in range(8):
sout += Sbox(plaintext[i * 6:(i + 1) * 6], i)
sout = SubstitutionBox(sout, P)
return sout
def endecrypt(plaintext, secretkey):
netss = SubstitutionBox(HexToBin(StrToHex(plaintext)), IP)
L, R = netss[:32], netss[32:]
for i in range(16):
L, R = R, Binxor(L, Function(R, secretkey[i]))
return SubstitutionBox(R + L, IP_1)
def encryption(plaintext, secretkey):
plaintext = plaintext + (8 - len(plaintext) % 8) * '\0'
keys = enkey(secretkey[:8])
ciphertext = ''
for i in range(len(plaintext) / 8):
ciphertext += endecrypt(plaintext[i * 8:(i + 1) * 8], keys)
return base64.b64encode(BinToStr(ciphertext))
def generate():
fw = open("random", "w")
for i in range(700):
fw.write(str(random.getrandbits(32))+"\n")
fw.close()
generate()
f = open("flag.txt", "w")
key = str(random.getrandbits(32))
ciphertext = encryption(flag, key)
f.write(ciphertext)
f.close()
Part1:IP置换
按照一定规则,将原来的64位二进制位重新排序
即上述代码中的IP与IP_1,分别为IP和IP逆置换的表
一开始觉得这两个表不应该一样才对嘛?实际上并不是,很容易想到问题在哪
下面这个图能帮助我们更好理解
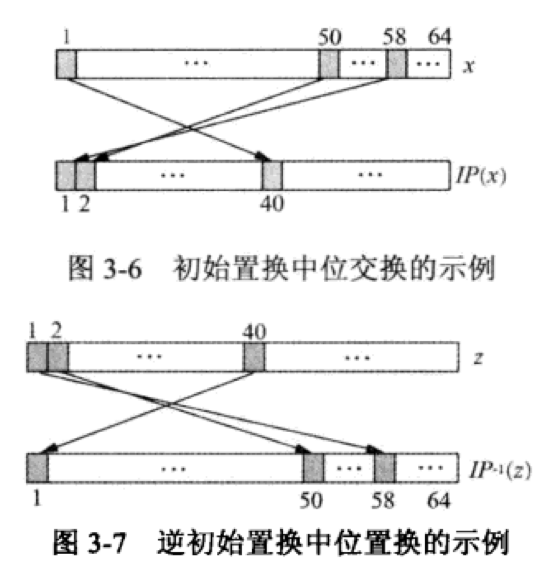
IP置换并不会增加加密的安全性,好像是为了适应当时寄存器大小而设计
Part2:f函数
step1:E扩展置换
为了适应异或密钥的48bits需要将每个32bits的部分扩充为48bits参与异或
即代码的E部分
效果如图

随后与密钥进行异或
step2:S盒压缩
根据异或所得的48bits数据,采用6进4出的8个S盒进行压缩
选取每个6bits数据的首尾组成的二进制数为行数,中间4bits所组成的二进制数为列数进行查表
代码所示的S盒的顺序好像有点问题,当时采用Crypto库里的DES解密没解出明文或许也是这个原因
需要注意的是S盒是DES中唯一一个非线性元素,人们通常通过精心设计S盒来抵御各种高级的数学攻击,如差分密码分析等
step3:P盒置换
与IP置换一样,查表即可
Part3:密钥编排
step1
PC-1表置换(同时除去8,16,···,64位(8个校验位))
step2
将剩余的56bits分为两部分,分别进行循环移位

step3
移位后将两部分合并,进行PC-2表置换,最终得到48bits的密钥
总流程如下
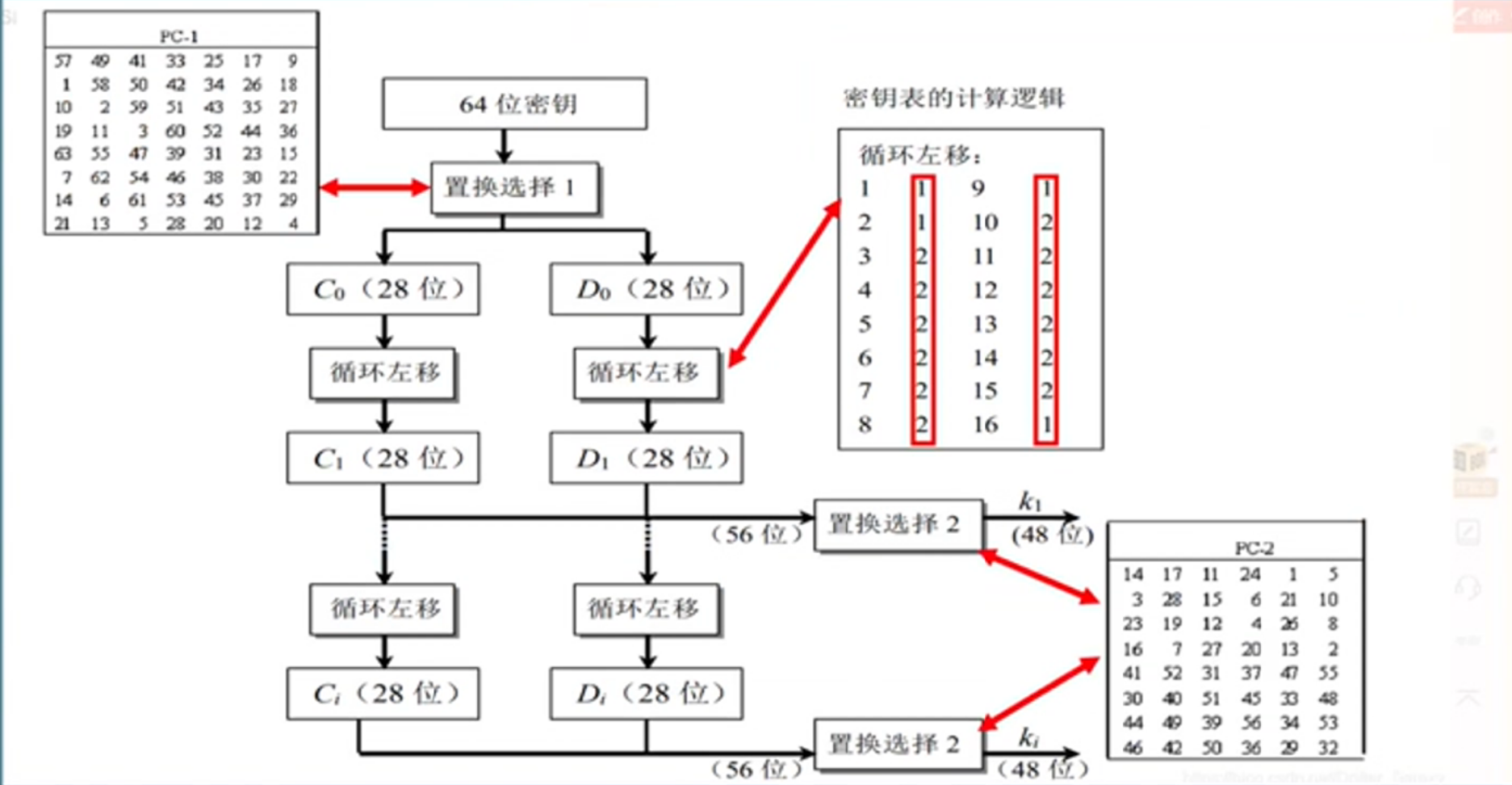
总的来说DES的确是个很精彩的算法,但是由于密钥空间较小容易受到攻击,故单重DES只用于短期安全性或加密数据价值较低的情况,但DES的变体如3DES仍然十分安全
在DES产生的几十年时间内产生了针对DES的DC及LC攻击,但是由于这两种分析攻击所需的明密文对的量并不现实,故我们认为DC和LC在现实系统中无法破解DES


