AES Learning
嗯,我相信AES(Advanced Encryption Standard)的内部结构一定很美妙,试图理解和实现一下
学长说要用c++实现,离开了python打包好的模块真的好难呀😢(慢慢补吧)
总流程如下
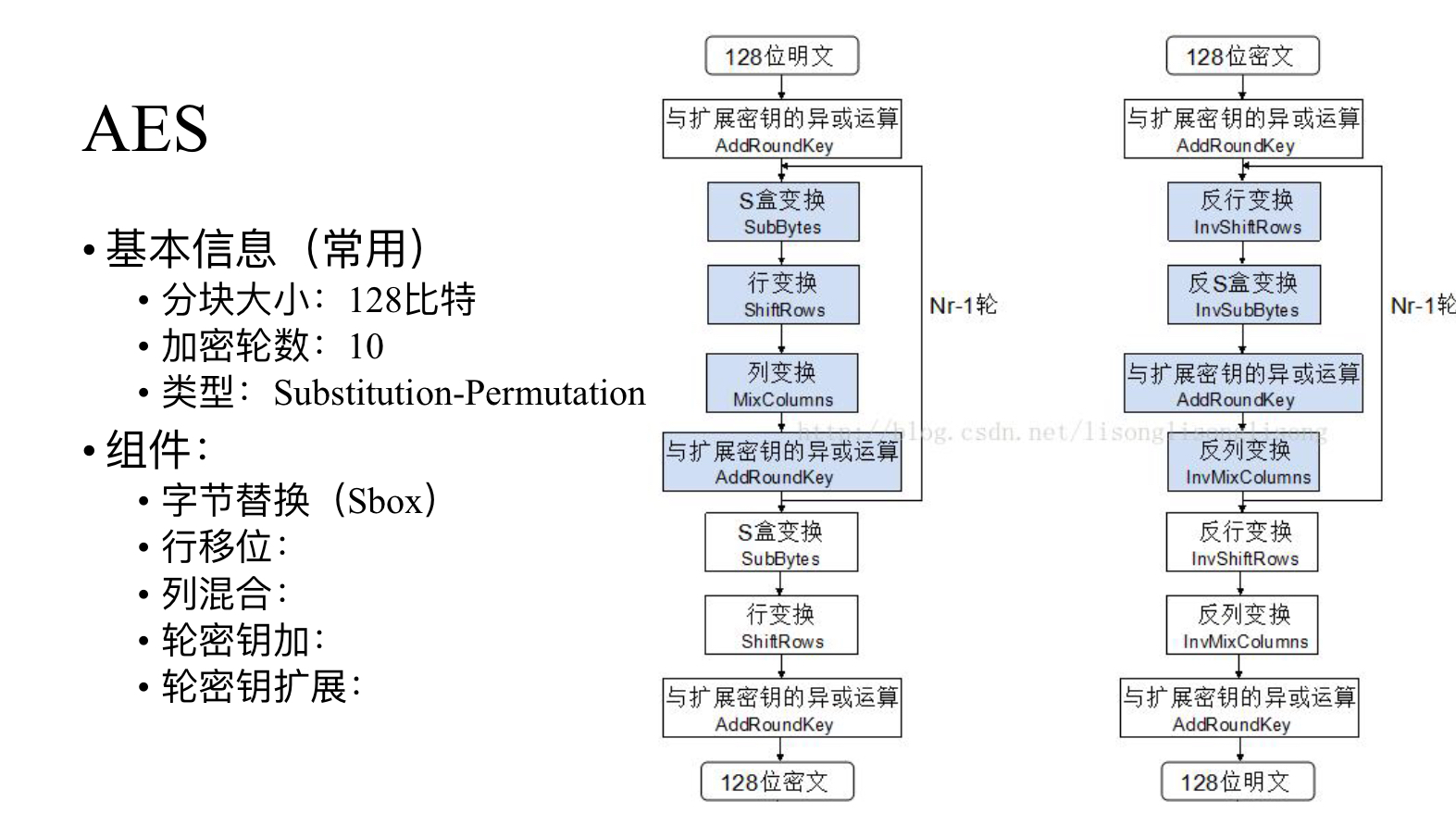
Step1:SubBytes
就是实现S盒的功能,我感觉是这几步里原理最复杂的了
AES的S盒是有一个置换表可以查,因为他的S盒是固定的
我们这里介绍一下S盒的数学描述:
首先块加密一组信息是16个字节,构成一个4×4的状态矩阵
1.对于每一个字节写出他的八位二进制下的表示
2.在GF(\(2^8\))下求逆
3.通过一个GF(\(2^8\))下的矩阵运算
先解释在GF(\(2^8\))下的求逆过程
GF(\(2^8\))为拓展域,在拓展域的表示是系数为GF(2)下的多项式,AES在GF(\(2^8\))下选取的不可约多项式为\(x^8+x^4+x^3+x+1\)(地位相当于素域上的模数)
于是\(f^-1\)满足\(f×f^-1≡1 mod(x^8+x^4+x^3+x+1)\)
即加减和乘除都是在模\(x^8+x^4+x^3+x+1\)下进行的
信息\((a_7,···,a_0)\)进入S盒,写成\(a_7x^7+···+a_0\)的形式求出逆元\((a_7',···,a_0')\)
进行矩阵运算
\(\left[\begin{matrix}b_0\\b_1\\·\\·\\·\\b_7\end{matrix}\right]=\left[\begin{matrix}1&0&0&0&1&1&1&1\\1&1&0&0&0&1&1&1\\1&1&1&0&0&0&1&1\\1&1&1&1&0&0&0&1\\1&1&1&1&1&0&0&0\\0&1&1&1&1&1&0&0\\0&0&1&1&1&1&1&0\\0&0&0&1&1&1&1&1\end{matrix}\right]\left[\begin{matrix}a'_0\\a'_1\\·\\·\\·\\a'_7\end{matrix}\right]+\left[\begin{matrix}1\\1\\0\\0\\0\\1\\1\\0\end{matrix}\right]\)mod(2)
c++实现
SBox[16][16] = {
{0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76},
{0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0},
{0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15},
{0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75},
{0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84},
{0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF},
{0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8},
{0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2},
{0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73},
{0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB},
{0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79},
{0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08},
{0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A},
{0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E},
{0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF},
{0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16}
};
Step2:ShiftRows
将状态矩阵的每一行,分别向左进行0,1,2,3个位置的循环移位
Step3:MixColums
讲状态矩阵左乘(伽罗瓦域下)一个4×4的矩阵
每一列满足
\(\left[\begin{matrix}S'_{1i}\\S'_{2i}\\S'_{3i}\\S'_{4i}\end{matrix}\right]=\left[\begin{matrix}02&03&01&01\\01&02&03&01\\01&01&02&03\\03&01&01&02\end{matrix}\right]\left[\begin{matrix}S_{1i}\\S_{2i}\\S_{3i}\\S_{4i}\end{matrix}\right]\)
Step4:AddRoundKey
轮密钥加的过程就是每一个状态矩阵与密钥扩展下的4个列进行异或,下面主要讲一下密钥扩展的过程
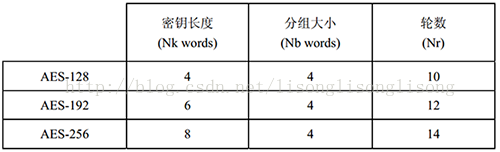
一般情况下AES是采用128bits的加密长度,但是当初Joan Daemen和Vincent Rijmen设计的时候是能够支持128,192,及256bits的加密(不同的加密长度对应的密钥长度以及轮数均不相同)
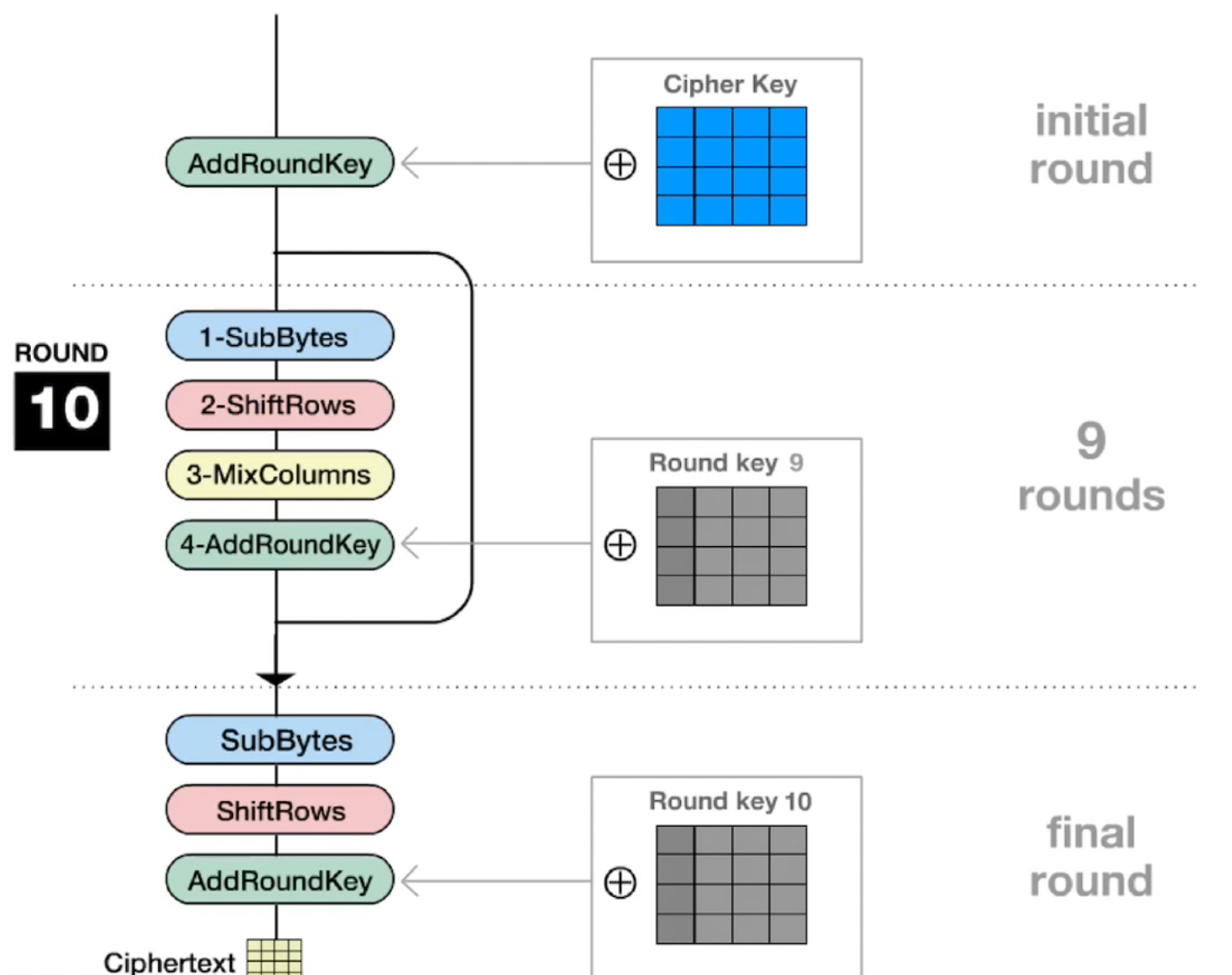
以128bits为例,我们需要将原来4字节的Cipher Key扩展成44字
第一个原始密钥用于初始变换,后面10个4×4的密钥矩阵分别用于轮密钥加的过程
在密钥扩展中从第一列开始从0开始标
满足如下递推
4\(\nmid\)i时:W[i]=W[i-4]+W[i-1]
4|i时:W[i]=W[i-4]+T(W[i-1])
T函数包括三部分:1.字循环,2.字节代换,3.轮常量异或
轮常量的构成如下图
Rcon[i]=(RC[i],0,0,0),其中RC[1]=1,RC[i]=2×RC[i-1]

注意128bits的加密前九轮所有步骤均执行,第十轮不执行列混合


