Lattice Learning1

Lattice Learning

也学了几个月的crypto了，收获不小，但是对于很多的概念并不是很清楚，虽然有关格的内容之前也有遇到过，但是都只停留在会使用别人写好的代码层面上，趁寒假还有时间把这一块内容补补

概念

格是几何空间中按照一定规则排列的无穷点的集合

定义1:设\(b_1，b_2，···，b_m\)是中m个线性无关的n维向量(n≥m)，我们取\(c_i\)∈Z，则称以\(c_i\)为组合系数的\(b_i\)的线性组合所构成的集合称为n维格，即:

\(A=L(b_1,b_2,···,b_m)\)={\(y|y=∑c_ib_i , c_i∈Z\)}

其中\(B=(b_1,b_2,···,b_m)∈Z^{n×m}\)称为格A的一个基，m称为格A的秩，n称为格A的维数。特别的当n=m时，称A为n维满秩格

格A的行列式可表示为det(A)，它是n维空间中由格A的基向量所生成的平行多面体P的体积。

对于n维满秩格，有\(det(A)=\sqrt{det(B^TB)}\)

定义2:给定基为B的格A，则由与格A中向量内积均为整数的向量所构成的集合称为A的对偶格\(A^*\)，即:

\(A^*\)={\(x∈R^n| ∀y∈A, <x,y>∈Z\)}

困难问题

主要有两个类，SVP及CVP

SVP:寻找格L中最短的非零向量

即找到\(v^*∈L,对∀v∈L,都有||v^*||≤||v||\)

CVP:对于一个非格L的向量Ω,在格中找向量v使得||Ω-v||最小

还有一系列的基于这两个问题的近似问题

其中SVP及CVP问题被证明是NP-hard问题

---

示例

emm，说了这么多还是比较抽象的

上图:

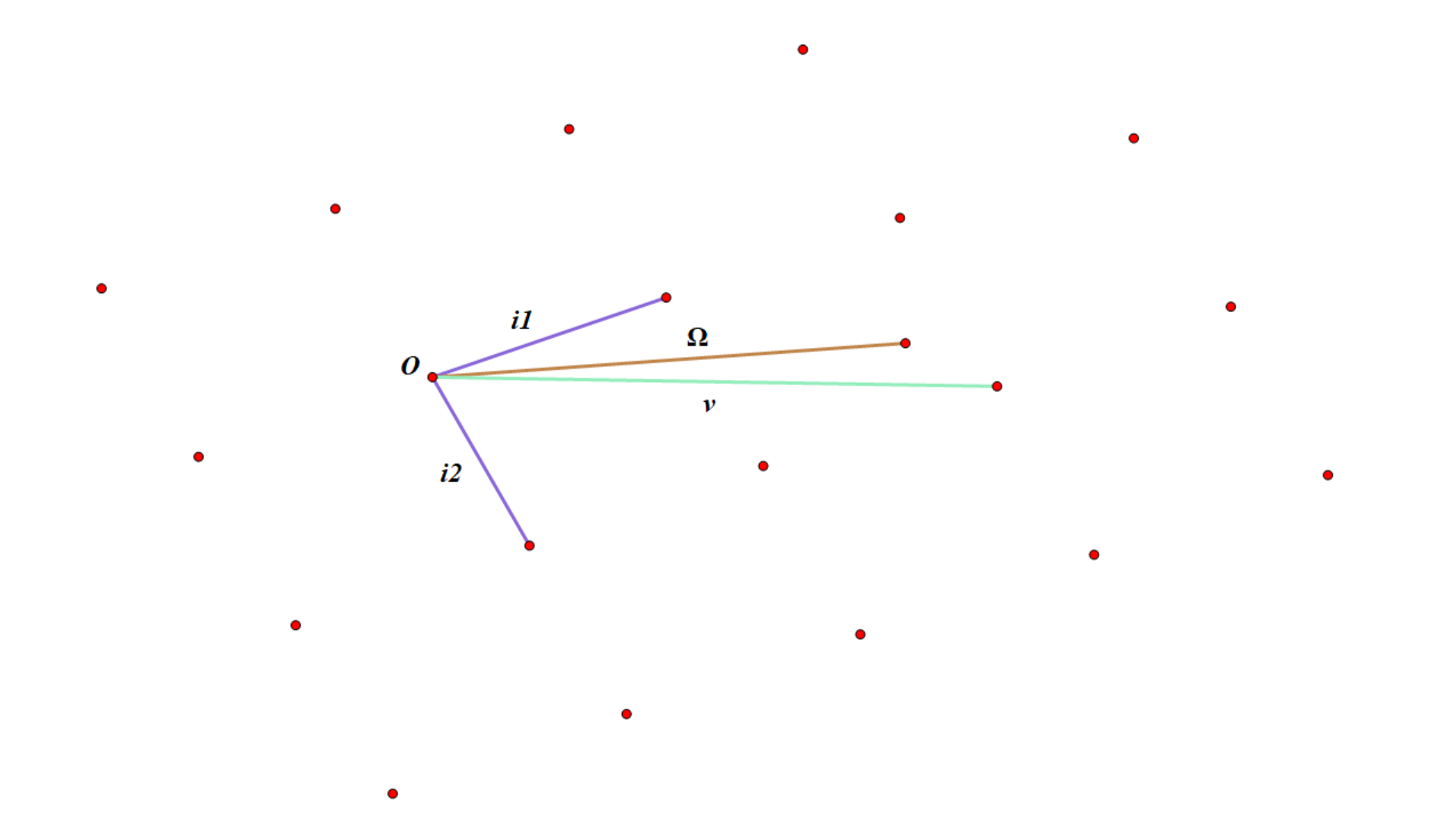
很明显，在这里的一组基是\(<i_1,i_2>\)最短向量是\(i_2\)，Ω的最近向量是v

最后我们自己随便造一个格子感受一下

条件:\(k(q+r)+s =2^{1024}p\)

\[[s,p]=[-(q+r),p]× \left[ \begin{matrix} k & 0\\ 2^{1024}& 1 \\ \end{matrix} \right] \]

在这里我们构造了格\(\left[ \begin{matrix} k & 0\\ 2^{1024}& 1 \\ \end{matrix} \right]\)

并通过条件把[s,p]嵌入，如果[s,p]刚好是这个格的最短向量，我们就能通过LLL算法在已知k的情况下求出(s,p)

摘自:2021NCTFsign

附件:https://upyun.clq0.top/signin.py

代码如下:

import gmpy2
k=94541588860584895585135152950569493777168309607384495730944110393788712443252059813470464503558980161423182930915955597122997950103392684040352673659694990925903156093591505153081718027169554019948988048641061593654540898258994671824807628660558123733006209479395447337793897155523508261277918178756662618785
n=780382574657056148524126341547161694121139907409040429176771134165303790043856598163799273195157260505524054034596118923390755532760928964966379457317135940979046201401066257918457068510403020146410174895470232276387032511651496790519359024937958635283547294676457588680828221680705802054780628993173199987362419589945445821005688218540209709368995166794607635504501281131700210990592718388166388793182269128127850804650083811982799377308916540691843310867205397
c=601133470721804838247833449664753362221136965650852411177773274117379671405966812018926891137093789704412080113310175506684194683631033003847585245560967863306852502110832136044837625931830243428075035781445021691969145959052459661597331192880689893369292311652372449853270889898705765869674961705116875378568712306021536838123003111819172078652012105725060809972222290408551883774305223612755026614701916201374200602892717051698568751566665976546137674450533774
e=65537
A=Matrix([[k,0],[2**1024,1]])
s,p=A.LLL()[0]
t1=(2**1024*p-s)//k
t2=n//p
t3=isqrt(t1^2-4*t2)
q=(t1+t3)//2
r=(t1-t3)//2
phi=(p-1)*(q-1)*(r-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
print(m)