2022-2023 春学期 矩阵与数值分析 C3 矩阵分析基础

2022-2023 春学期 矩阵与数值分析 C3 矩阵分析基础

原文

引言

本文内容来自于对矩阵与数值分析课程资料的整理；

本文所涉及的课程指东北某沿海高校，计算机学院硕士生必修课“矩阵与数值分析”，课程资料包括课程PPT、教材《计算机科学计算 第二版》[1]，以及网络资料，师兄的笔记等。

C3 矩阵分析基础

3.1 矩阵序列与级数

矩阵序列相关定义与特性

矩阵序列：按整数 k 的序列，将 \(C^{m\times n}\) 中的矩阵排成一列 \(A_1,A_2,A_3,\cdots,A_k,\cdots\)，称这列有序的矩阵为矩阵为矩阵序列，称 \(A_k\) 为矩阵序列的一般项。

矩阵序列的发散与收敛：\(\{A_k\}^\infty_{k=1}\) 为 \(C^{m\times n}\) 中的矩阵序列，其中 \(A_k=(a_{ij}^{(k)})\)，又 \(A=a_{ij}\in C^{m\times n}\)，如果 \(\lim\limits_{k\rightarrow\infty}a^{(k)}_{ij}=a_{ij}\)，对 \(i=1,2,\cdots,m;j=1,2,\cdots,n\) 均成立，则称矩阵序列 \(\{A_k\}^\infty_{k=1}\) 收敛，而 A 称为矩阵序列 \(\{A_k\}^\infty_{k=1}\) 的极限，记为 \(\lim\limits_{k\rightarrow\infty}A_k=A\)；不收敛的矩阵序列称为发散的。

可见矩阵序列收敛和矩阵中的元素都收敛的是相互充要的。

矩阵序列收敛性与范数：设 \(\{A_k\}^\infty_{k=1}\) 为 \(C^{m\times n}\) 中的矩阵序列，\(||\cdot||\) 为 \(C ^{m\times n}\) 中的一种矩阵范数，则矩阵序列 \(\{A_k\}^\infty_{k=1}\) 收敛于 A 的充要条件是 \(||A_k-A||\) 收敛于零。

相关结论：设 \(\{A_k\}^\infty_{k=1},A\in C ^{m\times n}\) ，并且 \(\lim\limits_{k\rightarrow\infty}A_k=A\)，则 \(\lim\limits_{k\rightarrow\infty}||A_k||=||A||\)；此结论只是充分条件，反过来不一定成立。

对于矩阵序列的四则运算，有：

设 \(\{A_k\}^\infty_{k=1}\), 和 \(\{B_k\}^\infty_{k=1}\)，分别为$ C ^{m\times n}$ 和 $ C ^{n\times l}$，并且 \(\lim\limits_{k\rightarrow\infty}A_k=A,\lim\limits_{k\rightarrow\infty}B_k=B\)，则

  • \(\lim\limits_{k\rightarrow\infty}(\alpha A_k+\beta B_k)=\alpha A+\beta B,\forall\alpha,\beta\in C\)
  • \(\lim\limits_{k\rightarrow\infty}A_kB_k=AB\)
  • 设 \(\{A_k\}^\infty_{k=1},A\in C ^{n\times n}\) 中的矩阵序列，并且 \(\lim\limits_{k\rightarrow\infty}A_k=A,A_k(k=1,2,\cdots)\)，和 \(A\in C ^{n\times n}\) 均为可逆矩阵，则 \(\lim\limits_{k\rightarrow\infty}A^{-1}=A^{-1}\)；注意矩阵序列可逆不能保证极限一定可逆
  • 可逆矩阵极限可能奇异，非零矩阵极限可能为零

收敛矩阵：\(A\in C^{n\times n},\lim\limits_{k\rightarrow\infty}A^k=0\)

定理：\(\rho(A)<1\) 的充要条件是：存在 \(C^{n\times n}\) 上的某种范数 \(||\cdot||\) ，使得 \(||A||<1\)

定理：设 \(C^{n\times n}\)，\(\lim\limits_{k\rightarrow\infty}A^k=0\) 的充分必要条件是存在 \(C^{n\times n}\) 上的某种范数 \(||\cdot||\) ，使得 \(||A||<1\)

所以有：

\(\rho(A)<1\Leftrightarrow\lim\limits_{k\rightarrow\infty}A^k=0\Leftrightarrow任意 \ ||A||<1\)

判断一个矩阵是否为收敛矩阵：

  • 若 \(A^k\) 容易计算，则利用其判断收敛性
  • 判断矩阵的某种范数是否小于 1
  • 计算矩阵的谱半径
例题

image-20230518201307908

image-20230518201334394

image-20230518201354238

image-20230518201420008

image-20230518201451473

矩阵级数相关定义与结论

定义：设 \(\{A_k\}^\infty_{k=1}\) 为 \(C ^{m\times n}\) 中的矩阵序列，称

\[A_1+A_2+\cdots+A_k+\cdots \]

为由矩阵序列 \(\{A_k\}^\infty_{k=1}\) 构成的矩阵级数，记为 \(\sum\limits^\infty_{k=1}A_k\)

定义：记 \(S_k=\sum\limits^k_{i=1}A_i\)，称之为矩阵级数 \(\sum\limits^\infty_{k=1}A_k\) 的前 k 项部分和，若矩阵序列 \(\{S_k\}^\infty_{k=1}\) 收敛且 \(\lim\limits_{k\rightarrow\infty}S_k=S\)，则称矩阵级数 \(\sum\limits^\infty_{k=1}A_k\) 收敛；矩阵 S 称为矩阵级数的和函数，记为 \(S=\sum\limits^\infty_{k=1}A_k\)。不收敛的矩阵级数称为发散的。矩阵级数收敛即 \(m\times n\) 个数项级数 \(\sum\limits^\infty_{k=1}a_{ij}^{(k)}\) 均收敛。

定理：设 A 为 n 阶方阵，则 \(\sum\limits_{k=0}^\infty A^k=I+A+A^2+\cdots+A^k+\cdots\) 收敛（\(A^0=I\)）的充要条件是 \(\rho(A)<1\)

定理：设 A 为 n 阶方阵，当 \(\sum\limits_{k=0}^\infty A^k\) 收敛时，有 \(\sum\limits_{k=0}^\infty A^k=(I-A)^{-1}\)，而且存在 \(C^{n\times n}\) 上的算子范数 \(||\cdot||\)，使得 \(||(I-A)^{-1}-\sum\limits^m_{k=0}A^k||\leq\frac{||A||^{m+1}}{1-||A||}\)

例题

image-20230519185032341

image-20230519190036391

image-20230519190119894

image-20230519190143789

矩阵级数绝对收敛相关结论

定义：设 \(\sum\limits_{k=1}^\infty A_k\) 为 \(C^{m\times n}\) 中的矩阵级数，其中 \(A_k=(a^{(k)}_{ij})\)。如果\(\sum\limits_{k=1}^\infty a_{ij}^{(k)}\) 对任意的 \(1\leq i\leq m,\, 1\leq j\leq n\) 均为绝对收敛的，则称矩阵级数 \(\sum\limits_{k=1}^\infty A_k\) 绝对收敛。

定理：矩阵级数 \(\sum\limits_{k=1}^\infty A_k\) 为绝对收敛的充要条件是正项级数 \(\sum\limits_{k=1}^\infty ||A_k||\)收敛

定理：若矩阵级数 \(\sum\limits_{k=1}^\infty A_k\) 是绝对收敛的，则它一定是收敛的，并且任意调换各项的顺序所得到的级数还是收敛的，且级数和不变；显然，收敛的级数不一定绝对收敛，而绝对收敛的级数一定是收敛的。

定理：设 \(\sum\limits_{k=1}^\infty A_k\) 为 \(C^{m\times n}\) 中的绝对收敛的矩阵级数，\(A=\sum\limits_{k=1}^\infty A_k\)，设 \(\sum\limits_{k=1}^\infty B_k\) 为 \(C^{n\times l}\) 中的绝对收敛的矩阵级数，\(B=\sum\limits_{k=1}^\infty B_k\)，则 \(\sum\limits_{k=1}^\infty A_k\cdot\sum\limits_{k=1}^\infty B_k\) 按任何方式排列得到的级数绝对收敛，且和为 AB。

定理，设 \(P\in C^{p\times m}\) 和 \(Q\in C^{n\times q}\) 为给定矩阵，则 \(\sum\limits_{k=0}^\infty A_k\) 收敛可以得到 \(\sum\limits_{k=0}^\infty PA_kQ\) 收敛； \(\sum\limits_{k=0}^\infty A_k\) 绝对收敛可以得到 \(\sum\limits_{k=0}^\infty PA_kQ\) 绝对收敛；且有等式 \(P(\sum\limits_{k=0}^\infty A_k)Q\)

3.2 幂级数

收敛与发散

矩阵幂级数的一般形式：\(\sum\limits_{k=0}^\infty a_kA^k\)

定理：设 \(\sum\limits^\infty_{k=0}a_kt^k\) 为收敛半径为 r 的幂级数，A 为 n 阶方阵，则

  • \(\rho(A)<r\) 时，矩阵幂级数 \(\sum\limits_{k=0}^\infty a_kA^k\) 绝对收敛
  • \(\rho(A)>r\) 时，矩阵幂级数 \(\sum\limits_{k=0}^\infty a_kA^k\) 发散

定理：设 \(\sum\limits_{k=0}^\infty a_k(z-z_0)^k\) 为收敛半径为 r 的幂级数，A 为 n 阶方阵，

  • 如果 A 的特征值均落在收敛圆内，即 \(|\lambda-z_0|<r\)，其中 \(\lambda\) 为任意特征值，则矩阵幂级数 \(\sum\limits_{k=0}^\infty a_k(A-z_0I)^k\) 绝对收敛
  • 若有某个 \(\lambda_{i_0}\) 使得 \(|\lambda_{i_0}-z_0|>r\)，则幂级数 \(\sum\limits_{k=0}^\infty a_k(A-z_0I)^k\) 发散

幂级数与解析函数的关系

image-20230519192403417

image-20230519192415341

利用 Jordan 分解计算矩阵函数

image-20230519193102336

image-20230519193110897

定理：设 \(f(z)=\sum\limits^\infty_{k=0}a_kz^k\) 是收敛半径为 r 的幂级数，J 是特征值为 \(\lambda\) 的 n 阶 Jordan 块阵，且 \(|\lambda|<r\)，则

\[f(J)= \begin{pmatrix} f(\lambda)&f'(\lambda)&\cdots&\frac{f^{(n-1)}(\lambda)}{(n-1)!}\\ &f(\lambda)&\ddots&\vdots\\ &&\ddots&f'(\lambda)\\ &&&f(\lambda) \end{pmatrix} \]

定理：设 \(f(z)=\sum\limits^\infty_{k=0}a_k(z-z_0)^k\) 是收敛半径为 r 的幂级数，J 是特征值为 \(\lambda\) 的 n 阶 Jordan 块阵，且 \(|\lambda-z_0|<r\)，则

\[f(J)= \begin{pmatrix} f(\lambda)&f'(\lambda)&\cdots&\frac{f^{(n-1)}(\lambda)}{(n-1)!}\\ &f(\lambda)&\ddots&\vdots\\ &&\ddots&f'(\lambda)\\ &&&f(\lambda) \end{pmatrix} \]

定理：设 \(f(z)=\sum\limits^\infty_{k=0}a_kz^k\) 是收敛半径为 r 的幂级数，J 是特征值为 \(\lambda\) 的 n 阶 Jordan 块阵，且 \(|t\lambda|<r\)，则

\[f(tJ)= \begin{pmatrix} f(t\lambda)&tf'(\lambda)&\cdots&\frac{t^{(n-1)}f^{(n-1)}(t\lambda)}{(n-1)!}\\ &f(t\lambda)&\ddots&\vdots\\ &&\ddots&tf'(\lambda)\\ &&&f(t\lambda) \end{pmatrix} \]

定理（利用矩阵的 Jordan 分解求矩阵函数 f(A) 的具体表达式）：设 \(f(z)=\sum\limits^\infty_{k=0}a_k(z-z_0)^k\) 为收敛半径为 r 的幂级数，A 为 n 阶方阵，\(A=TJT^{-1}\) 为其 Jordan 分解， \(J=\mathrm{diag}(J_1,J_2,\cdots,J_s)\)；当 A 的特征值均落在收敛圆内时，即 \(|\lambda-z_0|<r\)，其中 \(\lambda\) 为 A 的任意特征值，则矩阵幂级数 \(\sum\limits^\infty_{k=0}a_k(z-z_0)^k\) 绝对收敛，并且和矩阵为:

\[f(A)=T\mathrm{diag}(f(J_1),f(J_2),\cdots,f(J_s))T^{-1} \]

其中 \(f(J_i)\) 的定义如前表达式。

注意，若 A 的特征值为 \(\lambda_1,\lambda_2,\cdots,\lambda_n\)，则 f(A) 的特征值应为 \(f(\lambda_1),f(\lambda_2),\cdots,f(\lambda_n)\)

计算矩阵函数值的基本步骤：

  1. 计算 Jordan 分解 \(A=TJT^{-1}=T\mathrm{diag}(J_1,\cdots,J_s)T^{-1}\)
  2. 求 \(f(A)=T\mathrm{diag}(f(J_1),\cdots,f(J_s))T^{-1}\)
例题

image-20230520141258088

已知 \(J_i=\begin{pmatrix}-1&1&&\\ &-1&1\\&&-1&1\\&&&-1\end{pmatrix}\)，求 \(e^{J_i},\;e^{tJ_i}\)

解：

\[e^{J_i}= \begin{pmatrix} e^{-1}&e^{-1}&\frac{e^{-1}}{2}&\frac{e^{-1}}{6}\\ &e^{-1}&e^{-1}&\frac{e^{-1}}{2}\\ &&e^{-1}&e^{-1}\\ &&&e^{-1} \end{pmatrix}\\ e^{tJ_i}= \begin{pmatrix} e^{-t}&te^{-t}&\frac{t^2e^{-t}}{2}&\frac{t^3e^{-t}}{6}\\ &e^{-t}&te^{-t}&\frac{t^2e^{-t}}{2}\\ &&e^{-t}&te^{-t}\\ &&&e^{-t} \end{pmatrix} \]

image-20230520142211513

求 sinA，sinAt，其中

\[A= \begin{pmatrix} 1&&&\\ &2&&\\ &&3&\\ &&&4\\ \end{pmatrix},\; \sin A= \begin{pmatrix} \sin1&&&\\ &\sin2&&\\ &&\sin3&\\ &&&\sin4\\ \end{pmatrix},\; \sin At= \begin{pmatrix} \sin t&&&\\ &\sin2t&&\\ &&\sin3t&\\ &&&\sin4t\\ \end{pmatrix};\\ A= \begin{pmatrix} 1&&&\\ &1&&\\ &&1&\\ &&&1\\ \end{pmatrix},\; \sin A= \begin{pmatrix} \sin1&&&\\ &\sin1&&\\ &&\sin1&\\ &&&\sin1\\ \end{pmatrix},\; \sin At= \begin{pmatrix} \sin t&&&\\ &\sin t&&\\ &&\sin t&\\ &&&\sin t\\ \end{pmatrix};\\ A= \begin{pmatrix} 1&&&\\ &1&1&\\ &&1&1\\ &&&1\\ \end{pmatrix},\; \sin A= \begin{pmatrix} \sin1&&&\\ &\sin1&\cos1&-\frac{\sin1}{2}\\ &&\sin1&\cos1\\ &&&\sin1\\ \end{pmatrix},\; \sin At= \begin{pmatrix} \sin t&&&\\ &\sin t&t\cos t&-\frac{t^2\sin t}{2}\\ &&\sin t&t\cos t\\ &&&\sin t\\ \end{pmatrix};\\ \]

image-20230520145644818

image-20230520145653998

有限待定系数法

问题：给定函数 f(x)，计算 f(Ax)

挑战：为避免计算矩阵的 Jordan 分解

\[f(\lambda t)=p(\lambda,t)\psi(\lambda)+q(\lambda,t) \]

\(\psi(\lambda)\) 为特征多项式，\(q(\lambda,t)\) 为次数不超过 n-1 的含参多项式

\[\psi(\lambda)=\det(A-\lambda I),\\ q(\lambda,t)=b_{n-1}(t)\lambda^{n-1}+\cdots+b_1(t)\lambda+b_0(t) \]

有 Hamilton-Catley 定理可知 \(\psi(A)=0\)，从而

\[f(At)=q(A,t) \]

关键：确定含参系数 \(b_{n-1}(t),\cdots,b_1(t),b_0(t)\)

显然，A 的特征多项式

\[\psi(\lambda)=\det(A-\lambda I)=\prod\limits^s_{i=1}(\lambda-\lambda_i)^{m_i}\Rightarrow\psi^{(j)}(\lambda_i)=0,\; j=0,\cdots,m_j-1,\; i=1,\cdots,s \]

故将 \(f(\lambda t)=p(\lambda,t)\psi(\lambda)+q(\lambda,t)\) 两端对 \(\lambda\) 求导，得到

\[\begin{aligned} f(\lambda t)&=p(\lambda,t)\psi(\lambda)+q(\lambda,t)\\ &\Rightarrow \left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}f(\lambda t)\right|_{\lambda=\lambda_i}=\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}q(\lambda,t)\right|_{\lambda=\lambda_i}\\ &\Rightarrow \left . t^j\frac{\mathrm{d}^j}{\mathrm{d}u^j}f(u)\right|_{u=\lambda_it}=\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}q(\lambda,t)\right|_{\lambda=\lambda_i} \end{aligned} \]

n 个方程，n 个变量的线性方程组

待定系数法的步骤：

  1. 计算 A 的特征多项式 \(\psi(\lambda)=\det(A-\lambda I)\)

  2. 定义 \(q(\lambda,t)=b_{n-1}(t)\lambda^{n-1}+\cdots+b_1(t)\lambda+b_0(t)\)

    利用(可假设 t=1)

    \[\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}f(\lambda t)\right|_{\lambda=\lambda_i}=\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}q(\lambda,t)\right|_{\lambda=\lambda_i} \quad或\quad \left . t^j\frac{\mathrm{d}^j}{\mathrm{d}u^j}f(u)\right|_{u=\lambda_it}=\left . \frac{\mathrm{d}^j}{\mathrm{d}\lambda^j}q(\lambda,t)\right|_{\lambda=\lambda_i} \]

    确定含参系数 \(b_{n-1}(t),\cdots,b_1(t),b_0(t)\)

  3. 计算(假设 t=1，f(A)=q(A)) \(f(At)=q(A,t)\)

例题

image-20230520145819049

image-20230520145835875

矩阵函数等式

若 \(\forall A \in C^{n\times n}\)，总有：

  • \(\sin(-A)=-\sin A,\cos(-A)=\cos A\)
  • \(e^{iA}=\cos A+i\sin A,\, \cos A=\frac{1}{2}(e^{iA}+e^{-iA}),\,\sin A=\frac{1}{2i}(e^{iA}-e^{-iA})\)

若 \(A,B\in C^{n\times n}\)，且 AB=BA，则

  • \(e^Ae^B=e^Be^A=e^{A+B}\)
  • \(\sin(A+B)=\sin A\cos B+\cos A\sin B\)
  • \(\cos(A+B)=\cos A\cos B-\sin A\sin B\)

若 A=B，则 \(cos2A=\cos^2A-\sin^2A,\,\sin2A=2\sin A\cos A\)

对任何 n 阶方阵 A，\(e^A\) 总是可逆矩阵

\[e^Ae^{-A}=e^{-A}e^A=e^0=I \]

sinA 和 cosA 不一定可逆，例如：

\[A=\begin{pmatrix} \pi&0\\0&\frac{\pi}{2} \end{pmatrix} \\ \sin A=\begin{pmatrix}\sin\pi&0\\0&\sin\frac{\pi}{2}\end{pmatrix}=\begin{pmatrix}0&0\\0&1\end{pmatrix} \\\cos A=\begin{pmatrix}\cos\pi&0\\0&\cos\frac{\pi}{2}\end{pmatrix}=\begin{pmatrix}-1&0\\0&0\end{pmatrix} \]

其他若干结论：

  • \(f(A^T)=f(A)^T\)
  • \(\det(e^A)=e^{trA}\)
  • \((e^{A})^{-1}=e^{-A}\)
  • \(||e^A||\leq e^{||A||}\)
  • 若 A 为 Hermite 阵，则 \(e^{iA}\) 是酉阵
例题

image-20230520150027753

3.3 矩阵的微积分

含参矩阵微分

元素为函数的矩阵微分：如果矩阵 \(A(t)=(a_{ij}(t))_{m\times n}\) 的每一个元素 \(a_{ij}(t),i=1,2,\cdots,m;j=1,2,\cdots,n\)，在[a,b] 上均为变量 t 的可微函数，则称 A(t) 可微，且导数定义为(也就是针对每个矩阵元素对 t 求导):

\[A'(t)=\frac{d}{dt}A(t)=(\frac{d}{dt}a_{ij}(t))_{m\times n} \]

求导法则：

设 A(t), B(t) 是可进行运算的两个可微矩阵，则

  • \((A(t)+B(t))'=A'(t)+B'(t)\)
  • \((A(t)B(t))'=A'(t)B(t)+A(t)B'(t)\)
  • \((\alpha A(t))'=\alpha\cdot A'(t)\)，其中 \(\alpha\) 为任意常数
  • 当 \(A^{-1}(t)\) 为可微矩阵时，有 \((A^{-1}(t))'=-A^{-1}(t)A'(t)A^{-1}(t)\)
  • 当 \(u=f(t)\) 关于 t 可微时，有 \((A(u))'=f'(t)\frac{d}{du}A(u)\)

函数矩阵的高阶导数定义为：

\[\frac{d^k}{dt^k}(A(t))=\frac{d}{dt}(\frac{d^{k-1}}{dt^{k-1}}(A(t))) \]

注：\((A^m(t))'=mA^{m-1}(t)(A(t))'\) 不一定成立, \(A(t)(A(t))'\neq(A(t))'A(t)\), 事实上 \((A^2(t))'=(A(t)A(t))'=A'(t)A(t)+A(t)A'(t)\neq2A'(t)A(t)\)

特殊矩阵函数导数

设 n 阶方阵 A 与 t 无关，则有：

  • \((e^{tA})'=Ae^{tA}=e^{tA}A\)
  • \((\sin(tA))'=A\cdot\cos(tA)=\cos(tA)\cdot A\)
  • \((\cos(tA))'=-A\cdot\sin(tA)=-\sin(tA)\cdot A\)
重要的例题

可利用特殊点的导数值求相应矩阵

image-20230523001050871

例题

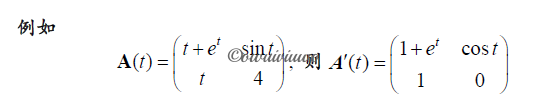
image-20230523000932923

image-20230523001011524

矩阵函数积分

如果矩阵 \(A(t)=(a_ij(t))_{m\times n}\) 的每一个元素 \(a_ij(t)\) 都是区间 \([t_0,t_1]\) 上的可积函数，则定义 A(t) 在区间 \([t_0,t_1]\) 上的积分为（对矩阵积分也就是对矩阵中每个元素积分）：

\[\int^{t_1}_{t_0}A(t)dt=(\int^{t_1}_{t_0}a_{ij}(t)dt)_{m\times n} \]

性质（与函数的积分类似）

  • \(\int^{t_1}_{t_0}(\alpha A(t)+\beta B(t))dt=\alpha\int^{t_1}_{t_0}A(t)dt+\beta\int^{t_1}_{t_0} B(t))dt,\;\forall\alpha,\beta\in C\)

  • \(\int^{t_1}_{t_0}(A(t)B)dt=\int^{t_1}_{t_0}A(t)dtB\) 其中 B 为常数矩阵

    \(\int^{t_1}_{t_0}(AB(t))dt=A\int^{t_1}_{t_0}B(t)dt\) 其中 A 为常数矩阵

  • 当 A(t) 在 [a,b] 上连续可微时，对任意 \(t\in(a,b)\) ，有 \(\frac{d}{dt}(\int^{t}_{a}A(\tau)d\tau)=A(t)\)

  • 当 A(t) 在 [a,b] 上连续可微时，对任意 \(t\in(a,b)\) ，有 \(\int^{b}_{a}\frac{dA(t)}{dt}dt=A(b)-A(a)\)

* 相对于矩阵变量的微分

应该不会考 😃

函数对矩阵求导：设 \(X=(x_{ij})_{m\times n}\)，函数 \(f(X)=f(x_{11},x_{12},\cdots,x_{1n},x_{21},\cdots,x_{mn})\) 为 mn 元的多元函数，且 \(\frac{\partial{f}}{\partial{x_{ij}}}(i=1,2,\cdots,m;j=1,2,\dots,n)\) 都存在，定义 f(X) 对矩阵 X 的导数为：

\[\frac{d}{dX}f(X)=(\frac{\partial{f}}{\partial{x_{ij}}})_{m\times n}= \begin{pmatrix} \frac{\partial{f}}{\partial{x_{ij}}}&\cdots&\frac{\partial{f}}{\partial{x_{ij}}}\\ \cdots&\ddots&\cdots\\ \frac{\partial{f}}{\partial{x_{ij}}}&\cdots&\frac{\partial{f}}{\partial{x_{ij}}} \end{pmatrix} \]

例题

image-20230523001246960

image-20230523001308189

image-20230523001322053

image-20230523001342322

image-20230523001408023

* 微分方程组相关内容

应该不会考 😃

可参考第七章的内容

一阶线性常系数齐次微分方程组

问题描述

image-20230523001446117

解的存在性

image-20230523001459677

解的唯一性

image-20230523001512861

一阶线性常系数非齐次微分方程组

问题描述

image-20230523001524648

解的存在性

image-20230523001536719

例题

image-20230523001554662

image-20230523001625341

image-20230523001639426

END

  1. 《计算机科学计算 第二版》 作者: 张宏伟 金光日 施吉林；出版社: 高等教育出版社；页数: 379；定价: 38.1元；装帧: 平装-胶订；ISBN: 9787040365955 出版年：2013；学科主题: 电子计算机 教材 科学计算-高等学校；中图法分类号: TP301.6； 一般附注: 高等学校教材 ↩︎

posted @ 2023-05-23 00:48  owuiviuwo  阅读(31)  评论(0)  编辑  收藏  举报