2022-2023 春学期 矩阵与数值分析 C2 矩阵的变换和计算
原文
引言
本文内容来自于对矩阵与数值分析课程资料的整理;
本文所涉及的课程指东北某沿海高校,计算机学院硕士生必修课“矩阵与数值分析”,课程资料包括课程PPT、教材《计算机科学计算 第二版》,以及网络资料,师兄的笔记等。
C2 矩阵的变换和计算
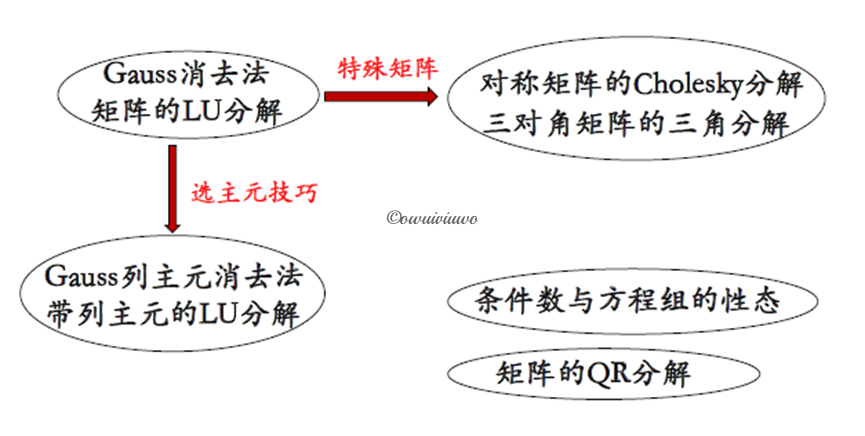
2.1 矩阵的三角分解及其应用
设法将一个一般的矩阵计算问题转化为一个或几个易于求解的矩阵计算问题——矩阵分解
Gauss 消去法与矩阵的 LU 分解
Gauss消去法
Gauss消去法的实质是首先通过一系列的初等行变换将增广矩阵 \((A|b)\) 化成上三角增广矩阵 \((U|c)\),然后通过回代求解与 \(Ax=b\) 同解的三角方程组 \(Ux=c\)。
* 例1 Gauss 消去法求解线性方程组
\[\begin{equation}
\left\{
\begin{array}{l}
2x_1&+x_2&+x_3& &= 4 &r_1^{(0)}\\
4x_1&+3x_2&+3x_3&+x_4 &= 11 &r_2^{(0)}\\
8x_1&+7x_2&+9x_3&+5x_4&=29 &r_3^{(0)}\\
6x_1&+7x_2&+9x_3&+8x_4&=30 &r_4^{(0)}
\end{array}
\right.
\end{equation}
\]
第一步,消去 \(r_2^{(0)},\ r_3^{(0)},\ r_4^{(0)}\) 中的 \(x_1\),也就是 \(r_2^{(1)}=r_2^{(0)}-2r_1^{(0)}\)、\(r_3^{(1)}=r_3^{(0)}-4r_1^{(0)}\)、\(r_4^{(1)}=r_4^{(0)}-3r_1^{(0)}\);得到
\[\begin{equation}
\left\{
\begin{array}{l}
2x_1&+x_2&+x_3&&=4 &r_1^{(0)}\\
&+x_2&+x_3&+x_4&=3 &r_2^{(1)}\\
&+3x_2&+5x_3&+5x_4&=13 &r_3^{(1)}\\
&+4x_2&+6x_3&+8x_4&=18 &r_4^{(1)}\\
\end{array}
\right.
\end{equation}
\]
第二步,消去 \(r_3^{(1)},\ r_4^{(1)}\) 中的 \(x_2\),也就是 \(r_3^{(2)}=r_3^{(1)}-3r_2^{(1)}\)、\(r_4^{(2)}=r_4^{(1)}-4r_2^{(1)}\);得到
\[\begin{equation}
\left\{
\begin{array}{l}
2x_1&+x_2&+x_3&&=4 &r_1^{(0)}\\
&+x_2&+x_3&+x_4&=3 &r_2^{(1)}\\
&&+2x_3&+2x_4&=4 &r_3^{(2)}\\
&&+2x_3&+4x_4&=6 &r_4^{(2)}\\
\end{array}
\right.
\end{equation}
\]
第三步,消去 \(r_4^{(2)}\) 中的 \(x_3\),也就是 \(r_4^{(3)}=r_4^{(2)}-r_3^{(2)}\);得到
\[\begin{equation}
\left\{
\begin{array}{l}
2x_1&+x_2&+x_3&&=4 &r_1^{(0)}\\
&+x_2&+x_3&+x_4&=3 &r_2^{(1)}\\
&&+2x_3&+2x_4&=4 &r_3^{(2)}\\
&&&+2x_4&=2 &r_4^{(3)}\\
\end{array}
\right.
\end{equation}
\]
最后,通过上一步得到的 \(x_4\) 值,逐个回代求解即可得到原方程组的解
\[\begin{equation}
\left\{
\begin{array}{l}
2x_1&+x_2&+x_3&&=4 & \Rightarrow&x_1=1\\
&+x_2&+x_3&+x_4&=3 &\Rightarrow&x_2=1\\
&&+2x_3&+2x_4&=4 &\Rightarrow&x_3=1\\
&&&+2x_4&=2 &\Rightarrow&x_4=1\\
\end{array}
\right.
\end{equation}
\]

通过例题的过程,可以进一步明确使用 Gauss 消去法求解线性方程组的过程如下:
针对线性方程组 \(Ax=b\),可以构造增广矩阵
\[\left\{
\begin{matrix}
a_{11}&a_{12}&\cdots&a_{1_n}&b_1\\
a_{21}&a_{22}&\cdots&a_{2_n}&b_2\\
\vdots& \vdots & \ddots&\vdots&\vdots\\
a_{11}&a_{12}&\cdots&a_{1_n}&b_1\\
\end{matrix}
\right\}
\]
第一步,第 i 行 - 第 1 行\(\times\frac{a_{i1}}{a_{11}},\ i=2,\cdots,n\)
\[\left\{
\begin{matrix}
a_{11}&a_{12}&\cdots&a_{1_n}&b_1\\
a_{21}&a_{22}&\cdots&a_{2_n}&b_2\\
\vdots& \vdots & \ddots&\vdots&\vdots\\
a_{11}&a_{12}&\cdots&a_{1_n}&b_1\\
\end{matrix}
\right\}
\Rightarrow
\left\{
\begin{matrix}
a_{11}&a_{12}&\cdots&a_{1_n}&b_1\\
0&a_{22}^{(1)}&\cdots&a_{2_n}^{(1)}&b_2^{(1)}\\
\vdots& \vdots & \ddots&\vdots&\vdots\\
0&a_{12}^{(1)}&\cdots&a_{1_n}^{(1)}&b_1^{(1)}\\
\end{matrix}
\right\}
\]
这一步的运算量(乘除法)为 \((n-1)*(n+1)\);
第 k 步,第 i 行 - 第 k 行\(\times\frac{a_{ik}^{(k-1)}}{a^{(k-1)}_{kk}},\ i=k+1,\cdots,n\)
\[\left\{
\begin{matrix}
a^{(0)}_{1,1}&\cdots&a^{(0)}_{1,k}&a^{(0)}_{1,k+1}&\cdots&a^{(0)}_{1,n}&b^{(0)}_{1}\\
&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots\\
&&a^{(k-1)}_{k.k}&a^{(k-1)}_{k.k+1}&\cdots&a^{(k-1)}_{k.n}&b^{(k-1)}_{k}\\
&&a^{(k-1)}_{k+1.k}&a^{(k-1)}_{k+1.k+1}&\cdots&a^{(k-1)}_{k+1.k}&b^{(k)}_{k+1}\\
&&\vdots&\vdots&\ddots&\vdots&\vdots\\
&&a^{(k-1)}_{n.k}&a^{(k-1)}_{n.k+1}&\cdots&a^{(k-1)}_{n,n}&b^{(k-1)}_{n}\\
\end{matrix}
\right\}
\Rightarrow
\left\{
\begin{matrix}
a^{(0)}_{1,1}&\cdots&a^{(0)}_{1,k}&a^{(0)}_{1,k+1}&\cdots&a^{(0)}_{1,n}&b^{(0)}_{1}\\
&\ddots&\vdots&\vdots&\ddots&\vdots&\vdots\\
&&a^{(k-1)}_{k.k}&a^{(k-1)}_{k.k+1}&\cdots&a^{(k-1)}_{k.n}&b^{(k-1)}_{k}\\
&&&a^{(k)}_{k+1.k+1}&\cdots&a^{(k)}_{k+1.n}&b^{(k)}_{k+1}\\
&&&\vdots&\ddots&\vdots&\vdots\\
&&&a^{(k)}_{n.k+1}&\cdots&a^{(k)}_{n,n}&b^{(k)}_{n}\\
\end{matrix}
\right\}
\]
这一步的运算量(乘除法)为 \((n-k)*(1+n-k+1)=(n-k)(n-k+2)\);
将系数矩阵化为上三角矩阵后,运用回代法求解:
\[\left\{
\begin{matrix}
a_{11}^{(0)}&a_{12}^{(0)}&\cdots&a_{1_n}^{(0)}\\
&a_{22}^{(1)}&\cdots&a_{2_n}^{(1)}\\
& & \ddots&\vdots\\
&&&a_{1_n}^{(1)}\\
\end{matrix}
\right\}
\left\{
\begin{matrix}
x_1\\
x_2\\
\vdots\\
\\
x_n
\end{matrix}
\right\}
=
\left\{
\begin{matrix}
b_1^{(0)}\\
b_2^{(1)}\\
\vdots\\
b_n^{(n-1)}
\end{matrix}
\right\}
\\
\]
可知 \(x_k\) 的计算过程如下所示:
\[x_k=\frac{b^{(k-1)}_{k}-a^{(k-1)}_{k,k+1}x_{k+1}-a^{(k-1)}_{kn}x_n}{a^{(k-1)}_{kk}},\ k=n,n-1,\cdots,1x_k=\frac{b^{(k-1)}_{k}-a^{(k-1)}_{k,k+1}x_{k+1}-a^{(k-1)}_{kn}x_n}{a^{(k-1)}_{kk}},\ k=n,n-1,\cdots,1
\]
第 k 步的计算量(乘除法次数)为: \(n-k+1\)
通过上述分析,可以分析针对 n 阶线性方程组,使用 Gauss 消去法的总计算量(乘除法次数)为:
\[\begin{equation}
\left\{
\begin{array}{l}
\sum\limits^{n-1}_{k=1}(n-k)(n-k+2)=\frac{1}{3}n^3+\frac{1}{2}n^2-\frac{5}{6}&(1)\\
\sum\limits^{n}_{k=1}(n-k+1)=\frac{n(n+1)}{a}&(2)\\
\end{array}
\right.
\end{equation}
\]
\[(1)+(2)=\frac{n^3}{3}+n^2-\frac{n}{3}
\]
可知,其与 \(\frac{n^3}{3}\) 是同阶的
若还考虑加减法,则与 \(\frac{2n^3}{3}\) 是同阶的。
矩阵的 LU 分解
自然的, Gauss 消去法将原方程组的系数矩阵转换成了上三角矩阵简便了计算。也存在其他转换上三角矩阵的方法;例如通过矩阵乘法的方式表示上述 Gauss 消去的过程
在 *例1中,可以将三次消元过程写成矩阵形式
\[\begin{aligned}
L_1A&=
\left\{
\begin{matrix}
1&&&\\
-2&1&&\\
-4&&1&\\
-3&&&1
\end{matrix}
\right\}
\left\{
\begin{matrix}
2&1&1&0\\
4&3&3&1\\
8&7&9&5\\
6&7&9&8
\end{matrix}
\right\}
&=
\left\{
\begin{matrix}
2&1&1&0\\
0&1&1&1\\
0&3&5&5\\
0&4&6&8
\end{matrix}
\right\}
\\
L_2(L_1A)&=
\left\{
\begin{matrix}
1&&&\\
&1&&\\
&-3&1&\\
&-4&&1
\end{matrix}
\right\}
\left\{
\begin{matrix}
2&1&1&0\\
0&1&1&1\\
0&3&5&5\\
0&4&6&8
\end{matrix}
\right\}
&=
\left\{
\begin{matrix}
2&1&1&0\\
0&1&1&1\\
0&0&2&2\\
0&0&2&4
\end{matrix}
\right\}
\\
L_3(L_2L_1A)&=
\left\{
\begin{matrix}
1&&&\\
&1&&\\
&&1&\\
&&-1&1
\end{matrix}
\right\}
\left\{
\begin{matrix}
2&1&1&0\\
0&1&1&1\\
0&0&2&2\\
0&0&2&4
\end{matrix}
\right\}
&=
\left\{
\begin{matrix}
2&1&1&0\\
0&1&1&1\\
0&0&2&2\\
0&0&0&2
\end{matrix}
\right\}&=U
\end{aligned}
\]
接下来,对矩阵 \(L_1,\ L_2,\ L_3\)分别求逆,可得
\[L_1^{-1}=
\left\{
\begin{matrix}
1&&&\\
2&1&&\\
4&&1&\\
3&&&1
\end{matrix}
\right\}
\\
L_2^{-1}=
\left\{
\begin{matrix}
1&&&\\
&1&&\\
&3&1&\\
&4&&1
\end{matrix}
\right\}
\\
L_3^{-1}=
\left\{
\begin{matrix}
1&&&\\
&1&&\\
&&1&\\
&&1&1
\end{matrix}
\right\}
\]
且易得
\[L_1^{-1}L_2^{-1}=
\left\{
\begin{matrix}
1&&&\\
2&1&&\\
4&3&1&\\
3&4&&1
\end{matrix}
\right\}
\]
令 \(L=L_1^{-1}L_2^{-1}L_3^{-1}\),从而有 \(L^{-1}=L_3L_2L_2\),而 \(L^{-1}A=U\),也就可以得到 \(A=LU\);
定义:对于 \(n\) 阶方阵 \(A\) ,如果存在 \(n\) 阶单位下三角矩阵 \(L\)(为下三角矩阵且主对角线元素全为1) 和 \(n\) 阶上三角矩阵 \(U\),使得 \(A=LU\) 则称其为矩阵 \(A\) 的 \(LU\) 分解,也称 Doolittle 分解。
通过例题的过程和上述的分析,可以进一步明确使用 \(LU\) 分解法求解线性方程组 \(Ax=b\) 的简要过程如下:
\[已知\ Ax=b,\ A=LU\\
则\ LUx=b\\
令\ y=Ux\\
有\ Ly=b\\
也就是求解\
\left\{
\begin{array}{l}
Ly=b\\
Ux=y
\end{array}
\right.
\]
显然上述的矩阵 \(L\) 为单位下三角矩阵, \(U\) 为上三角矩阵,计算均较为简便。
\(LU\) 分解的具体步骤如下:
第一步,令 \(l_{j1}=\frac{a^{(0)}_{j1}}{a^{(0)}_{11}}(1<j\leq n)\)
要求 \(a^{(0)}_{11}\neq0\),且从 \(A\) 的第 \(j\) 行减去第一行的 \(l_{j1}\)(称其为行乘数)倍,有
\[ L_1=
\left\{
\begin{matrix}
1&&&\\
-l_{21}&1&&\\
\vdots&&\ddots&\\
-l_{n1}&&&1
\end{matrix}
\right\}
\]
并且有
\[L_1A=
\left\{
\begin{matrix}
a_{11}^{(0)}&a_{12}^{(0)}&\cdots&a_{1n}^{(0)}\\
0&a_{22}^{(1)}&\cdots&a_{2n}^{(1)}\\
\vdots&\vdots&\cdots&\vdots\\
0&a_{n2}^{(1)}&\cdots&a_{nn}^{(1)}\\
\end{matrix}
\right\}
\]
第 k 步:
\[l_{jk}=\frac{a^{(k-1)}_{jk}}{a^{(k-1)}_{kk}}(k<j\leq n)\\
L_k=
\left\{
\begin{matrix}
1&&&&&&\\
&\ddots&&&&&\\
&&1&&&\\
&&-l_{k+1,k}&1&&\\
&&\vdots&&\ddots&\\
&&-l_{nk}&&&1\\
\end{matrix}
\right\}
\]
并且有
\[L_k\cdots L_2L_1A=
\left\{
\begin{matrix}
a_{11}^{(0)}&\cdots&a_{1k}^{(0)}&a_{1k+1}^{(0)}&\cdots&a_{1n}^{(0)}\\
&\ddots&\vdots&\vdots&&\vdots\\
&&a_{kk}^{(k-1)}&a_{kk+1}^{(k-1)}&\cdots&a_{kn}^{(k-1)}\\
&&&a_{k+1k+1}^{(k)}&\cdots&a_{k+1n}^{(k)}\\
&&&\vdots&\cdots&\vdots\\
&&&a_{nk+1}^{(k)}&\cdots&a_{nn}^{(k)}\\
\end{matrix}
\right\}
\]
最后有:
\[L_k\cdots L_2L_1A=
\left\{
\begin{matrix}
a_{11}^{(0)}&\cdots&a_{1k}^{(0)}&\cdots&a_{1n-1}^{(0)}&a_{1n}^{(0)}\\
&\ddots&\vdots&\vdots&&\vdots\\
&&a_{kk}^{(k-1)}&\cdots&a_{kn-1}^{(k-1)}&a_{kn}^{(k-1)}\\
&&&\ddots&\vdots&\vdots\\
&&&&a_{n-1n-1}^{(n-2)}&a_{n-1n}^{(n-2)}\\
&&&&&a_{nn}^{(n-1)}\\
\end{matrix}
\right\}
=U
\]
令 \(L=(L_{n-1}L_{n-2}\cdots L_2 L_1)^{-1}\)
\[L=
\left\{
\begin{matrix}
1&&&&\\
l_{21}&1&&&\\
\vdots&\vdots&\ddots&&\\
l_{n-11}&l_{n-12}&\cdots&1&\\
l_{n1}&l_{n2}&\cdots&l_{nn-1}&1
\end{matrix}
\right\}
\]
并且有 \(A=LU\)
通过上述分析,可以分析针对某一 \(n\) 阶线性方程组 \(Ax=b\),使用 \(LU\) 分解法求解的计算量与使用 Gauss 消去法求解的相同,只考虑乘除法时,为:
\[\frac{n^3}{3}+n^2-\frac{n}{3}
\]
若只考虑乘除法,与 \(\frac{n^3}{3}\) 是同阶的
若还考虑加减法,则与 \(\frac{2n^3}{3}\) 是同阶的。
* 例2 用 Doolittle 方法求解方程组
\[\left\{
\begin{matrix}
-3&2&6\\
10&-7&0\\
5&-1&5
\end{matrix}
\right\}
\left\{
\begin{matrix}
x_1\\x_2\\x_3
\end{matrix}
\right\}
=
\left\{
\begin{matrix}
4\\7\\6
\end{matrix}
\right\}
\]
解:
第一步,得到
\[\left\{
\begin{matrix}
1&0&0\\
\frac{10}{3}&1&0\\
\frac{5}{3}&0&1\\
\end{matrix}
\right\}
\left\{
\begin{matrix}
-3&2&6\\
10&-7&0\\
5&-1&5
\end{matrix}
\right\}
=
\left\{
\begin{matrix}
-3&2&6\\
0&-\frac{1}{3}&20\\
0&\frac{7}{3}&15
\end{matrix}
\right\}
\]
第二步,得到
\[\left\{
\begin{matrix}
1&0&0\\
0&1&0\\
0&7&1\\
\end{matrix}
\right\}
\left\{
\begin{matrix}
-3&2&6\\
0&-\frac{1}{3}&20\\
0&\frac{7}{3}&15
\end{matrix}
\right\}
=
\left\{
\begin{matrix}
-3&2&6\\
0&-\frac{1}{3}&20\\
0&0&155
\end{matrix}
\right\}
\]
得到 \(A=LU\)
\[L=\left\{
\begin{matrix}
1&0&0\\
\frac{10}{3}&1&0\\
\frac{5}{3}&7&1\\
\end{matrix}
\right\}\\
U=\left\{
\begin{matrix}
-3&2&6\\
0&-\frac{1}{3}&20\\
0&0&155
\end{matrix}
\right\}\\
A=LU=\left\{\begin{matrix}-3&2&6\\10&-7&0\\5&-1&5\end{matrix}\right\}
\]
回代求解方程组 \(Ly=b\)
\[\left\{
\begin{matrix}
1&0&0\\
\frac{10}{3}&1&0\\
\frac{5}{3}&7&1\\
\end{matrix}
\right\}
\left\{
\begin{matrix}
y_1\\y_2\\y_3
\end{matrix}
\right\}
=
\left\{
\begin{matrix}
4\\7\\6
\end{matrix}
\right\}
\]
得到 \(y_1=4,\ y_2=\frac{61}{3},\ y_3=155\)
回代求解方程组 \(Ux=y\)
\[\left\{
\begin{matrix}
-3&2&6\\
0&-\frac{1}{3}&20\\
0&0&155
\end{matrix}
\right\}
\left\{
\begin{matrix}
x_1\\x_2\\x_3
\end{matrix}
\right\}
=
\left\{
\begin{matrix}
4\\\frac{61}{3}\\155
\end{matrix}
\right\}\\
\]
最后得到原题中方程组的解为 \(x_1=0,\ x_2=-1,\ x_3=1\)
* 例3 利用 \(LU\) 分解求矩阵 \(A\) 的逆
\[A=
\left\{
\begin{matrix}
2&1&1&0\\
4&3&3&1\\
8&7&9&5\\
6&7&8&9\\
\end{matrix}
\right\}
\]
解:
设 \(A^{-1}=\{x_1,\ x_2, x_3,\ x_4\}\)
则 \(AA^{-1}=I\Leftrightarrow Ax_1=e_1,Ax_2=e_2,Ax_3=e_3,Ax_4=e_4\)
易得,经过 \(LU\) 分解后,有
\[A=LU=
\left\{
\begin{matrix}
1&&&\\
2&1&&\\
4&3&1&\\
3&4&1&1\\
\end{matrix}
\right\}
\left\{
\begin{matrix}
2&1&1&0\\
&1&1&1\\
&&2&2\\
&&&2\\
\end{matrix}
\right\}
\]
利用 \(\left\{
\begin{array}{l}
Ly_i=e_i\\
Ux_i=y_i
\end{array}
\right.\ i=1,\ 2,\ 3,\ 4\) 求解,有
\[Ly_1=e_1,\ Ux_1=y_1,\ x_1=\{\frac{9}{4},-3,-\frac{1}{2},\frac{3}{2}\}^T\\
Ly_2=e_2,\ Ux_2=y_2,\ x_2=\{-\frac{3}{4},\frac{5}{2},-1,-\frac{1}{2}\}^T\\
Ly_3=e_3,\ Ux_3=y_3,\ x_3=\{-\frac{1}{4},-\frac{1}{2},1,-\frac{1}{2}\}^T\\
Ly_4=e_4,\ Ux_4=y_4,\ x_4=\{\frac{1}{4},0,-\frac{1}{2},\frac{1}{2}\}^T\\
\]
则可以得到 \(A^{-1}\) 为
\[A^{-1}=
\left\{
\begin{matrix}
\frac{9}{4}&-\frac{3}{4}&-\frac{1}{4}&\frac{1}{4}\\
-3&\frac{5}{2}&-\frac{1}{2}&0\\
-\frac{1}{2}&-1&1&-\frac{1}{2}\\
\frac{3}{2}&-\frac{1}{2}&-\frac{1}{2}&\frac{1}{2}\\
\end{matrix}
\right\}
\]
Gauss 法与 LU 法计算量对比
对于单个方程组,计算量相同
对于多个线性方程组。即 \(Ax=b_1,\ b_2,\cdots, b_m\),构造增广矩阵使用 Gauss 法进行 1 次消去,使用 LU 法做 1 次分解,相同。
对于右端项无法直接列出的,使用 LU 法更简单。

LU 分解的存在和唯一性
显然,不是所有的矩阵都可以进行 LU 分解的,且可进行分解时分解不一定唯一,下述定理描述了LU分解的存在和唯一性;
存在性:在 A 的 1 至 n-1 阶顺序主子式均不为 0 的条件下, A 必有 LU 分解,即:
\[det
\begin{pmatrix}
\begin{bmatrix}
a_{11}&\cdots&a_{1i}\\
\vdots&\ddots&\vdots\\
a_{i1}&\cdots&a_{ii}\\
\end{bmatrix}
\end{pmatrix}
\neq0,\
i=1,\cdots,n-1
\]
唯一性:不论 A 为 非奇异还是其一矩阵,其 LU 分解唯一
相关的定理(矩阵的 LU 分解存在唯一性):如果 n 阶矩阵 A 的各阶顺序主子式 \(D_k(k=1,\cdots,n-1)\) 均不为零,则必有单位下三角矩阵 L 和上三角矩阵 U,使得 A=LU,而且 L 和 U 是唯一存在的。(这是一个充分条件)
* 例4
尝试对下列矩阵做 LU 分解,并判断是否唯一。
\[A=
\begin{Bmatrix}
1&2&3\\
2&4&1\\
4&6&7\\
\end{Bmatrix}
\xrightarrow{
\begin{Bmatrix}
1&&\\
-2&1&\\
-4&&1\\
\end{Bmatrix}
}
\begin{Bmatrix}
1&2&3\\
0&0&-5\\
0&-2&5\\
\end{Bmatrix}
\]
A 的前 2 阶顺序主子式为 1,0,不能做 LU 分解
\[B=
\begin{Bmatrix}
1&1&1\\
2&2&1\\
3&3&1\\
\end{Bmatrix}
\xrightarrow{
\begin{Bmatrix}
1&&\\
-2&1&\\
-3&&1\\
\end{Bmatrix}
}
\begin{Bmatrix}
1&2&3\\
0&0&-1\\
0&0&-2\\
\end{Bmatrix}
\]
B 的前 2 阶顺序主子式为 1,0,可以 LU 分解,但不唯一
\[C=
\begin{Bmatrix}
1&2&6\\
2&5&15\\
6&15&46\\
\end{Bmatrix}
\xrightarrow{
\begin{Bmatrix}
1&&\\
-2&1&\\
-6&&1\\
\end{Bmatrix}
}
\begin{Bmatrix}
1&2&6\\
0&1&3\\
0&3&1\\
\end{Bmatrix}
\xrightarrow{
\begin{Bmatrix}
1&&\\
0&1&\\
0&-3&1\\
\end{Bmatrix}
}
\begin{Bmatrix}
1&2&3\\
0&1&3\\
0&0&1\\
\end{Bmatrix}
\]
C 的前 2 阶顺序主子式为 1,1,可以做 LU 分解,且唯一
Doolittle 公式

LU, Crout, LDU 等分解及其存储
LU:
\[A=
\begin{Bmatrix}
a_{11}&a_{12}&\cdots&a_{1n}\\
a_{21}&a_{22}&\cdots&a_{2n}\\
&\cdots&\cdots&\\
a_{n1}&a_{n2}&\cdots&a_{nn}\\
\end{Bmatrix}
\]
\[L=\begin{Bmatrix}
1&&&\\
l_{21}&1&&\\
\vdots&\vdots&\ddots&\\
l_{n1}&l_{n2}&\cdots&1
\end{Bmatrix}
,\
U=\begin{Bmatrix}
u_{11}&u_{12}&\cdots&u_{1n}\\
&u_{1n}&\cdots&u_{2n}\\
&&\ddots&\vdots\\
&&&u_{nn}
\end{Bmatrix},\
\]
紧凑格式存储:
\[\begin{Bmatrix}
u_{11}&u_{12}&\cdots&u_{1n}\\
l_{21}&u_{22}&\cdots&u_{2n}\\
\vdots&\ddots&\ddots&\vdots\\
l_{n1}&\cdots&l_{n,n-1}&u_{nn}\\
\end{Bmatrix}
\]
也就是上三角存 U,下三角存 L;
Crout 分解:与 LU 分解类似,要求 L 是下三角矩阵,U 是单位上三角矩阵
\[\begin{Bmatrix}
a_{11}&a_{12}&\cdots&a_{1n}\\
a_{21}&a_{22}&\cdots&a_{2n}\\
\cdots&\cdots&\cdots&\cdots\\
a_{n1}&a_{n2}&\cdots&a_{nn}\\
\end{Bmatrix}
=
\begin{Bmatrix}
l_{11}&&&\\
l_{21}&l_{22}&&\\
\cdots&\cdots&\ddots&\\
l_{n1}&l_{n2}&\cdots&l_{nn}
\end{Bmatrix}
\begin{Bmatrix}
1&u_{12}&\cdots&u_{1n}\\
&1&\cdots&u_{2n}\\
&&\ddots&\vdots\\
&&&1
\end{Bmatrix}
\]
存储
\[\begin{Bmatrix}
l_{11}&u_{12}&\cdots&u_{1n}\\
l_{21}&l_{22}&\ddots&\vdots\\
\vdots&\ddots&\ddots&u_{n-1,n}\\
l_{n1}&\cdots&l_{n,n-1}&l_{nn}
\end{Bmatrix}
\]
LDU 分解:\(A=LDU\),其中 L 是单位下三角矩阵,U 是单位上三角矩阵,D 是一个非奇异的对角矩阵,则称矩阵 A 有 LDU 分解
\[\begin{Bmatrix}
a_{11}&a_{12}&\cdots&a_{1n}\\
a_{21}&a_{22}&\cdots&a_{2n}\\
\cdots&\cdots&\cdots&\cdots\\
a_{n1}&a_{n2}&\cdots&a_{nn}\\
\end{Bmatrix}
=
\begin{Bmatrix}
1&&&\\
l_{21}&1&&\\
\cdots&\cdots&\ddots&\\
l_{n1}&l_{n2}&\cdots&1
\end{Bmatrix}
\begin{Bmatrix}
d_1&&&\\
&d_2&&\\
&&\ddots&\\
&&&d_n
\end{Bmatrix}
\begin{Bmatrix}
1&u_{12}&\cdots&u_{1n}\\
&1&\cdots&u_{2n}\\
&&\ddots&\vdots\\
&&&1
\end{Bmatrix}
\]
存储
\[\begin{Bmatrix}
d_{1}&u_{12}&\cdots&u_{1n}\\
l_{21}&d_{2}&\ddots&\vdots\\
\vdots&\ddots&\ddots&u_{n-1,n}\\
l_{n1}&\cdots&l_{n,n-1}&d_{n}
\end{Bmatrix}
\]
* 例5
求
\[A=
\begin{Bmatrix}
2&1&1&0\\
4&3&3&1\\
8&7&9&5\\
6&7&9&8
\end{Bmatrix}
\]
的 Doolittle,Crout,LDU 分解
-
A 的 Doolittle 分解
\[\begin{Bmatrix}
2&1&1&0\\
4&3&3&1\\
8&7&9&5\\
6&7&9&8
\end{Bmatrix}
=
\begin{Bmatrix}
1&&&\\
2&1&&\\
4&3&1&\\
3&4&1&1
\end{Bmatrix}
\begin{Bmatrix}
2&1&1&0\\
&1&1&1\\
&&2&2\\
&&&2
\end{Bmatrix}
\]
-
A 的 Crout 分解
\[\begin{Bmatrix}
2&1&1&0\\
4&3&3&1\\
8&7&9&5\\
6&7&9&8
\end{Bmatrix}
=
\begin{Bmatrix}
2&&&\\
4&1&&\\
8&3&2&\\
6&4&2&8
\end{Bmatrix}
\begin{Bmatrix}
1&\frac{1}{2}&\frac{1}{2}&0\\
&1&1&1\\
&&1&-2\\
&&&1
\end{Bmatrix}
\]
-
A 的 LDU 分解
\[\begin{Bmatrix}
2&1&1&0\\
4&3&3&1\\
8&7&9&5\\
6&7&9&8
\end{Bmatrix}
=
\begin{Bmatrix}
1&&&\\
2&1&&\\
4&3&1&\\
3&4&1&1
\end{Bmatrix}
\begin{Bmatrix}
2&&&\\
&1&&\\
&&2&\\
&&&2
\end{Bmatrix}
\begin{Bmatrix}
1&\frac{1}{2}&\frac{1}{2}&0\\
&1&1&1\\
&&1&1\\
&&&1
\end{Bmatrix}
\]
Gauss 列主元消去法与带列主元的 LU 分解
一般方法可能存在问题:
- 有些有解的问题,不能用 Gauss 消元求解
- 如果某个 \(a_{kk}^{(k-1)}\) 很小的话,会引入大的误差
因此产生了改进,即选主元策略
Gauss 列主元消去法:为避免小主元作除数、或 0 作分母,在 Gauss 消去法中增加选主元的过程,即在第 k 步(\(k=1,2,\cdots,n-1\))消元时,首先在第 k 列主对角线下(含主对角元)元素中挑选绝对值对打的数,并通过初等行变换,使得该数位于主对角线上,然后再继续消元。称绝对值最大的数为列主元。将在消元过程中,每一步都按列选主元的 Gauss 消去法称之为 Gauss 列主元消去法。
带列主元的 LU 分解
一般情形:
如果 A 为 n 阶方阵,进行列主元 LU 分解过程为
\[L_{n-1}p_{n-1}\cdots L_2P_2L_1P_1A=U\Rightarrow(L_{n-1}\widetilde{L}_{n-2}\cdots \widetilde{L}_{2}\widetilde{L}_{1})(P_{n-1}\cdots P_2P_1)A=U
\]
其中,
\[\widetilde{L}_{k}=P_{n-1}\cdots P_{k+1}L_{k}P_{k+1}\cdots P_{n-1}
\]
令
\[L=(L_{n-1}\widetilde{L}_{n-2}\cdots \widetilde{L}_{2}\widetilde{L}_{1})^{-1}\ \ P=P_{n-1}\cdots P_2P_1\ \ 则 \ \ PA=LU
\]
矩阵列主元LU分解:对任意 n 阶矩阵 A,均存在置换矩阵 P、单位下三角矩阵 L 和上三角矩阵 U,使得 \(PA=LU\) 或 \(A=P^TLU\)(P, L 可以不同,分解不唯一)
LU 分解不一定存在
列主元 LU 分解一定存在,但不一定唯一
一般 LU 分解法求解线性方程组
\[A=LU \ \ \ \det(A)=\det(L)\det(U)=\det(U)\\
Ax=b\Leftrightarrow L(Ux)=b\Leftrightarrow
\left\{
\begin{array}{l}
Lc=b\\Ux=c
\end{array}
\right.
\]
列主元 LU 分解法求线性方程组
\[PA=LU\ \ \ \det(P)\det(A)=\det(PA)=\det(L)\det(U)=\det(u)\\
\det(P)=(-1)^s,\ \ s为换行次数\\
Ax=b\Leftrightarrow PAx=Pb\Leftrightarrow L(Ux)=Pb\Leftrightarrow
\left\{
\begin{array}{l}
Lc=Pb\\Ux=c
\end{array}
\right.
\]
* 例6
列主元消去法对矩阵 A 进行 LU 分解
\[A=
\begin{Bmatrix}
2&1&1&0\\
4&3&3&1\\
8&7&9&5\\
6&7&9&8
\end{Bmatrix}
\]
解:
第一次选列主元,交换第一行和第三行,A 左乘置换矩阵 \(P_1\) :
\[\begin{Bmatrix}
&&1&\\
&1&&\\
1&&&\\
&&&1
\end{Bmatrix}
\begin{Bmatrix}
2&1&1&0\\
4&3&3&1\\
8&7&9&5\\
6&7&9&8
\end{Bmatrix}
=
\begin{Bmatrix}
8&7&9&5\\
4&3&3&1\\
2&1&1&0\\
6&7&9&8
\end{Bmatrix}
\]
第一次消元,消去 A 第一列主元对角元以下的非零元,左乘矩阵 \(L_1\) :
\[\begin{Bmatrix}
1&&&\\
-\frac{1}{2}&1&&\\
-\frac{1}{4}&&1&\\
-\frac{3}{4}&&&1
\end{Bmatrix}
\begin{Bmatrix}
8&7&9&5\\
4&3&3&1\\
2&1&1&0\\
6&7&9&8
\end{Bmatrix}
=
\begin{Bmatrix}
8&7&9&5\\
&-\frac{1}{2}&-\frac{3}{2}&-\frac{3}{2}\\
&-\frac{3}{4}&-\frac{5}{4}&-\frac{5}{4}\\
&\frac{7}{4}&\frac{9}{4}&\frac{17}{4}
\end{Bmatrix}
\]
第二次选列主元,交换第二行和第四行,\(L_1P_1A\) 左乘置换矩阵 \(P_2\) :
\[\begin{Bmatrix}
1&&&\\
&&&1\\
&&1&\\
&1&&
\end{Bmatrix}
\begin{Bmatrix}
8&7&9&5\\
&-\frac{1}{2}&-\frac{3}{2}&-\frac{3}{2}\\
&-\frac{3}{4}&-\frac{5}{4}&-\frac{5}{4}\\
&\frac{7}{4}&\frac{9}{4}&\frac{17}{4}
\end{Bmatrix}
=
\begin{Bmatrix}
8&7&9&5\\
&\frac{7}{4}&\frac{9}{4}&\frac{17}{4}\\
&-\frac{3}{4}&-\frac{5}{4}&-\frac{5}{4}\\
&-\frac{1}{2}&-\frac{3}{2}&-\frac{3}{2}
\end{Bmatrix}
\]
第二次消元,消去 \(P_2L_1P_1A\) 第二列主元对角元以下的非零元,左乘矩阵 \(L_2\) :
\[\begin{Bmatrix}
1&&&\\
&1&&\\
&\frac{3}{7}&1&\\
&\frac{2}{7}&&1
\end{Bmatrix}
\begin{Bmatrix}
8&7&9&5\\
&\frac{7}{4}&\frac{9}{4}&\frac{17}{4}\\
&-\frac{3}{4}&-\frac{5}{4}&-\frac{5}{4}\\
&-\frac{1}{2}&-\frac{3}{2}&-\frac{3}{2}
\end{Bmatrix}
=
\begin{Bmatrix}
8&7&9&5\\
&\frac{7}{4}&\frac{9}{4}&\frac{17}{4}\\
&&-\frac{2}{7}&\frac{4}{7}\\
&&-\frac{6}{7}&-\frac{2}{7}
\end{Bmatrix}
\]
第三次选列主元,交换第三行和第四行,\(L_2P_2L_1P_1A\) 左乘置换矩阵 \(P_3\) :
\[\begin{Bmatrix}
1&&&\\
&1&&\\
&&&1\\
&&1&
\end{Bmatrix}
\begin{Bmatrix}
8&7&9&5\\
&\frac{7}{4}&\frac{9}{4}&\frac{17}{4}\\
&&-\frac{2}{7}&\frac{4}{7}\\
&&-\frac{6}{7}&-\frac{2}{7}
\end{Bmatrix}
=
\begin{Bmatrix}
8&7&9&5\\
&\frac{7}{4}&\frac{9}{4}&\frac{17}{4}\\
&&-\frac{6}{7}&-\frac{2}{7}\\
&&-\frac{2}{7}&\frac{4}{7}
\end{Bmatrix}
\]
第三次消元,消去 \(P_3L_2P_2L_1P_1A\) 第三列主元对角元以下的非零元,左乘矩阵 \(L_3\) :
\[\begin{Bmatrix}
1&&&\\
&1&&\\
&&1&\\
&&-\frac{1}{3}&1
\end{Bmatrix}
\begin{Bmatrix}
8&7&9&5\\
&\frac{7}{4}&\frac{9}{4}&\frac{17}{4}\\
&&-\frac{6}{7}&-\frac{2}{7}\\
&&-\frac{2}{7}&\frac{4}{7}
\end{Bmatrix}
=
\begin{Bmatrix}
8&7&9&5\\
&\frac{7}{4}&\frac{9}{4}&\frac{17}{4}\\
&&-\frac{6}{7}&-\frac{2}{7}\\
&&&\frac{2}{3}
\end{Bmatrix}
=U
\]
从而有 \(L_3(P_3L_2P_3^{-1})(P_3P_2L_1P_2^{-1}P_3^{-1})(P_3P_2P_1)A=U\)
且有 \(P_1=P_1^{-1}=P_1^T,\ P_2=P_2^{-1}=P_2^T,\ P_3=P_3^{-1}=P_3^T\)
记:
\[\widetilde{L}_2=P_3L_2P_3=
\begin{Bmatrix}
1&&&\\
&1&&\\
&\frac{2}{7}&1&\\
&\frac{3}{7}&&1
\end{Bmatrix}
\Leftarrow
L_2=
\begin{Bmatrix}
1&&&\\
&1&&\\
&\frac{3}{7}&1&\\
&\frac{2}{7}&&1
\end{Bmatrix}
\\
\widetilde{L}_1=P_3P_2L_1P_2P_3=
\begin{Bmatrix}
1&&&\\
-\frac{3}{4}&1&&\\
-\frac{1}{2}&&1&\\
-\frac{1}{4}&&&1
\end{Bmatrix}
\Leftarrow
L_1=
\begin{Bmatrix}
1&&&\\
-\frac{1}{2}&1&&\\
-\frac{1}{4}&&1&\\
-\frac{3}{4}&&&1
\end{Bmatrix}
\]
显然,\(\widetilde{L}_2\)和 \(\widetilde{L}_1\) 分别与 \(L_2\) 和 \(L_1\) 结构相同,只是下三角部分元素进行了相应的对调
从而有 \(L_3\widetilde{L}_2\widetilde{L}_1(P_3P_2P_1)A=U\Rightarrow(P_3P_2P_1)A=\widetilde{L}_1^{-1}\widetilde{L}_2^{-1}\widetilde{L}_3^{-1}U\)
令 \(P=P_3P_2P_1,\ L=\widetilde{L}_1^{-1}\widetilde{L}_2^{-1}\widetilde{L}_3^{-1}\)
则有
\[P=P_3P_2P_1=
\begin{Bmatrix}
0&0&1&0\\
0&0&0&1\\
0&1&0&0\\
1&0&0&0
\end{Bmatrix}
,\ \ \
L=\widetilde{L}_1^{-1}\widetilde{L}_2^{-1}\widetilde{L}_3^{-1}=
\begin{Bmatrix}
1&0&0&0\\
\frac{3}{4}&1&0&0\\
\frac{1}{2}&-\frac{2}{7}&1&0\\
\frac{1}{4}&-\frac{3}{7}&\frac{1}{3}&1
\end{Bmatrix}
\]
这样即得到 \(PA=LU\)
* 例7
用 Gauss 列主元消去法解如下方程组并给出 \(PA=LU\) 分解
解:
\[(A|b)=
\begin{Bmatrix}
0&-6&-1&-2\\
1&2&2&4\\
2&-2&1&1
\end{Bmatrix}
\xrightarrow{选列主元,交换第 1 和第 3 行}
\begin{Bmatrix}
2&-2&1&1\\
1&2&2&4\\
0&-6&-1&-2
\end{Bmatrix}
\\
\xrightarrow{第一次消元}
\begin{Bmatrix}
2&-2&1&1\\
0&3&\frac{3}{2}&\frac{7}{2}\\
0&-6&-1&-2
\end{Bmatrix}
\xrightarrow{选列主元,交换第2和第三行}
\begin{Bmatrix}
2&-2&1&1\\
0&-6&-1&-2\\
0&3&\frac{3}{2}&\frac{7}{2}
\end{Bmatrix}
\\
\xrightarrow{第二次消元}
\begin{Bmatrix}
2&-2&1&1\\
0&-6&-1&-2\\
0&0&1&\frac{5}{2}
\end{Bmatrix}
\]
用回代发求得解得:\(x=\{-\frac{5}{6},-\frac{1}{12},\frac{1}{2}\}^T\)
求相应的 \(PA=LU\) 分解
第一次选列主元,交换第 1 行和第 3 行,左乘置换矩阵 \(P_1\)
\[\begin{Bmatrix}
0&0&1\\
0&1&0\\
1&0&0
\end{Bmatrix}
\begin{Bmatrix}
0&-6&-1\\
1&2&2\\
2&-2&1
\end{Bmatrix}
=
\begin{Bmatrix}
2&-2&1\\
1&2&2\\
0&-6&-1
\end{Bmatrix}
\]
第一次消元,消去第一列主对角元以下的非零元,左乘 \(L_1\)
\[\begin{Bmatrix}
1&0&0\\
-\frac{1}{2}&1&0\\
0&0&1
\end{Bmatrix}
\begin{Bmatrix}
2&-2&1\\
1&2&2\\
0&-6&-1
\end{Bmatrix}
=
\begin{Bmatrix}
2&-2&1\\
0&3&\frac{3}{2}\\
0&-6&-1
\end{Bmatrix}
\]
第二次选列主元,交换第 2 行和第 3 行,左乘置换矩阵 \(P_2\)
\[\begin{Bmatrix}
1&0&0\\
0&0&1\\
0&1&0
\end{Bmatrix}
\begin{Bmatrix}
2&-2&1\\
0&3&\frac{3}{2}\\
0&-6&-1
\end{Bmatrix}
=
\begin{Bmatrix}
2&-2&1\\
0&-6&-1\\
0&3&\frac{3}{2}
\end{Bmatrix}
\]
第二次消元,消去第二列主对角元以下的非零元。左乘 \(L_2\)
\[\begin{Bmatrix}
1&0&0\\
0&1&0\\
0&\frac{1}{2}&1
\end{Bmatrix}
\begin{Bmatrix}
2&-2&1\\
0&-6&-1\\
0&3&\frac{3}{2}
\end{Bmatrix}
=
\begin{Bmatrix}
2&-2&1\\
0&-6&-1\\
0&0&1
\end{Bmatrix}
=U
\]
则分解应为
\[\begin{Bmatrix}
1&0&0\\
0&0&1\\
0&1&0
\end{Bmatrix}
\begin{Bmatrix}
0&0&1\\
0&1&0\\
1&0&0
\end{Bmatrix}
\begin{Bmatrix}
0&-6&-1\\
1&2&2\\
2&-2&1
\end{Bmatrix}
=
\begin{Bmatrix}
1&0&0\\
0&1&0\\
\frac{1}{2}&0&1
\end{Bmatrix}
\begin{Bmatrix}
1&0&0\\
0&1&0\\
0&-\frac{1}{2}&1
\end{Bmatrix}
\begin{Bmatrix}
2&-2&1\\
0&-6&-1\\
0&0&1
\end{Bmatrix}
\]
即有 \(PA=LU\)
\[\begin{Bmatrix}
0&0&1\\
1&0&0\\
0&1&0
\end{Bmatrix}
\begin{Bmatrix}
0&-6&-1\\
1&2&2\\
2&2&-1
\end{Bmatrix}
=
\begin{Bmatrix}
1&0&0\\
0&1&0\\
\frac{1}{2}&-\frac{1}{2}&1
\end{Bmatrix}
\begin{Bmatrix}
2&-2&1\\
0&-6&-1\\
0&0&1
\end{Bmatrix}
\]
对称正定矩阵 Cholesky 分解
对称正定矩阵 Cholesky 分解:对任意 n 阶对称正定矩阵 A,均存在下三角矩阵 L 使 \(A=LL^T\) 成立,称其为对称正定矩阵 A 的 Cholesky 分解,进一步地,如果规定 L 的对角元为正数,则 L 是唯一确定的。
若线性方程组 Ax=b 的系数矩阵是正定的,可按如下步骤求解:
- 求 A 的 Cholesky 分解 \(A=LL^T\)
- 求解:\(Ly=b\) 得 y
- 求解:\(L^Tx=y\)
平方根法通常是数值稳定的,不必选主元;且有 \(\det(A)=\det(L)\det(L^T)=\prod\limits^{n}_{k=1}l^2_{kk}\);运算量是 Gauss 消去法的一半,即 \(\frac{n^3}{6}\)
Cholesky 分解的计算公式
思想:利用矩阵乘法规则集矩阵 L 的下三角结构有:
\[\begin{Bmatrix}
a_{11}&\cdots&a_{1j}&\cdots&a_{1n}\\
\vdots&\ddots&\vdots&\ddots&\vdots\\
a_{i1}&\cdots&a_{ij}&\cdots&a_{in}\\
\vdots&\ddots&\vdots&\ddots&\vdots\\
a_{n1}&\cdots&a_{nj}&\cdots&a_{nn}\\
\end{Bmatrix}
=
\begin{Bmatrix}
l_{11}&\cdots&0&\cdots&0\\
\vdots&\ddots&\vdots&\ddots&\vdots\\
l_{i1}&\cdots&l_{ij}&\cdots&0\\
\vdots&\ddots&\vdots&\ddots&\vdots\\
l_{n1}&\cdots&l_{nj}&\cdots&l_{nn}\\
\end{Bmatrix}
\begin{Bmatrix}
l_{11}&\cdots&l_{1j}&\cdots&l_{1n}\\
\vdots&\ddots&\vdots&\ddots&\vdots\\
0&\cdots&l_{ij}&\cdots&l_{in}\\
\vdots&\ddots&\vdots&\ddots&\vdots\\
0&\cdots&0&\cdots&l_{nn}\\
\end{Bmatrix}
\]
得到:
\[a_{ij}=\sum\limits^{j-1}_{k=1}l_{ik}l_{jk}+l_{ij}l_{jj},\ i=j,j+1,\cdots,n
\]
首先,由 \(a_11=l_{11}^2\),得 \(l_{11}=\sqrt{a_{11}}\)
再有 \(a_{i1}=l_{11}l_{i1}\),得 \(l_{i1}=\frac{a_{i1}}{l_{11}},\ i=2,\cdots,n\)
这样便得到了矩阵 \(L\) 的第一列。假定已计算出 \(L\) 的第 \(j-1\) 列元素
由 \(a_{jj}=\sum\limits^{j-1}_{k=1}l^2_{jk}+l^2_{jj},\ j=1,\cdots,n\),得 \(l_{jj}=\sqrt{a_{jj}-\sum\limits^{j-1}_{k=1}l^2_{jk}}\)
再由 \(a_{ij}=\sum\limits^{j-1}_{k=1}l_{ik}l_{jk}+l_{ij}l_{jj},\ i=j+1,\cdots,n\),得 \(l_{ij}=(a_{ij}-\sum\limits^{j-1}_{k=1}l_{ik}l_{jk})/l_{jj}\)
- 对矩阵 A 进行 Cholesky 分解,即 \(A=LL^T\),对于 \(j=1,2,\cdots,n\) 计算:
\[l_{jj}=\sqrt{a_{jj}-\sum\limits^{j-1}_{k=1}l^2_{jk}}\\
l_{ij}=(a_{ij}-\sum\limits^{j-1}_{k=1}l_{ik}l_{jk})/l_{jj}\\
i=j+1,j+2,\cdots,n
\]
计算次序为:
\[l_{11},l_{21},\cdots,l_{n1},l_{22},l_{32},\cdots,l_{n2},\cdots,l_{nn}
\]
即:顺次逐列计算下三角矩阵 L 的每一列,先求对角线元素 \(l_{jj}\),再求此列后续元素 \(l_{ij}\)
-
求解下三角形方程组 \(Ly=b\) 得 \(y\)
\[y_1=b_1/l_{11}\\
y_i=(b_i-\sum\limits^{i-1}_{k=1}l_{ik}y_k)/l_{ii}\\
i=2,3,\cdots,n
\]
-
求解上三角形方程组 \(L^Tx=y\) 得 \(x\)
\[x_n=y_n/l_{nn}\\
x_i=(y_i-\sum\limits^{n}_{k=i+1}l_{ki}x_k)/l_{ii}\\
i=n-1,n-2,\cdots,1
\]
其他:
- 由于 A 的元素 \(a_{ij}\) 被用来计算出 \(l_{ij}\) 后不再使用,所以可将 L 的元素存储在 A 的对应位置上;
- \(LD^TL\) 分解(Cholesky 分解的变形):为避免开方运算,可以求 \(A=LD^TL\),其中 L 是单位下三角矩阵,D 是对角元素均为正数的对角矩阵
* 例8
用 Cholesky 方法阶线性方程组 Ax=b,其中
\[A=
\begin{Bmatrix}
4&-1&1\\
-1&4.25&2.75\\
1&2.75&3.5
\end{Bmatrix}
\ \ \ \ \ \ \ \ \
b=
\begin{Bmatrix}
4\\6\\7.25
\end{Bmatrix}
\]
解:
显然 \(A^T=A\),且 \(D_1=4>0,\ D_2=16>0,\ D_3=16>0\)。因此 A 为对称正定矩阵,故存在 \(A=LL^T\)。由分解公式依次计算出 L 的各个元素:
\[l_{11}=\sqrt{a_{11}},\ l_{21}=\frac{a_{21}}{l_{11}}=-0.5,\ l_{31}=\frac{a_{31}}{l_{11}}=0.5\\
l_{22}=\sqrt{a_{22}-l^2_{21}}=\sqrt{4.25-0.5^2}=2,\ l_{32}=\frac{a_{32}-l_{31}l_{21}}{l_{22}}=(2.75-(-0.5)\times 0.5)/2=1.5\\
l_{33}=\sqrt{a_{33}-l_{31}^2-l_{32}^2}=\sqrt{3.5-0.5^2-1.5^2}=1
\]
从而得:
\[L=
\begin{Bmatrix}
2&&\\
-0.5&2&\\
0.5&1.5&1
\end{Bmatrix}
\]
再求下三角方程组 \(Ly=b\) 的解,得:
\[y_1=\frac{b_1}{l_{11}}=\frac{4}{2}=2,\ y_2=\frac{b_2-l_{21}\cdot y_1}{l_{22}}=\frac{6+1}{2}=3.5\\
y_3=\frac{b_3-l_{31}\cdot y_1-l_{32}\cdot y_2}{l_{33}}=7.25-0.5\times 2-1.5\times 3.5=1\\
y=\{2,3.5,1\}^T
\]
最后求上三角方程组 \(L^Tx=y\) 的解,得:
\[x_1=\frac{y_3}{l_{33}}=\frac{1}{1}=1,\ x_2=\frac{y_2-l_{32}\cdot x_2}{l_{22}}=\frac{3.5-1.5}{2}=1\\
x_3=\frac{y_1-l_{21}\cdot x_2-l_{31}\cdot x_3}{l_{11}}=0.5\times(2+0.5-0.5)=1\\
y=\{1,1,1\}^T
\]
三对角矩阵的三角分解
设三对角矩阵
\[A=
\begin{Bmatrix}
b_1&c_1&&&\\
a_2&b_2&c_2&&\\
&\ddots&\ddots&\ddots&\\
&&a_{n-1}&b_{n-1}&c_{n-1}\\
&&&a_n&b_n
\end{Bmatrix}
\]
如果矩阵 A 可以进行 LU 分解 A=LU,其中
\[L=
\begin{Bmatrix}
1&&&&\\
l_2&1&&&\\
&l_3&\ddots&&\\
&&\ddots&1&\\
&&&l_n&1
\end{Bmatrix}
,\ \
U=
\begin{Bmatrix}
u_1&d_1&&&\\
&u_2&d_2&&\\
&&\ddots&\ddots&\\
&&&u_{n-1}&d_{n-1}\\
&&&&u_n
\end{Bmatrix}
\]
则有
\[A=LU\\
A=
\begin{Bmatrix}
b_1&c_1&&&\\
a_2&b_2&c_2&&\\
&\ddots&\ddots&\ddots&\\
&&a_{n-1}&b_{n-1}&c_{n-1}\\
&&&a_n&b_n
\end{Bmatrix}
=
\begin{Bmatrix}
1&&&&\\
l_2&1&&&\\
&l_3&\ddots&&\\
&&\ddots&1&\\
&&&l_n&1
\end{Bmatrix}
\begin{Bmatrix}
u_1&d_1&&&\\
&u_2&d_2&&\\
&&\ddots&\ddots&\\
&&&u_{n-1}&d_{n-1}\\
&&&&u_n
\end{Bmatrix}
\\
=
\begin{Bmatrix}
u_1&d_1&&&\\
l_2u_1&l_2d_1+u_2&d_2&&\\
&\ddots&\ddots&\ddots&\\
&&l_{n-1}u_{n-2}&u_{n-1}&d_{n-1}\\
&&&l_nu_{n-1}&l_nd_{n-1}+u_n
\end{Bmatrix}
\]
追赶法解三对角矩阵的算法:
对 A 进行 LU 分解,公式如下:
\[\left\{
\begin{array}{ml}
d_i=c_i,\ &i=1,2,\cdots,n-1\\
u_1=b_1\\
l_i=\frac{a_i}{u_{i-1}},\ &i=2,3,\cdots,n\\
u_i=b_i-l_ic_{i-1},\ &i=2,3,\cdots,n
\end{array}
\right.
\]
计算次序是
\[u_1\rightarrow l_2\rightarrow u_2\rightarrow l_3\rightarrow u_3\rightarrow \cdots\rightarrow l_n\rightarrow u_n
\]
LU 分解的计算量:乘除法 \(2(n-1)\),加减法 \(n-1\)
求解下三角形方程组 \(Ly=f\)
\[\begin{Bmatrix}
1&&&&\\
l_2&1&&&\\
&l_3&\ddots&&\\
&&\ddots&1&\\
&&&l_n&1
\end{Bmatrix}
\begin{Bmatrix}
y_1\\y_2\\\vdots\\y_{n-1}\\y_n
\end{Bmatrix}
=
\begin{Bmatrix}
f_1\\f_2\\\vdots\\f_{n-1}\\f_n
\end{Bmatrix}
\]
\[y_1=f_1,\ l_iy_{i-1}+y_i=f_i,\ y_i=f_i-l_i\cdot y_{i-1},\ i=2,3,\cdots,n
\]
计算量:乘除法 \(n-1\),加减法\(n-1\)
求解上三角形方程组
\[\begin{Bmatrix}
u_1&d_1&&&\\
&u_2&d_2&&\\
&&\ddots&\ddots&\\
&&&u_{n-1}&d_{n-1}\\
&&&&u_n
\end{Bmatrix}
\begin{Bmatrix}
x_1\\x_2\\\vdots\\x_{n-1}\\x_n
\end{Bmatrix}
=
\begin{Bmatrix}
y_1\\y_2\\\vdots\\y_{n-1}\\y_n
\end{Bmatrix}
\]
\[x_n=y_n/u_n,\ u_i\cdot x_i+d_ix_{i+1}=y_i,\ x_i=(y_i-d_ix_{i+1})/u_i,\ i=n-1,n-2,\cdots,1
\]
解方程计算量:乘除法 \(2(n-1)+1\),加减法 \(n-1\)
追赶法的使用条件:
设具有三对角形式的矩阵 A,满足条件
- \(|b_1|>|c_1|>0\)
- \(|b_n|>|a_n|>0\)
- \(|b_i|\geq|a_i|+|c_i|,\ a_ic_i\neq0,\ i=2,3,\cdots,n-1\) (对角占优)
则方程组 \(Ax=f\) 可用追赶法求解,且解存在唯一
其他:
- 计算量小,共 \(8n-7\) 次四则运算
- 存储量小,仅需要 4 个一维数组 a, b, c, f, 其中, d,l,u,x 分别存在 c,a,b,f 中
- 当 A 为对角占优时,数值稳定(中间数有界)
* 例9
用追赶法解线性方程组 \(Ax=b\),其中
\[A=
\begin{Bmatrix}
4&-1&0\\
-1&4&-1\\
0&-1&4
\end{Bmatrix}
,\ \ b=
\begin{Bmatrix}
1\\2\\3
\end{Bmatrix}
\]
解:
\(d_1=c_1=-1\),依次计算出 \(u_1,l_2,u_2,l_3,u_3\) 诸元素:
\[b_1=u_1=4,\ l_2=\frac{a_2}{u_1}=-0.25\\
u_2=b_2-l_2c_1=4-(-0.25)\times(-1)=3.75\\
l_3=\frac{a_3}{u_2}=\frac{-1}{3.75}=-0.2667\\
u_3=b_3-l_3c_2=4-(-0.2667)\times(-1)=4.7331\\
L=
\begin{Bmatrix}
1&0&0\\
-0.25&1&0\\
0&-0.2667&1
\end{Bmatrix}
,\ \
U=
\begin{Bmatrix}
4&-1&0\\
0&3.75&-1\\
0&0&3.7333
\end{Bmatrix}
\]
求下三角线性方程组 \(Ly=b\) 的解,即:
\[y_1=1,\ y_2=f_2-l_2\cdot y_1=3+0.25=3.25\\
y_3=f_3-l_3\cdot y_2=2+0.2667\times 3.25=2.8667\\
y=
\begin{Bmatrix}
1,3.25,2.8667
\end{Bmatrix}^T
\]
求上三角线性方程组 \(Ux=y\) 的解,即:
\[x_3=\frac{y_3}{u_3}=0.7679,\ x_2=\frac{y_2-c_2\cdot x_3}{u_2}=1.0714\\
x_1=\frac{y_1-c_1\cdot x_2}{u_1}=0.5179\\
x=
\begin{Bmatrix}
0.7679,1.0714,0.5179
\end{Bmatrix}^T
\]
条件数与方程组的形态
定义:如果线性方程组 \(Ax=b\) 中,A 或 b 的元素的微小变化就会引起方程组解的巨大变化,则称方程组为病态方程组,矩阵 A 称为病态矩阵,否则称方程组为良态方程组,矩阵称为良态矩阵
敏度分析:研究计算问题的原始数据有微小的改变将会引起解的多大变化;
敏度分析目的:寻找刻画问题“病态”标准的量
矩阵条件数:设 A 为非奇异矩阵,\(||\cdot||\) 为矩阵的算子范数,则称 \(cond(A)=||A||\ ||A^{-1}||\) 为矩阵 A 的条件数
以矩阵 A 为例,常用的条件数有:
-
矩阵 A 的 \(\infty-条件数\):\(cond_\infty(A)=||A||_\infty\ ||A^{-1}||_\infty\)
-
矩阵 A 的 \(1-条件数\):\(cond_1(A)=||A||_1\ ||A^{-1}||_1\)
-
矩阵 A 的 \(2-条件数\):\(cond_2(A)=||A||_2\ ||A^{-1}||_2=\sqrt{\frac{\lambda_\max(A^HA)}{\lambda_\min(A^HA)}}\)
条件数的性质:
-
非负性?\(cond(A)\geq1\)
\(cond(A)=||A^{-1}||\ ||A||\geq||A^{-1}A||=||I||=1\)
-
齐次性?\(cond(\alpha A)=cond(A),\ \alpha\neq0,\ \alpha\in R\)
\(aond(\alpha A)=||\alpha A||\ ||(\alpha A)^{-1}||=|\alpha|\cdot||A||\cdot\frac{1}{|\alpha|}\cdot||A^{-1}||=cond(A)\)
-
三角不等式? 没有确定结论
\(cond(A+B)=||A+B||\ ||(A+B)^{-1}||\ \ ||A||\ ||A^{-1}||+||B||\ ||B^{-1}||=cond(A)+cond(B)\)
-
相容性? \(cond(AB)\leq cond(A)\cdot cond(b)\)
\(cond(AB)=||AB||\ ||(AB)^{-1}||\leq ||A||\cdot||B||\cdot||A^{-1}||\cdot||B^{-1}||=cond(A)\cdot cond(B)\)
-
\(cond(A)=cond(A^{-1})\)
\(cond(A^{-1})=||A^{-1}||\cdot||(A^{-1})^{-1}||=||A^{-1}||\cdot||A||=cond(A)\)
-
如果 U 为酉(正交)矩阵,则
\(cond_2(U)=1\ \ cond_2(UA)=cond_2(AU)=cond_2(A)\)
cond(A) 越大,接的相对误差界可能越大,对求解线性方程组来说就越可能呈现病态;cond(A) 多大算病态,通常没有具体的定量标准;cond(A) 越小,解的相对误差界越小,呈现良态
* 例10
求对称正定矩阵 H 的条件数 \(cond_\infty(H)\)
解:
\[H=
\begin{Bmatrix}
\frac{1}{2}&\frac{1}{3}&\frac{1}{4}\\
\frac{1}{3}&\frac{1}{4}&\frac{1}{5}\\
\frac{1}{4}&\frac{1}{5}&\frac{1}{6}
\end{Bmatrix}
\ \
H^{-1}=
\begin{Bmatrix}
72&-240&180\\
-240&900&-720\\
180&-720&600
\end{Bmatrix}
\\
||H||_\infty=\frac{13}{12},\ ||H^{-1}||=1860,\ cond_\infty(H)=2.015\times10^3
\]
* 例11
数据拟合函数逼近中的 Hilbert 矩阵
解:
\[H_n=(h_{ij})_{n\times n}=
\begin{Bmatrix}
1&\frac{1}{2}&\cdots&\frac{1}{n}\\
\frac{1}{2}&\frac{1}{3}&\cdots&\frac{1}{n+1}\\
\vdots&\vdots&\cdots&\vdots\\
\frac{1}{n}&\frac{1}{n+1}&\cdots&\frac{1}{2n-1}\\
\end{Bmatrix}
\\
cond_2(H_4)=1.5514\times 10^4,\ cond_2(H_6)=1.4951\times 10^7,\ cond_2(H_8)=1.525\times 10^{10}
\]
* 例12
求 \(A=\begin{Bmatrix}1&6\\2&6.00001\end{Bmatrix}\ \ b=\begin{Bmatrix}8\\8.00001\end{Bmatrix}\) 的条件数
解:
\[A^{-1}=
\begin{Bmatrix}
300000.5&-300000\\
-100000&100000
\end{Bmatrix}
\]
则 A 的条件数为:
\[\begin{aligned}
cond_\infty(A)&=||A||_\infty||A^{-1}||_\infty\\
&=8.00001\times600000.5\\
&\approx4.8\times10^6
\end{aligned}
\]
解的相对误差界为:
\[\delta b=(0.00001)^T
\]
\[\begin{aligned}
\frac{||\delta x||_\infty}{||x||_\infty}&\leq cond_\infty(A)\frac{||\delta b||_\infty}{||b||_\infty}\\
&\approx4.8\times10^6\times\frac{0.00001}{8.00001}\\
&\approx6\approx600\%
\end{aligned}
\]
定理:对于线性方程组 Ax=b,A 为非奇异矩阵,\(\delta A\) 和 \(\delta b\) 分别为 A 和 b 的扰动。若扰动 \(\delta A\)非常小,使得 \(||A||^{-1}\ ||\delta A||<1\),则 \(\frac{||\delta x||}{||x||}\leq\frac{||A||\ ||A^{-1}||}{1-||A^{-1}||\ ||\delta A||}(\frac{||\delta A||}{||A||}+\frac{||\delta b||}{||b||})\)
余量和误差:
-
称 \(||b-A\tilde{x}||\) 为近似解 \(\tilde{x}\) 的余量
-
称 \(||x-\tilde{x}||\) 为近似解 \(\tilde{x}\) 的误差
-
设 Ax=b,A 为非奇异矩阵,b 为非零向量,则方程组近似解 \(\tilde{x}\) 的时候误差估计式为:
\[\frac{1}{cond(A)}\frac{||b-A\tilde{x}||}{||b||}\leq\frac{||\tilde{x}-x||}{||x||}\leq cond(A)\frac{||b-A\tilde{x}||}{||b||}
\]
-
若 \(cond(A)\approx1\) 时,余量的相对误差可作为解的相对误差的一个好的度量
-
对于病态方程组,虽然余量的相对误差易筋经很小,但解的相对误差仍然很大
条件数的几何意义:
设方阵 A 为非奇异,则 \(\min\{\frac{||\delta A||_2}{||A||_2}:A+\delta A奇异\}=\frac{1}{||A^{-1}||_2\cdot||A||_2}=\frac{1}{cond_2(A)}\),即在谱范数下,一个矩阵的条件数的倒数正好等于该矩阵与全体奇异矩阵所成集合的相对距离。
当矩阵十分病态时,就说明该矩阵已经十分接近一个奇异矩阵
矩阵的 QR 分解
LU 分解不一定可以保持条件数
利用正交变换实现矩阵分解 \(A=QR\),Q 为正交阵,R 为上三角阵
\[Ax=b\xrightarrow{A=QR}
\left\{
\begin{array}{ml}
Qy=b\\
Rx=y
\end{array}
\right.
\Leftrightarrow
Rx=Q^Tb
\]
QR 分解:如果 \(A\in R^{m\times n}(m\geq n),\ r(A)=n\),\(A=Q\begin{Bmatrix}R_1\\O\end{Bmatrix}=QR\) 其中 \(Q\) 为正交阵,\(R_1\) 为对角元非零的上三角矩阵
QR 分解的步骤:(具体过程可参照 *例12,*例13)
- 计算 QR 因子分解 A=QR
- 计算 \(y=Q^Tb\)
- 对 x 解 Rx=y
从几何上看,就是把空间中的一个向量通过正交变换,变成落在第一个坐标轴上的向量
Householder 矩阵(H 阵):设 \(\omega\in R^n,\ \omega\neq0\),称初等矩阵 \(H(\omega)=I-\frac{2}{\omega^T\omega}\omega\omega^T\) 为 Householder 矩阵,或称其为 Householder 变换,Householder 矩阵是一种特殊的初等变换矩阵
Householder 矩阵的性质:
-
对称性 \(H(\omega)^T=H(\omega)\)
\[H(\omega)^T=(I-\frac{2}{\omega^T\omega}\omega\omega^T)^T=I-\frac{2}{\omega^T\omega}(\omega\omega^T)^T=I-\frac{2}{\omega^T\omega}\omega\omega^T=H(\omega)
\]
-
正交性 \(H(\omega)^TH(\omega)=I\)
\[\begin{aligned}
H(\omega)^TH(\omega)&=(I-\frac{2}{\omega^T\omega}\omega\omega^T)^2=I-\frac{2}{\omega^T\omega}\omega\omega^T-\frac{2}{\omega^T\omega}\omega\omega^T+(\frac{2}{\omega^T\omega})^2(\omega\omega^T)(\omega\omega^T)\\
&=I-\frac{4}{\omega^T\omega}\omega\omega^T+\frac{4}{(\omega^T\omega)^2}\omega(\omega^T\omega)\omega^T\\&=I
\end{aligned}
\]
-
\(H(\omega)\) 为特征值为 n-1 个 1 和一个 -1
\[|H(\omega)|=-1
\]
-
如果 \(H(\omega)x=y\),则 \(||y||_2=||x||_2\)(长度不变)
\[||y||^2_2=y^Ty=(H(\omega)x)^T(H(\omega)x)=x^T(H(\omega)^TH(\omega))x=x^Tx=||x||^2_2
\]
-
设 \(x,y\in R^n,x\neq y,||x||_2=||y||_2\),取 \(\omega=x-y\),则 \(H(\omega)x=y\)
-
设 \(x=(x_1,x+2,\cdots,x_n)^T\in R^n\) 且 \(x\neq 0\),取 \(\omega=x\pm||x||_2e_1\) 则 \(H(\omega)x=\mp||x||_2e_1\)
事实上,变换后的向量可以为 \(\pm||x||_2e_1\)
- 正负号的选取
- 正负号强制选取
- 向量 x 的数量级较大
-
设 \(x=(x_1,x_2,\cdots,x_n)^T\in C^n\) 且 \(x\neq0\),取 \(\omega=x-\alpha e_1\),其中 \(|\alpha|=||x||_2\),且 \(\alpha x^He_1\) 为实数,则 \(H(\omega)=\alpha e_1\)
* 例11
求 Householder 矩阵 H,使得 Hx=y
(1)\(x=(-3,0,4)^T,\ y=(0,0,5)^T\)
(2)\(x=(i,-2i,0,2)^T,y=(\alpha,0,0,0)^T\)
解:
(1)
\[\omega=x-y=(-3,0,-1)^T\ \ \omega^T\omega=10\\
H(\omega)=I-2\frac{\omega\omega^T}{\omega^T\omega}=
\begin{Bmatrix}
1&&\\&1&\\&&1
\end{Bmatrix}
-\frac{2}{10}
\begin{Bmatrix}
-3\\0\\1
\end{Bmatrix}
\begin{Bmatrix}
-3,0,-1
\end{Bmatrix}
=
\begin{Bmatrix}
-\frac{4}{5}&0&-\frac{3}{5}\\
0&1&0\\
-\frac{3}{5}&0&\frac{4}{5}
\end{Bmatrix}
\]
(2)
确定 \(\alpha\),需满足 \(|\alpha|=||x||_2=\sqrt{1+4+0+4}=3,\ \alpha x^H e_1=-\alpha i\),故 \(\alpha=\pm3i\)
以 \(\alpha=3i\) 为例
\[\omega=x-y=(-2i,-2i,0,2)^T\ \ \omega^T\omega=12\\
H(\omega)=I-2\frac{\omega\omega^T}{\omega^T\omega}=
\begin{Bmatrix}
1&&&\\
&1&&\\
&&1&\\
&&&1
\end{Bmatrix}
-\frac{2}{12}
\begin{Bmatrix}
-2i\\ -2i\\0\\2
\end{Bmatrix}
\begin{Bmatrix}
-2i,-2i,0,2
\end{Bmatrix}
=\frac{1}{3}
\begin{Bmatrix}
1&-2&0&2i\\
-2&1&0&2i\\
0&0&3&0\\
-2i&-2i&0&1
\end{Bmatrix}
\]
* 例12
利用 Householder 变换求 A 的分解,其中
\[A=
\begin{Bmatrix}
1&1&1\\
2&3&1\\
2&1&-5
\end{Bmatrix}
\]
解:
\[a_1=\begin{Bmatrix}
1\\2\\2
\end{Bmatrix},\ ||a_1||_2=3\\
\omega_1=a_1-||a_1||_2e_1=\begin{Bmatrix}1\\2\\2\end{Bmatrix}-\begin{Bmatrix}3\\0\\0\end{Bmatrix}=\begin{Bmatrix}-2\\2\\2\end{Bmatrix}\\
Q_1=H(\omega_1)=I-\frac{2}{\omega_1^T\omega_1}\omega_1\omega_1^T=
\begin{Bmatrix}
\frac{1}{3}&\frac{2}{3}&\frac{2}{3}\\
\frac{2}{3}&\frac{1}{3}&\frac{-2}{3}\\
\frac{2}{3}&\frac{-2}{3}&\frac{1}{3}
\end{Bmatrix}\\
Q_1A=
\begin{Bmatrix}
3&3&-\frac{7}{3}\\
0&1&\frac{13}{3}\\
0&-1&-\frac{5}{3}
\end{Bmatrix}
=
\begin{Bmatrix}
3&b^T\\
0&A_2
\end{Bmatrix}\\
\tilde{a_1}=
\begin{Bmatrix}
1\\ -1
\end{Bmatrix}
,\ ||\tilde{a_1}||_2=\sqrt{2},\\
\tilde{\omega}_2=\tilde{a_1}-||\tilde{a_1}||_2e_1=\begin{Bmatrix}1\\ -1\end{Bmatrix}-\begin{Bmatrix}\sqrt2\\0\end{Bmatrix}=
\begin{Bmatrix}
1-\sqrt{2}\\ -1
\end{Bmatrix}\\
\tilde{Q_2}=H(\tilde{\omega_2})=I-\frac{2}{\tilde{\omega_2}^T\tilde{\omega_2}}\tilde{\omega_2}\tilde{\omega_2}^T=\frac{1}{2}
\begin{Bmatrix}
\sqrt{2}&-\sqrt{2}\\
-\sqrt{2}&-\sqrt{2}
\end{Bmatrix},\\
\tilde{Q_2}A_2=(H(\tilde{\omega_2})\tilde{a_1},H(\tilde{\omega_2})\tilde{a_2})=
\begin{Bmatrix}
\sqrt{2}&3\sqrt{2}\\
0&-\frac{4}{3}\sqrt{2}
\end{Bmatrix}
\\
Q_2=\begin{Bmatrix}
1&0^T\\
0&\tilde{Q_2}
\end{Bmatrix}
\]
\[Q_2Q_1A=Q_2
\begin{Bmatrix}
3&b^T\\
0&A_2
\end{Bmatrix}
=
\begin{Bmatrix}
3&b^T\\0&\tilde{Q_2}A_2
\end{Bmatrix}
=\begin{Bmatrix}
3&3&-\frac{7}{3}\\
0&\sqrt{2}&3\sqrt{2}\\
0&0&-\frac{4}{3}\sqrt{2}
\end{Bmatrix}
=R\\
Q=(Q_2Q_1)^T=
\begin{Bmatrix}
\frac{1}{3}&\frac{2}{3}&\frac{2}{3}\\
\frac{2}{3}&\frac{1}{3}&\frac{-2}{3}\\
\frac{2}{3}&\frac{-2}{3}&\frac{1}{3}
\end{Bmatrix}
\begin{Bmatrix}
1&0&0\\
0&\frac{\sqrt{2}}{2}&-\frac{\sqrt{2}}{2}\\
0&-\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}
\end{Bmatrix}
=
\begin{Bmatrix}
\frac{1}{3}&0&-\frac{2\sqrt{2}}{3}\\
\frac{2}{3}&\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{6}\\
\frac{2}{3}&-\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{6}
\end{Bmatrix}
\\
\begin{aligned}
A=QR&=
\begin{Bmatrix}
\frac{1}{3}&0&-\frac{2\sqrt{2}}{3}\\
\frac{2}{3}&\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{6}\\
\frac{2}{3}&-\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{6}
\end{Bmatrix}
\begin{Bmatrix}
3&3&-\frac{7}{3}\\
0&\sqrt{2}&3\sqrt{2}\\
0&0&-\frac{4}{3}\sqrt{2}
\end{Bmatrix}\\
(如果想调整 R的对角元的符号)&=
\begin{Bmatrix}
\frac{1}{3}&0&-\frac{2\sqrt{2}}{3}\\
\frac{2}{3}&\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{6}\\
\frac{2}{3}&-\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{6}
\end{Bmatrix}
\begin{Bmatrix}
1&0&0\\0&1&0\\0&0&-1
\end{Bmatrix}
\begin{Bmatrix}
1&0&0\\0&1&0\\0&0&-1
\end{Bmatrix}
\begin{Bmatrix}
3&3&-\frac{7}{3}\\
0&\sqrt{2}&3\sqrt{2}\\
0&0&-\frac{4}{3}\sqrt{2}
\end{Bmatrix}\\
&=\begin{Bmatrix}
\frac{1}{3}&0&\frac{2\sqrt{2}}{3}\\
\frac{2}{3}&\frac{\sqrt{2}}{2}&-\frac{\sqrt{2}}{6}\\
\frac{2}{3}&-\frac{\sqrt{2}}{2}&-\frac{\sqrt{2}}{6}
\end{Bmatrix}
\begin{Bmatrix}
3&3&-\frac{7}{3}\\
0&\sqrt{2}&3\sqrt{2}\\
0&0&\frac{4}{3}\sqrt{2}
\end{Bmatrix}=\tilde{Q}\tilde{R}
\end{aligned}
\]
* 例13
利用 Householder 变换求 A 的分解,其中
(1)\(A=\begin{Bmatrix}0&4&1\\1&1&1\\0&3&2\end{Bmatrix}\)
(2)\(A=\begin{Bmatrix}0&4\\0&0\\5&2\end{Bmatrix}\)
解:
(1)
\[A=(a_1,a_2,a_3),\ a_1=\begin{Bmatrix}0\\1\\0\end{Bmatrix}\ ||a_1||_2=1\\
\omega=a_1-||a_1||_2e_1=\begin{Bmatrix}0\\1\\0\end{Bmatrix}-\begin{Bmatrix}1\\0\\0\end{Bmatrix}=\begin{Bmatrix}-1\\1\\0\end{Bmatrix}\\
Q_1=H(\omega_1)=I-\frac{2}{\omega^T_1\omega_1}\omega_1\omega_1^T=
\begin{Bmatrix}
0&1&0\\1&0&0\\0&0&1
\end{Bmatrix}\\
Q_1A=H(\omega_1)=(H(\omega)_1a_1,H(\omega)_1a_2,H(\omega)_1a_3)=
\begin{Bmatrix}
1&1&1\\0&4&1\\0&3&2
\end{Bmatrix}
=
\begin{Bmatrix}
1&b^T\\0&A_2
\end{Bmatrix}\\
A_2=\begin{Bmatrix}4&1\\3&2\end{Bmatrix}=\{\tilde{a_1},\tilde{a_2}\},\ ||\tilde{a_1}||_2=5\\
\omega_2=\tilde{a_1}-||\tilde{a_1}||_2e_1=\begin{Bmatrix}4\\3\end{Bmatrix}-\begin{Bmatrix}5\\0\end{Bmatrix}=\begin{Bmatrix}-1\\3\end{Bmatrix}\\
H(\omega_2)=I-\frac{2}{\omega^T_2\omega_2}\omega_2\omega_2^T=\frac{1}{5}\begin{Bmatrix}4&3\\3&-4\end{Bmatrix}\\
H(\omega_2)A_2=(H(\omega_2)\tilde{a_1},H(\omega_2)\tilde{a_2})=\begin{Bmatrix}5&2\\0&-1\end{Bmatrix}\\
Q_2=
\begin{Bmatrix}
1&0&0\\
0&\frac{4}{5}&\frac{3}{5}\\
0&\frac{3}{5}&-\frac{4}{5}
\end{Bmatrix}
\]
则有:
\[(Q_2Q_1)A=
\begin{Bmatrix}
1&1&1\\0&5&2\\0&0&-1
\end{Bmatrix}
=R
\]
则:
\[Q^T=Q_2Q_1=
\begin{Bmatrix}
1&0&0\\
0&\frac{4}{5}&\frac{3}{5}\\
0&\frac{3}{5}&-\frac{4}{5}
\end{Bmatrix}
\begin{Bmatrix}
0&1&0\\1&0&0\\0&0&1
\end{Bmatrix}\\
Q=
\begin{Bmatrix}
0&\frac{4}{5}&\frac{3}{5}\\
1&0&0\\
0&\frac{3}{5}&-\frac{4}{5}
\end{Bmatrix}\\
A=QR=\begin{Bmatrix}0&4&1\\1&1&1\\0&3&2\end{Bmatrix}
=
\begin{Bmatrix}
0&\frac{4}{5}&\frac{3}{5}\\
1&0&0\\
0&\frac{3}{5}&-\frac{4}{5}
\end{Bmatrix}
\begin{Bmatrix}
1&1&1\\0&5&2\\0&0&-1
\end{Bmatrix}
\]
(2)
首先,取正交矩阵 \(Q_1=\begin{Bmatrix}0&0&1\\0&1&0\\1&0&0\end{Bmatrix}\),左乘 A,得:
\[Q_1A=
\begin{Bmatrix}
0&0&1\\0&1&0\\1&0&0
\end{Bmatrix}
\begin{Bmatrix}0&4\\0&0\\5&2\end{Bmatrix}
=
\begin{Bmatrix}5&2\\0&0\\0&4\end{Bmatrix}
\]
再取正交矩阵 \(Q_2=\begin{Bmatrix}1&0&0\\0&0&1\\0&1&0\end{Bmatrix}\),左乘 \(Q_1A\),得:
\[Q_2(Q_1A)=
\begin{Bmatrix}1&0&0\\0&0&1\\0&1&0\end{Bmatrix}
\begin{Bmatrix}5&2\\0&0\\0&4\end{Bmatrix}=
\begin{Bmatrix}5&2\\0&4\\0&0\end{Bmatrix}=
\begin{Bmatrix}R\\0\end{Bmatrix}
\]
令 \(Q^T=Q_2Q_1=\begin{Bmatrix}1&0&0\\0&0&1\\0&1&0\end{Bmatrix}\begin{Bmatrix}0&0&1\\0&1&0\\1&0&0\end{Bmatrix}=\begin{Bmatrix}0&0&1\\1&0&0\\0&1&0\end{Bmatrix}\),则:
\[Q=\begin{Bmatrix}0&1&0\\0&0&1\\1&0&0\end{Bmatrix}
\]
从而有:
\[A=QR=
\begin{Bmatrix}0&4\\0&0\\5&2\end{Bmatrix}
=\begin{Bmatrix}0&1&0\\0&0&1\\1&0&0\end{Bmatrix}\begin{Bmatrix}5&2\\0&4\\0&0\end{Bmatrix}
\]
2.2 特殊矩阵特征系统
schur 分解
设 \(A\in C^{n\times n}\),则存在酉阵 \(U\in C^{n\times n}\) 使得
\[A=URU^H
\]
其中 \(R\in C^{n\times n}\) 为上三角矩阵.
- Schur 定理还可以表示为:任意 n 阶方阵A酉相似于一个以其特征值为对角元的上三角矩阵 R;显然上述 A 酉相似于 R
- R 的对角元可以按任意给定的顺序排列,R 通常称为 A 的 Schur 标准型。特征值的计算一般必须采用迭代法,通常无法在有限步内准确地得到
- Schur 分解定理只能在复矩阵空间成立,这是由于实矩阵 A 的特征值可能是一个复数,因此即使矩阵 A 是实矩阵,一般地,Schur分解中的 U,R 可能是复的
- U 的列向量未必都是 A 的特征向量,尽管其第一列是 A 的特征向量
正规矩阵
设 \(A\in C^{n\times n}\),若 \(A^H=AA^H\),则称\(A\) 为正规矩阵。
常见的复情形:
- Hermite 阵:\(A^H=A\)
- 斜 Hermite 阵:\(A^H=-A\)
- 酉阵:\(A^HA=AA^H=I\)
常见的实情形:
- 实对称矩阵:\(A^T=A\)
- 实反对称矩阵:\(A^T=-A\)
- 正交矩阵:\(A^TA=AA^T=I\)
推论:
-
设 A 为 n 阶方阵,则 A 为正规矩阵的充分必要条件是存在 n 阶酉阵 U,使得
\[A=UDU^H
\]
其中 \(D\in C^{n\times n}\)为对角矩阵。且D的对角元为A的特征值,酉阵 U 列为矩阵 A 的特征值对应的特征向量。
-
设 A 为 n 阶方阵,则 A 为 Hermite 矩阵的充分必要条件是存在 n 阶酉阵 U,使得
\[A=UDU^H
\]
其中 \(D\in R^{n\times n}\) 为实对角矩阵。
-
设 A 为 n 阶方阵,则 A 为斜 Hermite 矩阵的充分必要条件是存在 n 阶酉阵 U,使得
\[A=UDU^H
\]
其中 \(D\) 为对角矩阵,且对角元为纯虚数。
-
设 A 为 n 阶方阵,则 A 为酉矩阵的充分必要条件是存在 n 阶酉阵 U,使得
\[A=UDU^H
\]
其中 \(D\in C^{n\times n}\)为对角矩阵,且其对角元的模均为 1。
矩阵的谱半径与矩阵范数的关系
定理:设 A 为 n 阶方阵,\(\epsilon > 0\),则在 \(C^{n\times n}\) 中存在一种矩阵范数 \(||\cdot||_M\)(依赖于矩阵 A 和常数 \(\epsilon\) ),满足 \(||I||_M=1\) ,并且
\[||A||_M\leq \rho(A)+\epsilon
\]
推论:
-
若 \(\rho (A)<1\),则存在范数 \(||\cdot||\),使得 \(||A||<1\)
-
\(tr(A)=\sum\limits^m_{k=1}a_{kk}\ \ \ \ \ \ ||A||^2_F=\sum\limits^M_{i=1}\sum\limits^n_{j=2}||a_{ij}||^2=tr(A^HA)\)
-
定理:设 A 为 n 阶方阵,则存在 n 阶酉阵 U 和 V,使得
\[||UA||_F=||AV||_F=||UAV||_F=||A||_F
\]
称之为 F-范数的酉不变性
-
Schur 不等式:\(\sum\limits^n_{i=1}|\lambda_i|^2\leq\sum\limits^n_{i=1}\sum\limits^n_{j=1}|a_{ij}|^2\)
其中 \(\lambda_i\) 为 \(A\) 的特征值,并且 Schur 不等式中等号成立的充分必要条件是 A 为正规矩阵
证:根据 Schur 定理,存在 n 阶酉阵 U 使得 \(A=URU^H\)
\[\sum\limits^n_{i=1}\sum\limits^n_{j=1}|a_{ij}|2=||A||^2_F=||URU^H||^2_F=||R||^2_F=\sum\limits^n_{i=1}\sum\limits^n_{j=i+1}|r_{ij}|^2\geq\sum\limits^n_{i=1}|r_{ii}|^2\sum\limits^n_{i=1}|\lambda_i|^2
\]
2.3 矩阵的 Jordan 分解介绍
代数重数与几何重数
代数重数:设 A 为 n 阶方阵,A 的特征多项式为
\[\det (\lambda I_n-A)=(\lambda-\lambda_1)^{m_1}(\lambda-\lambda_2)^{m_2}\cdots (\lambda-\lambda_s)^{m_s}
\]
其中 \(m_i(i=1,2,\cdots,s\)) 均为正整数,\(\sum\limits^s_{i=1}m_i=n,\lambda_1,\lambda_2,\lambda_2,\cdots,\lambda_s\) 为 A 的不同的特征值,称 \(m_i\) 为 \(\lambda_i\) 的代数重数。
几何重数:把与 \(\lambda_i\) 对应的线性无关的特征向量的个数,即子空间 \(N(\lambda_i I_n-A)\)(即 \((\lambda_i I_n-A)x=0\) 的解空间,称为 \(\lambda_i I_n-A\) 的零空间)的维数,称为 \(\lambda_i\) 的几何重数,记为 \(\alpha_i,\ \alpha_i=n-\mathrm{rank}(\lambda_i I_n-A)\)。
代数重数和集合重数的关系:设 A 为 n 阶方阵, \(\lambda_i\) 为其特征值,\(m_i\) 和 \(\alpha_i\) 分别为其代数重数和几何重数,则 \(m_i\geq \alpha_i\)。
* 例14
计算矩阵 \(A=\begin{Bmatrix}-3&-3&-1\\1&0&0\\0&1&0\end{Bmatrix}\) 的特征值的 \(m_i\) 和 \(\alpha_i\)。
解:
令
\[\det(\lambda I - A)=
\begin{vmatrix}
\lambda +3&3&1\\
-1& \lambda&0\\
0&-1&\lambda
\end{vmatrix}
=(\lambda+1)^3=0
\]
故 A 的特征值为:\(\lambda_1=-1\) (三重根),从而 \(m_1=3\),而
\[\det(\lambda_1 I - A)=
\begin{vmatrix}
-1 +3&3&1\\
-1& -1&0\\
0&-1&-1
\end{vmatrix}
=
\begin{vmatrix}
2&3&1\\
-1& -1&0\\
0&-1&-1
\end{vmatrix}
=0
\]
显然 \(\begin{vmatrix}2&3\\ -1&-1\end{vmatrix}=1\neq0\),故 \(\mathrm{rank}(\lambda_1I - A)=2\),从而 \(\alpha_1=3-2=1<3=m_1\)
半单和亏损
定义:设 A 为 n 阶方阵,\(\lambda_i\) 为其特征值,\(m_i\) 和 \(\alpha_i\) 分别为其代数重数和几何重数,如果 \(m_i=\alpha_i\) ,则称特征值 \(\lambda_i\) 为半单的;如果 \(m_i>\alpha_i\) ,则称特征值 \(\lambda_i\) 为亏损的。
- 代数重数为 1 的特征值一定是半单的
- 不同特征值对应的特征向量是线性无关的
- 每个特征值都是半单的矩阵(酉完备的特征向量系)等价于可对角化
- 存在亏损的特征值的矩阵称为亏损矩阵等价于不可对角化
* 例15
下列矩阵是否可以相似对角化
\[A
\begin{Bmatrix}
-5&6&-3\\
-1&0&1\\
1&2&-1
\end{Bmatrix}
\ \
B=
\begin{Bmatrix}
1&-1&2\\
3&-3&6\\
2&-2&4
\end{Bmatrix}
\ \
C=
\begin{Bmatrix}
17&0&-25\\
0&3&0\\
9&0&-13
\end{Bmatrix}
\]
-
\[ \det(\lambda I_3-A)=(\lambda-2)(\lambda^2-2\lambda-2)
\ \
\lambda_1=2,\lambda_2=a+\sqrt{3},
\lambda_3=1-\sqrt{3}
\]
A 有三个不同的特征值,其必然可对角化
-
\[ \det(\lambda I_3-B)=\lambda^2(\lambda-2)\ \
\lambda_1=0,m_1=2;\lambda_2=2,m_2=1
\\
\mathrm{rank}(\lambda_1 I_3-B)=\mathrm{rank}(B)=1,\ \ 几何重数 \ \
\alpha_1=3-1=2\ \
\lambda_1 \ \ 是半单的
\]
B 可对角化
-
\[ \det(\lambda I_3-C)=(\lambda-2)^2(\lambda-3)\ \ \lambda_1=2,m_1=2;\lambda_2=3,m_1=1)\\
\mathrm{rank}(\lambda_1I_3-C)=2,\ \
几何重数 \ \
\alpha_1=3-2=1\ \
\lambda_1\ 是亏损的
\]
C 为亏损矩阵,不可对角化
矩阵的 Jordan 标准型
Jordan 块定义:称下面的 \(k\times k\) 阶方阵为 Jordan 块
\[J_k(\lambda)=
\begin{Bmatrix}
\lambda&1&&&&&\\
&\lambda&1&&&&\\
&&\ddots&\ddots&&\\
&&&&\lambda&1\\
&&&&&\lambda
\end{Bmatrix}
\]
例如:
\[J_4(0)=
\begin{Bmatrix}
0&1&&\\
&0&1&\\
&&0&1\\
&&&0
\end{Bmatrix}
\ \
J_3(2)=
\begin{Bmatrix}
2&1&\\
&2&1\\
&&2
\end{Bmatrix}
\ \
J_2(1)=
\begin{Bmatrix}
1&1\\
&1
\end{Bmatrix}
\]
Jordan 阵定义:由若干个 Jordan 块排成的块对角矩阵为 Jordan 阵。
例如:
\[J=
\begin{Bmatrix}
J_3(2)&&\\
&J_4(0)&\\
&&J_2(1)
\end{Bmatrix}
=\mathrm{diag}(J_3(2),J_4(0),J_2(1))
\]
定理:设 A 为 n 阶方阵,则存在 n 阶可逆矩阵 T 使得 \(A=TJT^{-1}\),其中
\[J=diag(J_{n_1}(\lambda_1),J_{n_2}(\lambda_2),\cdots,J_{n_k}(\lambda_k)),n_1+n_2+\cdots +n_k=n
\]
称上式为 A 的 Jordan 分解,J 称为 A 的 Jordan 标准型, T 称为变换矩阵;若不计 Jordan 块的次序,则Jordan 标准型唯一。
注:因为相似矩阵具有相同的特征值。所以 Jordan 标准型的对角元素 \(\lambda_1,\lambda_2,\cdots,\lambda_s\) 就是 A 的特征值。需要注意的是,在 Jordan 标准型 J 中,不同的 Jordan 块的对角元素 \(\lambda_i\) 可能相同,因此,\(\lambda_i\) 不一定是 A 的 \(n_i\) 重特征值,一般的,特征值 \(\lambda_i\) 的重数 大于或等于\(n_i\)。
* 例16
在有 8 个 Jordan 块的 11 阶 Jordan 标准型中:
\[\begin{Bmatrix}
0&&&&&&&&&&\\
&0&&&&&&&&&\\
&&0&&&&&&&&\\
&&&0&&&&&&&\\
&&&&-3&&&&&&\\
&&&&&2&&&&&\\
&&&&&&2&1&&&\\
&&&&&&&2&&&\\
&&&&&&&&2&1&\\
&&&&&&&&&2&1\\
&&&&&&&&&&2\\
\end{Bmatrix}
\]
有:
\[J_{n_1}(0)\ \
J_{n_2}(0)\ \
J_{n_3}(0)\ \
J_{n_4}(0)\ \
J_{n_5}(-3)\ \
J_{n_6}(2)\ \
J_{n_7}(2)\ \
J_{n_8}(2)
\]
\[\lambda=0 的重数 =n_1+n_2+n_3+n_4=4\\
\lambda=-3 的重数 =n_5=1\\
\lambda=2 的重数 =n_6+n_7+n_8=1+2+3=6
\]
Jordan 标准型相关:
- Jordan 标准型是一个块对角矩阵,对角元是矩阵 A 的特征值。
- 对于特征值 \(\lambda_i\),它的代数重数是 Jordan 标准型中以 \(\lambda_i\) 为特征值的 Jordan 块的阶数之和,不同 Jordan 块的特征值可能相同。
- 对于特征值 \(\lambda_i\),它的几何重数,即与 \(\lambda_i\) 对应的线性无关的特征向量的个数,恰以 \(\lambda_i\) 为特征值的 Jordan 块的个数。
定理 2.1.1
定理:设 A 为 n 阶方阵,\(\lambda_i\) 为其特征值,则 A 的 Jordan 标准型 J 中以 \(\lambda_i\) 为特征值,阶数为 \(l\) 的 Jordan 块的个数为:
\[r_{l+1}+r_{l-1}-2r_l
\]
其中,
\[r_l=rank(\lambda_iI-A)^l.\ r_0=rank(\lambda_iI-A)^0=rank(I)=n
\]
* 例17
求下列矩阵的 Jordan 标准型,其中
\[A=\begin{Bmatrix}3&0&8\\3&-1&6\\ -2&0&-5\end{Bmatrix}
\ \ \
B=\begin{Bmatrix}2&0&-1&0\\ -1&1&0&-1\\0&0&2&0\\1&1&1&3\end{Bmatrix}
\ \ \
C=\begin{Bmatrix}3&1&0&0\\ -4&-1&0&0\\0&0&2&1\\0&0&-1&0\end{Bmatrix}
\ \ \
D=\begin{Bmatrix}1&0&0&1\\1&1&0&2\\0&0&1&3\\0&0&0&2\end{Bmatrix}
\ \ \
\]
解:
-
对 \(A=\begin{Bmatrix}3&0&8\\3&-1&6\\ -2&0&-5\end{Bmatrix}\) 有
\[\det(\lambda I-A)=(\lambda+1)^3
\]
于是,A 的特征值为 \(\lambda_1=-1\),代数重数为 3,故以 \(\lambda_1=-1\) 为特征值的 Jordan 块阶数的和为 3,而
\[(\lambda_1I-1)=
\begin{Bmatrix}
-4&0&-8\\ -3&0&-6\\2&0&4
\end{Bmatrix}
\]
的任何二阶行列式的值均为 0,即 \(rank(\lambda_1I-A)=1,\ \ 3-rank(\lambda_1I-A)=2\)
故 \(\lambda_1=-1\) 的几何重数为 2,以 \(\lambda_1=-1\) 为特征值的 Jordan 块的个数为 2 个,因此 A 的 Jordan 标准型为
\[J=\begin{Bmatrix}-1&&\\&-1&1\\&&-1\end{Bmatrix}\ 或\ J=\begin{Bmatrix}-1&1&\\&-1&\\&&-1\end{Bmatrix}
\]
-
对 \(B=\begin{Bmatrix}2&0&-1&0\\ -1&1&0&-1\\0&0&2&0\\1&1&1&3\end{Bmatrix}\) 有
\[\det(\lambda I -B)=(\lambda-2)^4\\
\lambda_1=\lambda_2=\lambda_3=\lambda_4=2
\]
所以,B 的特征值为 \(\lambda_1=2\),代数重数为 4,以 2 为特征值的 Jordan 块的阶数之和为 4,且有
\[\mathrm{rank}(2I-B)=2\\
4-\mathrm{rank}(2I-B)=2\\
\]
故 \(\lambda=2\) 的几何重数为 2,以 \(\lambda=2\) 的特征值的 Jordan 块的个数为 2 个。所以,B 的 Jordan 标准型可能有两种形式如下:
\[J=
\begin{Bmatrix}
2&1&&\\
&2&&\\
&&2&1\\
&&&2
\end{Bmatrix}
\ 或\
J=
\begin{Bmatrix}
2&&&\\
&2&1&\\
&&2&1\\
&&&2
\end{Bmatrix}
\]
分别是 (2,2) 结构或 (1,3) 结构,
依据上述确定不同阶数的 Jordan 块的个数的定理,可以继续进行如下讨论,
(1)若 \(l=1\) ,则有
\[r_1=\mathrm{rank}(\lambda_1I-B)=\mathrm{rank}(2I-B)=2\\
(2I-B)^2=
\begin{Bmatrix}
0&0&1&0\\
1&1&0&1\\
0&0&0&0\\
-1&-1&-1&-1
\end{Bmatrix}^2
=
\begin{Bmatrix}
0&0&0&0\\
0&0&0&0\\
0&0&0&0\\
0&0&0&0
\end{Bmatrix}\\
r_2=\mathrm{rank}(\lambda_1I-B)^2=\mathrm{rank}(2I-B)^2=0
\]
可以确定以 2 为特征值,阶数为 1 的Jordan 块的个数为:
\[r_2+r_0-2r_1=0+4-2\times2=0
\]
显然,由于不存在 1 阶的 Jordan 块,因此 B 的 Jordan 标准型只能是 (2,2) 的结构。
(2)若 \(l=2\) ,则有
\[r_3=\mathrm{rank}(\lambda_1I-B)^3=\mathrm{rank}(2I-B)^3=0
\]
可以确定以 2 为特征值,阶数为 2 的Jordan 块的个数为:
\[r_3+r_1-2r_2=0+2-2\times0=2
\]
因此,存在两个阶数为 2 的 Jordan 块,所以 B 的 Jordan 标准型为(2,2)结构,具体表示如下:
\[J=
\begin{Bmatrix}
2&1&&\\
&2&&\\
&&2&1\\
&&&2
\end{Bmatrix}
\]
-
对 \(C=\begin{Bmatrix}3&1&0&0\\ -4&-1&0&0\\0&0&2&1\\0&0&-1&0\end{Bmatrix}\) 有
将 C 写成分块的形式,\(C=\begin{Bmatrix}C_1&\\&C_2\end{Bmatrix}\),其中
\[C_1=
\begin{Bmatrix}
3&1\\ -4&-1
\end{Bmatrix}
,\
C_2=
\begin{Bmatrix}
2&1\\ -1&0
\end{Bmatrix}
\]
分别求出子矩阵 \(C_1,\ C_2\) 的 Jordan 标准型,有
\[\det(\lambda I-C_1)=(\lambda-1)^2
\]
于是 \(C_1\) 的特征值为 \(\lambda=1\),且其代数重数为 2,又有 \(\lambda=1\) 的几何重数为 \(2-\mathrm{rank}(\lambda I-C_1)=2-1=1\),即 \(C_1\) 不可对角化,易得 \(C_1\) 的 Jordan 标准型为 \(J_1=\begin{Bmatrix}1&1\\0&1\end{Bmatrix}\)
再有
\[\det(\lambda I-C_2)=(\lambda-1)^2
\]
于是 \(C_2\) 的特征值为 \(\lambda=1\),代数重数为 2,有显然 \(\lambda=1\) 的几何重数为 \(2-\mathrm{rank}(\lambda I-C_2)=2-1\),即 \(C_2\) 不可对角化,易得 \(C_2\) 的 Jordan 标准型为 \(J_2=\begin{Bmatrix}1&1\\0&1\end{Bmatrix}\)。于是得到 C 的 Jordan 标准型为:
\[J=
\begin{Bmatrix}
J_1&\\&J_2
\end{Bmatrix}
=
\begin{Bmatrix}
1&1&0&0\\
0&1&0&0\\
0&0&1&1\\
0&0&0&1
\end{Bmatrix}
\]
-
对 \(D=\begin{Bmatrix}1&0&0&1\\1&1&0&2\\0&0&1&3\\0&0&0&2\end{Bmatrix}\) 有
\[\det(\lambda I -D)=(\lambda-2)(\lambda-1)^3=0
\]
可知,\(\lambda_1=1\)(三重),其代数重数 \(m_1=3\);
\(\lambda_2=2\) 其代数重数为 \(m_2=1\),是半单的。
对 \(\lambda_1=1\) 继续讨论,可得
\[\mathrm{rank}(\lambda_1I-D)=\mathrm{rank}(I-D)=2\\
4-\mathrm{rank}(\lambda_1-D)=2
\]
因此,其几何重数为 2,有两个对应的 Jordan 块,且各个 Jordan 阶数之和为 3;所以,只能是(1,2) 结构或 (2,1) 结构;可得 D 的 Jordan 标准型的一种可能表示如下所示:
\[J=
\begin{Bmatrix}
1&1&&\\
&1&&\\
&&1&\\
&&&2
\end{Bmatrix}
\]
关于变换矩阵 T
在求出 A 的 Joedan 标准型后,可以求相应的变换矩阵。依据 \(A=TJT^{-1}\) 或 \(AT=TJ\),将 T 按 J 的对角线上的 Jordan 块相应分块为
\[T=(T_1,T_2,\cdots,T_k)
\]
其中 \(T_i\) 是 \(n\times n\) 型矩阵,则有:
\[A(T_1,T_2,\cdots,T_k)=(T_1,T_2,\cdots,T_k)
\begin{Bmatrix}
J_{n_1}(\lambda_1)&&&\\
&J_{n_2}(\lambda_2)&&\\
&&\ddots&\\
&&&J_{n_k}(\lambda_k)
\end{Bmatrix}
\]
显然 \(\lambda_1,\lambda_2,\cdots,\lambda_k\),中可能有相同的,注意到
\[AT_i=T_iJ_{n_i}(\lambda_i)
\]
如果记 \(T_i=(t^i_1,t^i_2,\cdots,t^i_{n_i})\) ,于是可以得到
\[A(t^i_1,t^i_2,\cdots,t^i_{n_i})=(t^i_1,t^i_2,\cdots,t^i_{n_i})
\begin{Bmatrix}
\lambda_i&1&&\\
&\lambda_i&\ddots&\\
&&\ddots&1\\
&&&\lambda_i
\end{Bmatrix}
\]
\[\left\{
\begin{array}{lc}
At_1^i=\lambda_it_1^i\\
At_2^i=\lambda_it_2^i+t_1^i\ ,&t_i^j\in C^n\ ,&i=1,2,\cdots,k\ ;&j=1,2,\cdots,n_i\ ;\\
\vdots\\
At_{n_i}^i=\lambda_it_{n_i}^i+t_{n_i-1}^i
\end{array}
\right.
\]
称向量组 \(t_1^i,t^i_2,\cdots,t^i_{n_i}\) 为关于特征值 \(\lambda_i\) 的长度为 \(n_i\) 的 Jordan 链。
显然,该 Jordan 链的第一个向量就是矩阵 A 的关于特征值 \(\lambda_i\) 的特征向量,称其为链首,而链中的第 j 个向量可由等价的如下方程确定:
\[(A-\lambda_iI_n)t^i_j=t^i_{j-1},\ j=2,3,\cdots,n_i
\]
需要注意的是:
- Jordan 链的链首 \(t_1^i\) 不仅要求是一个特征向量,而且还要求可以利用上式求出 Jordan 链中的其他向量 \(t_2^i,\cdots,t^i_{n_i}\),也就是说不是任何一个特征向量都可以作为 Jordan 链的链首,链首要求是特征向量且方程组可解。
- 对应于某个特征值 \(\lambda_i\) 的 Jordan 链虽然一定存在,但当与 \(\lambda_i\) 相对应的线性无关的特征向量的个数大于或等于 2 时,关于特征 \(\lambda_i\) 值的那些特征向量中的任何一个有可能都不能作为链首,因此必须从 \(\lambda_i\) 的特征子空间中选取合适的向量作为 Jordan 链的链首,也就是对应特征向量空间中所有特征向量的某种线性组合。
* 例18
计算 *例17 中将 \(A=\begin{Bmatrix}3&0&8\\3&-1&6\\ -2&0&-5\end{Bmatrix}\) 化成 Jordan 标准型的变换矩阵 T
解:
由于已知
\[J=
\begin{Bmatrix}
J_1(\lambda_1)_{1\times1}&\\
&J_2(\lambda_2)_{2\times2}
\end{Bmatrix}
=
\begin{Bmatrix}
J_1(-1)_{1\times1}&\\
&J_2(-1)_{2\times2}
\end{Bmatrix}
=
\begin{Bmatrix}-1&&\\&-1&1\\&&-1\end{Bmatrix}
\]
则可得
\[AT=TJ\\
A(T_1T_2)=(T_1T_2)
\begin{Bmatrix}
-1&&\\
&-1&1\\
&&-1
\end{Bmatrix}
\]
令(上标用于区分特征值,对应于特征值的下标) \(T_1=t^1\in R^3,T_2=(t_1^2,t_2^2)\in R^{3\times2}\)
首先求出 \(\lambda_1=-1\) 所对应的线性无关的特征向量,其 Jordan 链的长度为 1,即 \(At^1=-t^1\),也就是
\[At^1=-t^1\\
(A+I)t^1=0\Leftrightarrow
\begin{Bmatrix}
4&0&8\\
3&0&6\\
-2&0&-4
\end{Bmatrix}
\begin{Bmatrix}
x_1\\x_2\\x_3
\end{Bmatrix}
=0
\Leftrightarrow
\left\{
\begin{array}{lc}
x_1+2x_3=0\\
x_1+2x_3=0\\
x_1+2x_3=0
\end{array}
\right.
\]
解得,线性无关的向量为:
\[t^1_{1}=
\begin{Bmatrix}
2\\0\\ -1
\end{Bmatrix}
\ \
t^1_{2}=
\begin{Bmatrix}
0\\1\\0
\end{Bmatrix}
\]
这样就可以任取其一作为以 \(\lambda_1=-1\) 长度为 1 的 Jordan 链的链首和链尾,即
\[T_1=t_1^1 \ 或 \ T_1=t_2^1
\]
接下来确定 \(\lambda_2=-1\) 长度为 2 的 Jordan 链的链首,可得:
\[A(t_1^2t_2^2)=(t_1^2t_2^2)
\begin{Bmatrix}
-1&1\\&-1
\end{Bmatrix}
=
(-t^1_2,t_1^2-t_2^2)
\]
类似的,与 \(\lambda_1=-1\) 的特征向量一致,解出 \(\lambda_2=-1\) 线性无关的特征向量为:
\[At^2_1=-t^2_1\\
(A+I)t^2=0\Leftrightarrow
\begin{Bmatrix}
4&0&8\\
3&0&6\\
-2&0&-4
\end{Bmatrix}
\begin{Bmatrix}
x_1\\x_2\\x_3
\end{Bmatrix}
=0
\Leftrightarrow
\left\{
\begin{array}{lc}
x_1+2x_3=0\\
x_1+2x_3=0\\
x_1+2x_3=0
\end{array}
\right.
\\
t^2_{11}=
\begin{Bmatrix}
2\\0\\ -1
\end{Bmatrix}
\ \
t^2_{12}=
\begin{Bmatrix}
0\\1\\0
\end{Bmatrix}
\]
验证可得,以 \(t^2_{11}\) 或 \(t^2_{12}\) 为链首均无法求出另一个向量构造 Jordan 链,即:
\[(-I-A)x=t_{11}^2\Leftrightarrow
\left\{
\begin{array}{lc}
x_1+2x_3=0\\
x_1+2x_3=1\\
x_1+2x_3=0
\end{array}
\right.
\ \ ,\ 无解\ ;
\\
(-I-A)x=t_{12}^2\Leftrightarrow
\left\{
\begin{array}{lc}
x_1+2x_3=2\\
x_1+2x_3=0\\
x_1+2x_3=-1
\end{array}
\right.
\ \ ,\ 无解\ ;
\]
所以,利用特征向量的线性组合,求出 \(y\in span\{t^2_{11},t^2_{12}\}\),使得 \((A-\lambda_1I)z=y\) 有解。令 \(y=k_1t^2_{11}+k_2t^2_{12}\) 可得
\[(A-\lambda_1I|y)=(A+I|y)=
\begin{Bmatrix}
4&0&8&2k_1\\
3&0&6&k_2\\
-2&0&-4&-k_1
\end{Bmatrix}
\rightarrow
\begin{Bmatrix}
1&0&2&\frac{k_1}{2}\\
0&0&0&-\frac{k_1}{2}+\frac{k_2}{3}\\
0&0&0&0
\end{Bmatrix}
\]
由于 \((A-\lambda_1I)z=y\) 有非零解,必须满足 \(3k_1=2k_2\),从而解出 \(k_1=2,k_2=3\),得到 \(y=(4,3,-2)^T\) 作为链首,并且
\[(A+I|y)\rightarrow
\begin{Bmatrix}
1&0&2&1\\
0&0&0&0\\
0&0&0&0
\end{Bmatrix}
\]
可以得到链尾 \(z=(0,0,-0)^T\)
所以可以得出变换矩阵 T 为
\[T=(T_1,T_2),T_1=t^1_1=
\begin{Bmatrix}
2\\0\\ -1
\end{Bmatrix}
,\ \
T_2=(y,z)
=
\begin{Bmatrix}
4&1\\3&0\\ -2&0
\end{Bmatrix}
\]
或
\[T=(T_1,T_2),T_1=t^1_2=
\begin{Bmatrix}
0\\1\\0
\end{Bmatrix}
,\ \
T_2=(y,z)
=
\begin{Bmatrix}
4&1\\3&0\\ -2&0
\end{Bmatrix}
\]
变换矩阵也就可以表示为
\[T=
\begin{Bmatrix}
2&4&1\\0&3&0\\ -1&-2&0
\end{Bmatrix},\
T^{-1}=
\begin{Bmatrix}
0&-\frac{2}{3}&-1\\
0&\frac{1}{3}&0\\
1&0&2
\end{Bmatrix}
\]
或
\[T=
\begin{Bmatrix}
0&4&1\\1&3&0\\0&-2&0
\end{Bmatrix},\
T^{-1}=
\begin{Bmatrix}
0&1&\frac{3}{2}\\
0&0&-\frac{1}{2}\\
1&0&2
\end{Bmatrix}
\]
矩阵的 Jordan 分解
Jordan 标准型 J:
- 计算矩阵的全部特征值
- 计算特征值的代数重数(确定对角元)
- 计算特征值的几何重数(Jordan 块个数)
- 利用定理 2.1.1 确定每个 k 阶块的个数(为节省计算量从小到大计算)
变换矩阵 T
- 求得 Jordan 标准型
- 计算每个 Jordan 块对应的 Jordan 链
- 若 Jordan 块阶数为 1,直接计算特征向量
- 若阶数大于 1,则先计算特征向量,利用特征向量的线性组合得到链首
应用
- 计算初等函数在某个矩阵处的值(矩阵)
- (高次)多项式函数
- Hamilton-Caylay 定理
Hamilton-Caylay 定理
定理:设 \(A\in C^{n\times n},\psi(\lambda)=\det (\lambda I-A)\),则 \(\psi(A)=O\)
* 例19
已知矩阵 \(A=\begin{Bmatrix}-1&1&0\\ -4&3&0\\1&0&2\end{Bmatrix}\),计算
-
\(A^7-A^5-19A^4+28A^3+6A-4I\)
-
\(A^{-1}\)
-
\(A^{100}\)
解:
\(\psi(\lambda)=\det(\lambda I-A)=\lambda^3-4\lambda^2+5\lambda-2\)
(1)
令
\[f(\lambda)=\lambda^7-\lambda^5-19\lambda^4+28\lambda^3+6\lambda-4
\]
利用多项式除法
\[\begin{equation}
\begin{aligned}
f(\lambda)&=a(\lambda)\psi(\lambda)+b(\lambda)\\
&=(\lambda^4+4\lambda^3+10\lambda^2+3\lambda-2)\psi(\lambda)-3\lambda^2+22\lambda-8
\end{aligned}
\end{equation}
\]
所以
\[f(A)=-3A^2+22A-8I=
\begin{Bmatrix}
-19&6&0\\
-64&43&0\\
19&-3&24
\end{Bmatrix}
\]
(2)
显然有:
\[\psi(A)=A^3-4A^2+5A-2I=O\\
I=A(\frac{1}{2}(A^2-4A+5I))\\
A^{-1}=\frac{1}{2}(A^2-4A+5I)=
\begin{Bmatrix}
3&-1&0\\
4&-1&0\\
-\frac{3}{4}&\frac{1}{2}&\frac{1}{2}
\end{Bmatrix}
\]
(3)
显然有
\[\psi(\lambda)=(\lambda-2)(\lambda-1)^2
\\
\psi(2)=\psi(1)=\psi'(1)=0
\]
利用多项式除法,并且带入已知值确定余项的系数,得到
\[\lambda^{100}=g(\lambda)\psi(\lambda)+a\lambda^2+b\lambda+c\\
\left\{
\begin{array}{lm}
a^{100}=4a+2b+c\\
1=a+b+c\\
100=2a+b
\end{array}
\right.
\Rightarrow
\left\{
\begin{array}{lm}
a=2^100-101\\
b=-2^{101}+302\\
c=2^{100}-200
\end{array}
\right.
\]
所以有:
\[\begin{aligned}
A^{100}&=g(A)\psi(A)+aA^2+bA+cI\\
&=aA^2+bA+cI\\
&=
\begin{Bmatrix}
-199&100&0\\
-400&201&0\\
201-2^{100}&2^{100}-101&2^{100}
\end{Bmatrix}
\end{aligned}
\]
2.4 矩阵奇异值分解
奇异值定义:设 \(A\in C^{m\times n},k=\min(m,n)\),Hermite 半正定矩阵 \(A^HA\) 的特征值为
\[\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_k\geq0
\]
称非负实数
\[\sigma_i(A)=\sqrt{\lambda_i},i=1,2,\cdots,k
\]
为矩阵 A 的奇异值.
定理 (奇异值酉不变性):设 \(A,B\in C^{m\times n}\),如果存在 m 阶、n 阶酉阵 U、V,使得 \(A=UBV^H\),则矩阵 A、B 的奇异值相同
奇异值分解定理:设 \(A\in C^{m\times n}\) ,且 \(\mathrm{rank}(A)=r\),则存在 m 阶、n 阶酉阵 U、V,使得
\[A=U\begin{Bmatrix}
\Sigma&0\\0&0
\end{Bmatrix}
V^H
\]
上式称为 A 的满的奇异值分解,其中 \(\Sigma=\mathrm{diag}(\sigma_1,\cdots,\sigma_r),\sigma_i\neq0,(i=1,2,\cdots,r)\)(diag 表示对角阵),非负实数 \(\sigma_i\) 称为矩阵 A 的非零奇异值。
奇异值分解亦可写为:
\[A=U\begin{Bmatrix}
\Sigma&0\\0&0
\end{Bmatrix}
V^H=(U_1,U_2)
\begin{Bmatrix}
\Sigma&0\\0&0
\end{Bmatrix}
\begin{Bmatrix}
V_1^H\\V_2^H
\end{Bmatrix}
=U_1\Sigma V_1^H
\\
A=U_1\Sigma V_1^H
\]
上式称为 A 的约化的奇异值分解,与满的奇异值分解相对应
左右奇异向量:
长方阵的奇异值、左右奇异向量与方阵的特征值、左右特征向量想对应。
\[A=U_1\Sigma V_1^H\Rightarrow U_1^HA=\Sigma V_1^H,u^H_iA=\sigma_i v_i^H,i=1,2,\cdots,r
\]
U 的列向量 \(u_1,u_2,\cdots,u_m\),称为矩阵 A 的与奇异值 \(\sigma_i\) 对应的左奇异向量
\[A=U_1\Sigma V_1^H\Rightarrow AV_1=U_1\Sigma,Av_i=\sigma_iu_i,i=1,2,\cdots,r
\]
V 的列向量 \(v_1,v_2,\cdots,v_n\),称为矩阵 A 的与奇异值 \(\sigma_i\) 对应的右奇异向量。且有:
\[AA^HU=U
\begin{Bmatrix}
\Sigma&0\\0&0
\end{Bmatrix}
V^HV
\begin{Bmatrix}
\Sigma&0\\0&0
\end{Bmatrix}
U^HU=
U
\begin{Bmatrix}
\Sigma^2&0\\0&0
\end{Bmatrix}\\
A^HAV=V
\begin{Bmatrix}
\Sigma&0\\0&0
\end{Bmatrix}
U^HU
\begin{Bmatrix}
\Sigma&0\\0&0
\end{Bmatrix}
V^HV
=
V
\begin{Bmatrix}
\Sigma^2&0\\0&0
\end{Bmatrix}
\]
左奇异向量 \(u_1,u_2,\cdots,u_m\) 为 \(AA^H\) 的单位正交特征向量
右奇异向量 \(v_1,v_2,\cdots,v_n\) 为 \(A^HA\) 的单位正交特征向量
推论:
设 \(A\in C^{n\times n}\) ,且 \(\mathrm{rank}(A)=n\),则存在 n 阶酉阵 U、V,使得
\[A=U\begin{Bmatrix}
\sigma_1&&&\\&\sigma_2&&\\&&\ddots&\\&&&\sigma_n
\end{Bmatrix}
V^H
\]
其中 \(\sigma_i>0,\;i=0,1,2,\cdots,n\) 称为矩阵 A 的奇异值。
SVD(奇异值分解)和特征值分解的不同:
- SVD 有左右两组不同的基,特征值分解分解只有特征向量一组
- SVD 使用正交基,而特征向量不一定正交
- 所有矩阵都有奇异值分解,而不是所有的矩阵(方阵)都有特征值分解
奇异值分解的步骤
针对矩阵 A:
-
利用 Schur 分解得到 \(V^H(A^HA)V=\begin{Bmatrix}\Sigma^2&0\\0&0\end{Bmatrix}\),其中
\[\Sigma=
\begin{Bmatrix}
\sigma_1&&&\\
&\sigma2&&\\
&&\ddots\\&
&&&\sigma_r
\end{Bmatrix}
\]
,且 \(\sigma_i=\sqrt{\lambda_i},i=1,2,\cdots,r\)
-
将 V 矩阵分块:\(V=(V_1,V_2),V_1\in C^{n\times r,V_2\in C^{n\times (n-r)}}\);\(V_1\) 各列是非零特征值对应的特征向量,\(V_2\) 各列是零特征值对应的特征向量,\(AV1\) 的列相互正交;\(AV_2=0\)
-
令\(U_1=AV_1\Sigma^{-1}\in C^{m\times r}\),且满足 \(U^HU=I_r\)
-
再取 \(U_2\in C^{m\times(m-r)}\) 为 \(U_1\) 的标准正交补,即 \(U^H_2U_1=0\),做 \(U=(U_1,U_2)\in C^{m\times m},U^HU=I\)
-
满:\(A=U\begin{Bmatrix}\Sigma&0\\0&0\end{Bmatrix}V^H\)
约化:\(A=U_1\Sigma V^H_1\)
* 例20
求矩阵 \(A=\begin{Bmatrix}1&0&1\\0&1&1\\0&0&0\end{Bmatrix}\) 的奇异值分解
解:
求解次序为:\(\Sigma,V,V_1,U_1,U\)。计算矩阵
\[A^HA=
\begin{Bmatrix}
1&0&0\\0&1&0\\1&1&0
\end{Bmatrix}
\begin{Bmatrix}
1&0&1\\0&1&1\\0&0&0
\end{Bmatrix}
=
\begin{Bmatrix}
1&0&1\\0&1&1\\1&1&2
\end{Bmatrix}
\]
令 \(\det(\lambda I-A^HA)=\lambda(\lambda-1)(\lambda-3)=0\)
则 \(A^HA\) 的特征值和 A 的奇异值分别为:
\[\lambda_1=3,\lambda_2=1,\lambda_3=0;\\
\sigma_1=\sqrt{3},\sigma_2=1,\sigma_3=0
\]
所以 \(\Sigma=\begin{Bmatrix}\sqrt{3}&0\\0&1\end{Bmatrix}\)
求出特征向量并使其标准正交化,得到矩阵 V
\[\begin{Bmatrix}
2&0&-1\\0&2&-1\\ -1&-1&1
\end{Bmatrix}
\begin{Bmatrix}
x_1\\x_2\\x_3
\end{Bmatrix}
=\begin{Bmatrix}
0\\0\\0
\end{Bmatrix}
\ \ \ p_1=
\begin{Bmatrix}
1\\1\\2
\end{Bmatrix}
\ \
v_1=\frac{p_1}{||p_1||_2}=\frac{1}{\sqrt{6}}\begin{Bmatrix}
1\\1\\2
\end{Bmatrix}
\]
\[\begin{Bmatrix}
0&0&-1\\0&0&-1\\ -1&-1&-1
\end{Bmatrix}
\begin{Bmatrix}
x_1\\x_2\\x_3
\end{Bmatrix}
=
\begin{Bmatrix}
0\\0\\0
\end{Bmatrix}
\ \
p_2=
\begin{Bmatrix}
1\\ -1\\0
\end{Bmatrix}
\ \
v_2=\frac{p_2}{||p_2||_2}=\frac{1}{\sqrt{2}}
\begin{Bmatrix}
1\\ -1\\0
\end{Bmatrix}
\]
\[\begin{Bmatrix}
-1&0&-1\\0&-1&-1\\ -1&-1&-2
\end{Bmatrix}
\begin{Bmatrix}
x_1\\x_2\\x_3
\end{Bmatrix}
=
\begin{Bmatrix}
0\\0\\0
\end{Bmatrix}
\ \
p_3=
\begin{Bmatrix}
-1\\ -1\\1
\end{Bmatrix}
\ \
v_3=\frac{p_3}{||p_3||_2}=\frac{1}{\sqrt{3}}
\begin{Bmatrix}
-1\\ -1\\1
\end{Bmatrix}
\]
\[V=
\begin{Bmatrix}
\frac{1}{\sqrt{6}}&\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{3}}\\
\frac{1}{\sqrt{6}}&\frac{-1}{\sqrt{2}}&\frac{-1}{\sqrt{3}}\\
\frac{2}{\sqrt{6}}&0&\frac{1}{\sqrt{3}}
\end{Bmatrix}
\]
因 rank(A)=2,固有
\[V_1=
\begin{Bmatrix}
\frac{1}{\sqrt{6}}&\frac{1}{\sqrt{2}}\\
\frac{1}{\sqrt{6}}&\frac{-1}{\sqrt{2}}\\
\frac{2}{\sqrt{6}}&0
\end{Bmatrix}
\ \
U_1=AV_1\Sigma^{-1}=
\begin{Bmatrix}
1&0&1\\0&1&1\\0&0&0
\end{Bmatrix}
\begin{Bmatrix}
\frac{1}{\sqrt{6}}&\frac{1}{\sqrt{2}}\\
\frac{1}{\sqrt{6}}&\frac{-1}{\sqrt{2}}\\
\frac{2}{\sqrt{6}}&0
\end{Bmatrix}
\begin{Bmatrix}
\frac{1}{\sqrt{3}}&0\\0&1
\end{Bmatrix}
=
\begin{Bmatrix}
\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\
\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}\\
0&0
\end{Bmatrix}
\]
得到约化的奇异值分解
\[A=U_1\Sigma V_1^H=
\begin{Bmatrix}
\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\
\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}\\
0&0
\end{Bmatrix}
\begin{Bmatrix}
\sqrt{3}&0\\0&1
\end{Bmatrix}
\begin{Bmatrix}
\frac{1}{\sqrt{6}}&\frac{1}{\sqrt{6}}&\frac{2}{\sqrt{6}}\\
\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}&0
\end{Bmatrix}
\]
计算 \(U_2\),使其与 \(U_1\) 构成 \(R^3\) 的一组标准正交基,可取 \(U_2=\begin{Bmatrix}0\\0\\1\end{Bmatrix}\) 则
\[U=(U_1U_2)=
\begin{Bmatrix}
\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}&0\\
\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}&0\\
0&0&1
\end{Bmatrix}
\]
是酉阵,故矩阵 A 的奇异值分解(满的奇异值分解)为
\[A=
\begin{Bmatrix}
\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}&0\\
\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}&0\\
0&0&1
\end{Bmatrix}
\begin{Bmatrix}
\sqrt{3}&0&0\\0&1&0\\0&0&0
\end{Bmatrix}
\begin{Bmatrix}
\frac{1}{\sqrt{6}}&\frac{1}{\sqrt{6}}&\frac{2}{\sqrt{6}}\\
\frac{1}{\sqrt{2}}&\frac{-1}{\sqrt{2}}&0\\
\frac{-1}{\sqrt{3}}&\frac{-1}{\sqrt{3}}&\frac{1}{\sqrt{3}}
\end{Bmatrix}
\]
奇异值分解讨论矩阵的性质
-
像空间、零空间:
R(A) 为由 A 的列向量生成的子空间,称为 A 的值域或像空间,即:
\[R(A)=\mathrm{span}\{a_1,a_2,\cdots,a_n\}
\]
N(A) 称为 A 的零空间或核空间,即
\[\mathrm{N}(A)=\{x|Ax=0\}
\]
-
像空间、零空间基底:
\[R(A)=\mathrm{span}\{u_1,u_2,\cdots,u_n\},\
N(A)=\mathrm{span}\{v_{r+1},v_{r+2},\cdots,v_{r+n}\}
\]
其中 \(u_i\) 和 \(v_i\) 分别为矩阵 U 和 V 的正交向量
-
Hermite 矩阵的奇异值为其特征值的绝对值
\[A^H=A,\ \sigma(A)=\sqrt{\lambda(A^HA)}=\sqrt{\lambda(A^2)}=\sqrt{\lambda(A)^2}=|\lambda(A)|
\]
-
矩阵 A 的非零奇异值的个数恰为矩阵 A 的秩
\[\mathrm{rank}(A^HA)=\mathrm{rank}(AA^H)=\mathrm{rank}(A^H)=\mathrm{rank}(A)
\]
-
当 A 为非奇异矩阵时,有 \(||A^{-1}||_2=\frac{1}{\sigma_n}\),其中 \(\sigma_n\) 为 A 最小的奇异值
-
设 \(\sigma_1\geq\sigma_2\geq\cdots\geq\sigma_r>0\) 则
\[||A||_2=\sigma_1,\\
||A||_F=\sqrt{\mathrm{trace}(A^HA)}=\sqrt{\sigma_1^2+\sigma_2^2+\cdots+\sigma_r^2},\\
|\det(A)|=\prod\limits^n_{i=1}\sigma_i
\]
-
秩为 r 的 \(m\times n\) 阶矩阵 A 可以表示为 r 个秩为 1 的矩阵的和
\[A=
\sigma_1u_1v^H_1+
\sigma_2u_2v^H_2+\cdots+
\sigma_ru_rv^H_r
\]
矩阵奇异值分解的几何意义可以理解为将向量从单位圆投影到一个椭圆上?
在高维上,对应的是将向量从单位球拖影到一个超椭球上;
超椭球:将单位球某些正交方向分别以拉伸因子 \(\sigma_i\) 拉伸而成的曲面,\(u_i\) 为主半轴,\(\sigma_i\) 为主半轴的长度,恰好是矩阵的奇异值
* 例21
矩阵 A 的非零奇异值为 1,3,5
A 的秩为多少? 3
\(||A||_2,||A||_F,|\det(A)|\) 分别为多少?
\(||A||_2=5,||A||_F=\sqrt{35},|\det(A)|=15\)
特征系统分解总结
-
Schur 分解:\(A\in C^{n\times n},A=URU^H\),U 为酉矩阵,R 为上三角矩阵
-
Jordan 分解:\(A\in C^{n\times n},A=TJT^{-1}\),T 为可逆矩阵,J 为 A 的 Jordan 标准型
-
特征值分解:\(A\in C^{n\times n},A=TDT^{-1}\),A 非亏损,T 的列为 A 的特征值对应的特征向量
-
奇异值分解:\(A\in C^{m\times n},A=UDV^{H}\),U,V 为酉矩阵,D 为对角矩阵,D 的元素为 A 的奇异值
-
约化的奇异值分解:\(A=U_1\Sigma V_1^H\),\(\Sigma\) 为对角矩阵,\(\Sigma\) 的元素为 A 的非零奇异值。\(V_1\) 的列为 A 的非零奇异值对应的右奇异向量,\(U_1\) 的列为 A 的非零奇异值对应的左奇异向量。
-
END





 矩阵与数值分析第二章内容
矩阵与数值分析第二章内容

