Sub-graph Contrast for Scalable Self-Supervised Graph Representation Learning
Sub-graph Contrast for Scalable Self-Supervised Graph Representation Learning
动机
-
图表示学习最近引起了很多关注。由于有限的计算和内存成本,现有的以完整图数据为基础的图神经网络不可扩展。因此,在大规模图数据中捕获丰富的信息仍然是一个巨大的挑战
-
自监督学习为解决上述问题提供了潜在的解决方案。然而,现有的自监督工作也对完整的图数据进行操作,并且在定义基于互信息的损失项时偏向于拟合全局(
DGI)或仅限局部(1 跳邻域)(GMI)图结构
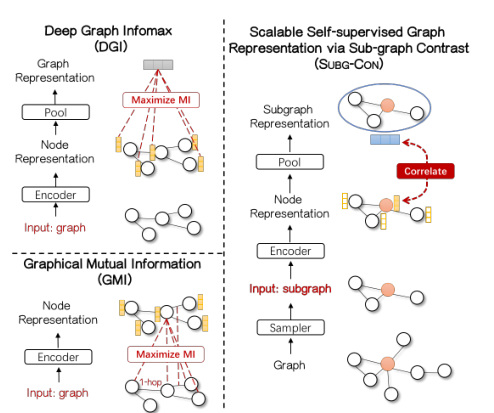
DGI 旨在训练一个节点编码器,使节点表示和池化全局图表示之间的互信息最大化
GMI 提出最大化每个节点的隐藏表示与其一跳邻居的原始特征之间的互信息。在定义基于互信息的损失项时,这些工作往往偏向于拟合整体或非常局部(1 跳邻居)图结构,这会损害学习表示的质量
贡献
- 通过子图对比提出了一种新颖的自监督图表示学习方法。它利用中心节点和上下文子图的相关性来捕获区域图结构信息
- 在图上引入了一种数据增强策略,旨在使用子图采样从现有图增加训练样本,以进行自监督图表示学习
- 通过使用小尺寸和简单结构的子图进行训练,
SUBG-CON方法需要更少的训练时间和计算内存成本来进行图表示学习 - 基于采样的子图实例,该方法支持并行图表示学习,以进一步提高效率和可扩展性
- 与之前在来自不同领域的多个真实世界图形数据集上的无监督和监督方法相比,大量实验验证了我们工作的有效性和效率
思想
框架
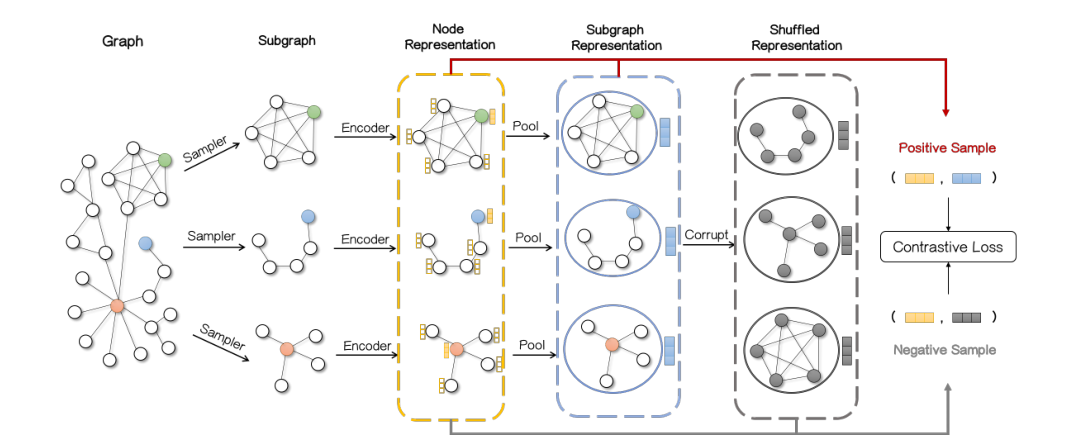
method
Subgraph Sampling Based Data Augmentation
对于数据增强,其主要是通过将原图进行一系列的采样得到不同的子图,对于一个中心节点 \(i\) ,其采样出的子图主要通过使用重要度分数 \(S\) 进行采样,其中重要度分数计算如下:
\[\mathbf{S}=\alpha \cdot(\mathbf{I}-(1-\alpha) \cdot \overline{\mathbf{A}})\\
\overline{\mathbf{A}} = \mathbf{A}\mathbf{D}^{-1}
\]
对于中心节点 \(i\) ,子图采样器 \(S\) 选择 topk 个重要邻居与得分矩阵 \(S\) 组成一个子图。所选节点的索引可以表示为:
\[idx=\text { top\_rank }(\mathbf{S}(i,:), k),
\]
那么子图的节点特征和对应的邻接矩阵:
\[\mathbf{X}_{i}=\mathbf{X}_{i d x,:}, \quad \mathbf{A}_{i}=\mathbf{A}_{i d x, i d x}
\]
Encoding Subgraph F or Representations
对于节点 \(i\) 上下文子图进行编码:
\[\mathbf{H}_{i}=\mathcal{E}\left(\mathbf{X}_{i}, \mathbf{A}_{i}\right)
\]
中心节点嵌入\(h_i\) 是从潜在表示矩阵\(H_i\)中选取的
\[h_i = \mathcal{C}(H_i)
\]
利用读取函数得到上下文子图的嵌入:
\[s_i = \mathcal{R}(H_i)
\]
Contrastive Learning via Central Node and Context Sub-graph
为了构造负例,通过函数 \(\mathcal{P}\) 对采样得到的一系列子图进行破坏生成相应负样例:
\[\left\{\widetilde{\mathbf{s}}_{1}, \widetilde{\mathbf{s}}_{2} \ldots, \widetilde{\mathbf{s}}_{M}\right\} \sim \mathcal{P}\left(\left\{\mathbf{s}_{1}, \mathbf{s}_{2}, \ldots, \mathbf{s}_{m}\right\}\right)
\]
最终的损失函数为:
\[\mathcal{L}=\frac{1}{M} \sum_{i=1}^{M} \mathbb{E}_{(\mathbf{X}, \mathbf{A})}\left(-\max \left(\sigma\left(\mathbf{h}_{i} \mathbf{s}_{i}\right)-\sigma\left(\mathbf{h}_{i} \widetilde{\mathbf{s}}_{i}\right)+\epsilon, 0\right)\right)
\]
code

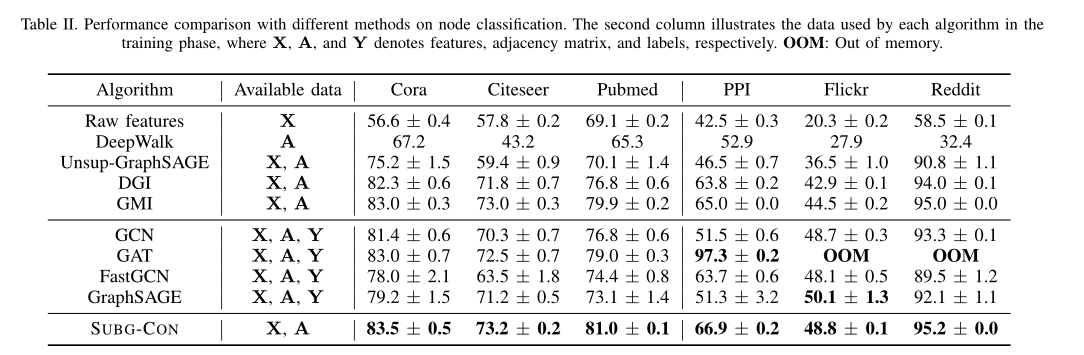
实验
结论
最大的创新是突出了子图和节点级别的对比

