自监督-Self-Supervised Graph Learning with-Proximity-based Views and Channel Contrast

动机

• 图神经网络使用邻域据级作为核心, 导致邻居节点之间的特征平滑, 虽然在个预测任务中取得成功, 但这种凡是无法扑获远距离节点的相似性, 而对于扑获远距离相似性对于高质量的学习非常重要.
• GNN 的假设是相似的节点应该有连接并且他们属于同一类的, 通过邻域据级进行局部特征平滑, 这些模型倾向于生成节点嵌入, 以保持原始图中节点的邻近性, 然而, 这些方法在一些现实中的网络面临挑战, 在现实网络中, 邻域不一定以为着相似性, 有时真正相似的节点相距甚远.

贡献

• 提出了特征&拓扑邻近保持图 FT-GCL, 一个基于临近保持图的无监督图表示学习(GRL)框架

思想

框架

在该框架中, 首先根据原图 \(G\) 中节点或结构相似度重新构造图 \(G_f, G_t\) , 然后随机使 \(G_a = G_f ~or~ G_{a} = G_{t}\), 然后将原图 \(G\) 和加强的图 \(G_a\) 同时喂入 GNNs 编码编码, 经过投影头 MLP, 最后用通道级对比正样本对和负样本对.

step-1: View generation

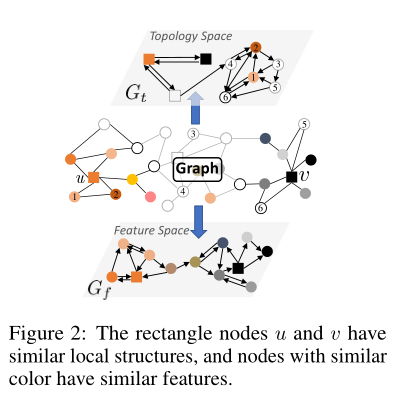
​ 我们首先为所有节点提取局部子图, 其中子图可以是 \(r-hop ~~ ego\) (即每个节点周围的生成子图) 或由从每个节点开始的一组随机游走序列生成的子图. 实际上, 不同的选择不会显著影响结果, 并且 RW(随机游走)对于密集图更有效. Let \(\mathcal{S} =\{S1,S2,...,S_N \}\) 是为每个节点提取的局部子图的集合, 我们采用了 Weisfeiler-Lehman (WL) 子树核, 具有固定的数量在子图 \(\mathcal{S}\) 上迭代. 最后可以得到一个对称的半正定核 \(K \in \mathbb{R}^{N \times N}\). 其中 \(K_{ij}\) 定义为局部子图 \(S_i\) 和 \(S_j\) 相似, 可以看作是 \(v_i\) 和 \(v_j\) 之间的局部拓扑相似性. 然后, 直接对 \(K\) 进行因式分解, 得到每个子图表示. 这导致较高的计算复杂性. 我们使用 Nystrom 方法去减少复杂性. Nyström 方法只使用了 \(K\) 中的 \(m\) 行的一个小子集, 因此 \(k≈RR^T\) 其中 \(R \in \mathbb{R}^{N \times m}\). 最后, \(R\) 的每一行表示对应节点在图的拓扑空间中的坐标, 因此作为节点的局部拓扑表示.

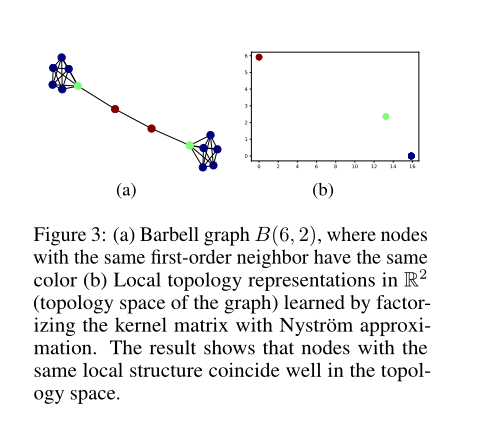
​ 上图显示了杠铃图, 在 \(a\) 中有相同的一阶邻居中颜色颜色相同时局部拓扑表示在 \(\mathbb{R}^2\) (图中的拓扑空间)上学习表示通过核矩阵因式分解方法在 \(b\) 表明，具有相同局部结构的节点在拓扑空间中具有良好的重合性.

​ 在特征空间中, 基于节点特征 \(X\) 由 \(G\) 生成的临近图 \(G_f\) . 两个临近图都是用余弦相似性作为距离的度量. 在视图生成阶段, 计算成本主要来自计算 \(kNN\) 图的向量相似度.两个图 \(G_f、G_t\) 和 \(k_f = k_t = k\) 被定义 \(\mathbb{P}(·|G, k)\). 在每个训练步骤中, 我们随机设置 \(k\) 值生成一个视图 \(G_a \sim \mathbb{P}(·|G, k)\)，其中 \(G_a\) 交替设置 \(G_f ~or~G_t\). 的随机性 \(k\) 有助于提高生成视图的多样性, 这样可以保留不同尺度的邻近性. 然而，在每个训练步骤中重复构造 \(kKK\) 图是昂贵的. 我们限制 \(k_f, k_t\) 的值在 \(k_{max}\) 之内, 即 \(k_f, k_t ≤ k_{max}\). 只需要在训练前在特征和拓扑空间中为每个节点找到\(top-k_{max}\) 邻居, 在每个训练步骤中, 在相似性排序结束时, 通过屏蔽一定数量的邻居, 可以很容易地从预处理后的 \(k_{max}\) 中获得 FPG \(k_f\) 和TPG \(k_t\). 在实践中, 手动将 \(k_{max}\) 设置为超参数, 并且 \(k_{max}<10\) 可以很好地工作.

Step-2: Shared GNN encoder

视图 \(G_a \sim \mathbb{P}(·|G, k)\) 和 \(G\) 一起喂进到 (Di)GNN 编码 GNN(A,X), 其中每个节点聚合从它的邻居传播的消息. 该 GNN 编码器设计灵活. 我们发现 GAT或 GraphSAGE的性能都很好。在训练过程中，两个图共享每一层的可训练参数矩阵\(W^{(l)}\).

Step-3: Shared MLP

在 GNN 编码器之后, 我们使用一个共享的多层感知器 (MLP) \(g(·)\) 作为投影头, 以增强输出表示的表达能力

Step-4: Channel-level contrastive objective

共享的 MLP 输出两个表示矩阵 \(H,H_a \in R^{N×d}\) , 对于 \(G\) 其采样的增强视图 \(G_a\), 可以看作是两个图视图上具有 \(d\) 通道的两个信号。与之前的研究侧重于节点级对比的计算成本较高的方法不同，我们提供了一种在通道级生成对比对的替代方法. 具体来说, 如图 \(1\) 所示, . 然后,第 \(i\) 个通道分别表示定义为 \(c_i\) 和 \(c_i^a\), 就是输入嵌入 \(H\) 和 \(H_a\) 的第 \(i\) 列, 然后对比目标是最大化两个表示矩阵之间的一致性, 使相同的通道图间正对 \(c_i, c_i^a\) 的分布被拉到一起, 而不同的通道 \(c_i,c_{j \neq i}^{a}\) 负对被推开. 因此, 对通道的损耗函数 \((c_i, c^a_i)\) 定义为:

\[\ell_i = - (\log \frac{\exp(\phi(c_i,c_i^a)/\tau)}{\sum_{j = 1, j\neq i}^{d} \exp(\phi(c_i,c_j^a)/\tau)} + \log \frac{(\exp(c_i,c_i^a)/\tau)}{\sum_{j = 1, j\neq i}^{d} \exp(\phi(c_j, c_i^a)/\tau)}) \]

其中 \(\tau\) 为表示余弦相似度 \(\phi(\cdot,\cdot) = \frac{.T.}{\|\cdot\|\|\cdot\|}\). 发现一个适当的 \(\tau\) 值可以帮助模型从困难的负数中学习. 考虑所有信道, 总对比损耗函数为:

\[\mathcal{L}_{cont} = \frac{1}{d} \sum_i^d \ell_i \]

预测 GNN 编码器和 MLP 都是在无监督的方式训练. 训练阶段结束后, 原始的 \(G\) 喂入 GNN 编码器, 生成结果节点嵌入 \(Z\), 如图1所示. 然后我们可以将其应用于下游的预测任务, 如节点分类或链接预测.

实验

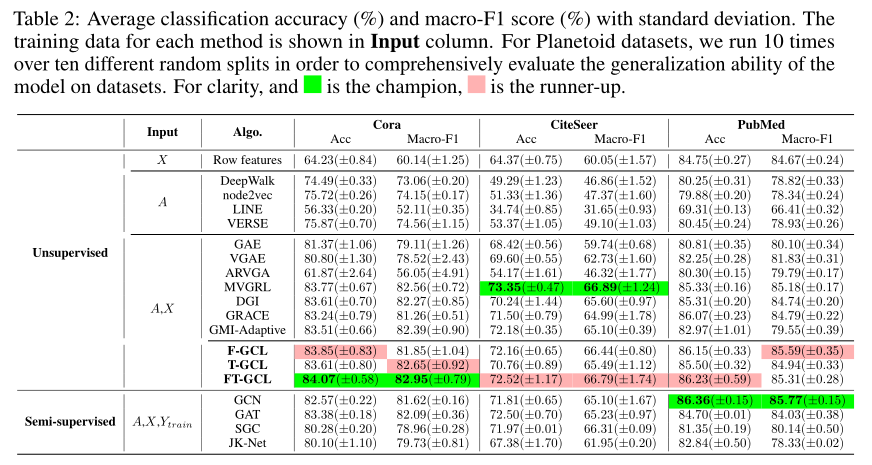
节点分类任务上有较好的表现

结论

提出了一种基于对比学习的自监督表示学习框架 FT-GCL. FT-GCL 旨在根据节点相似度的不同定义, 保留多种类型的邻近信息. 在 FT-GCL 中, 提出了基于特征相似度和局部拓扑相似度的基于接近度的图视图, 然后使用一个对比目标来最大化视图与原始图的一致性. 特别是, 在信道水平上构建了对比对, 这样可以大大减少负对的数量. 我们展示了 InfoNCE 和 FT-GCL 目标之间的联系. 这证明了模型的合理性