GRAPH-BERT: Only Attention is Needed for Learning Graph Representations

动机

• 在当前的主流的图神经网络中过度依赖边的连接, 导致产生了假死问题, 过平滑问题和图的内在互联行阻止了图的并行化.

贡献

• 提出了一种新的图训练模型 Graph-BERT, 该模型表示学习不依赖于图的连接所以有效的解决假死问题, 当然该模型训练会采样无连接子图(目标节点以及它的上下文), 比现有的输入完整图结构的 gnn 更有效. 更准确地说, Graph-BERT 的训练成本仅由训练实例数和采样子图的大小决定, 而子图的大小与输入图的大小完全不相关.
• 无监督预训练, 给定输入的无标签图, 将基于图研究中两个常见的任务节点属性重构和图结构重构, 对 Graph-BERT 进行预训练. 节点属性重构保证了学习后的节点表示能够捕获输入的属性信息; 而图结构重构可以进一步保证 GRAPH-BERT使用无链接子图的学习仍然能够保持图的局部和全局结构属性
• 微调和迁移, 根据特定的应用程序任务目标, Graph-BERT 模型可以进一步微调, 以使学习到的表示适应特定的应用程序需求, 例如节点分类和图集群. 同时, 预训练的 Graph-BERT 也可以被转移和应用到其他序列模型中, 从而可以构建用于图学习的功能管道

思想

符号表示

小写字母 \(x\) 表示标量, 粗体小写字母 \(\pmb{x}\) 表示列向量, 大写字母 \(X\) 表示矩阵, 斜体大写 \(\mathcal{X}\) 表示集合或高阶张量, \(X(i,:)\) 或者 \(X(;,j)\) 表示 \(i_{th}\) 行或者 \(j_{th}\) 列, \((i_{th}, j_{th})\) 表示为 \(X(i,j)\)

框架

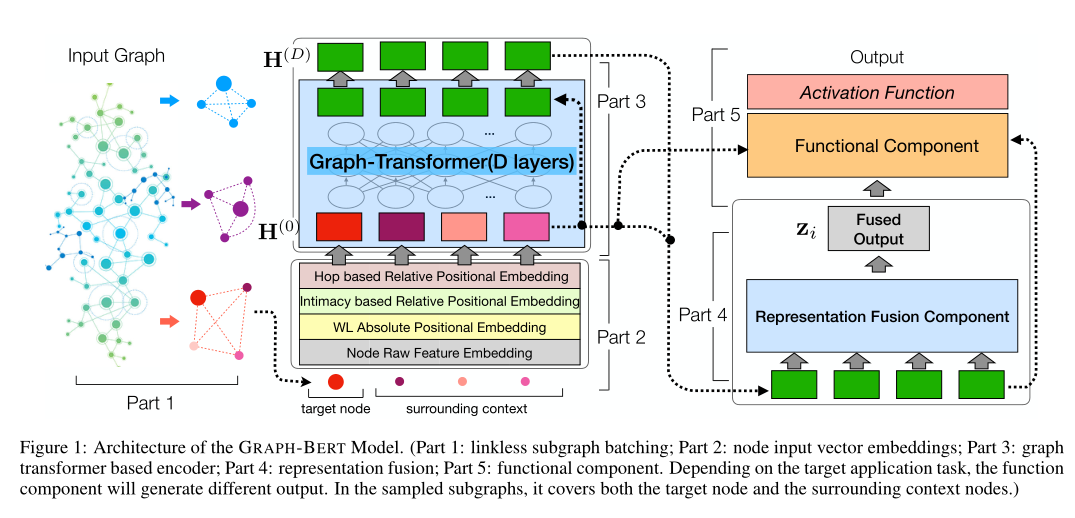
首先采样生成一个无边子图, 然后利用原始的特征进行四个计算, 然后聚合进行 Transformer 后得到最终的全连接表示

架构

Linkless Subgraph Batching

对输入的完整图进行采样, 然而, 为了控制采样过程中的随机性, 本文引入了 top-k亲密采样方法. 这样的抽样算法是基于图亲密矩阵 \(S \in \mathbb{R}^{\mathcal{|V|}\times \mathcal{|V|}}\), 其中 \(S(i,j)\) 度量了节点 \(v_i, v_j\) 之间的亲密度得分, 其中 \(S\) 计算如下:

\[S = \alpha \cdot (I - (1 - \alpha) \cdot \bar{A})^{-1} ~~~~~~~~~~~~(1) \]

其中 \(\alpha\) 为超参数, 一般设置为 \(0.15\), 形式上，对于任意目标 \(v_i \in \mathcal{V}\) 的输入图, 基于亲密矩阵 \(S\), 我们可以定义其学习上下文如下:

\[\Gamma{(v_i)} = \{v_j | v_j \in \mathcal{V} ~~\setminus~~{v_i} \land S(i,j) > \theta_i \} \]

其中 \(\theta_{i}\) 为最小亲密度分数阈值.

Node Input Vector Embeddings

采样后的图的节点是无序的, 可以根据其亲密度进行排序. 一个节点的 embeding 由四部分组成

Raw Feature V ector Embedding

形式上，对于子图 \(g_i\) 中的每个节点 \(v_j \in \mathcal{V}_i\), 可以将其原始特征向量与其原始特征向量向量 \(x_j\) 嵌入到共享的特征空间(同维\(d_h\))中, 可以表示为:

\[e_j^{(x)} = Embed(x_j) \in \mathbb{R}^{d_h \times 1} ~~~~~~~~~~~~~~~(2) \]

根据输入的原始特征属性, 可以使用不同的模型来定义嵌入函数$ (\cdot)$. 例如, CNN 可以使用 \(x_j\) 表示图像; LSTM/BERT 可用于表示文本; 简单的全连接层也可以用于简单的属性输入

Weisfeiler-Lehman Absolute Role Embedding

Weisfeiler-Lehman算法是用来确定两个图是否是同构的, 其基本思路是通过迭代式地聚合邻居节点的信息来判断当前中心节点的独立性(Identity)，从而更新整张图的编码表示:

\[e_{j}^{(r)} = Position-Embed(WL(v_j)) \\ = [\sin(\frac{WL(V_j)}{10000^{frac{2l}{d_h}}}), \cos(\frac{WL(v_j)}{10000 ^\frac{2l + 1}{d_h}})]_{l = 0}^{\frac{d_h}{2}} \]

Intimacy based Relative Positional Embedding

我们将引入一种相对位置嵌入，根据开始时介绍的序列化节点列表的放置顺序提取子图中的局部信息. 形式上, 基于这个序列化的节点列表, 我们可以表示 \(v_j \in \mathcal{V}_i\) 的位置 \(P(v_j)\). 我们知道默认情况下\(P(v_i)=0\), 离 \(v_i\) 更近的节点会有一个较小的位置索引. 此外, \(P(\cdot)\) 是一个变异的位置指标度量. 对于相同的节点 \(v_j\), 它的位置索引 \(P(v_j)\) 对于不同的采样子图是不同的. 在形式上, 对于节点 \(v_j\), 也可以使用上文定义的 Position-Embed(⋅) 函数提取其基于亲和度的相对位置嵌入:

\[e_{j}^{(p)} = Position-Embed(P(v_j)) \in \mathbb{R}^{d_h \times 1} \]

Hop based Relative Distance Embedding

基于跳跃的相对距离嵌入可以作为绝对角色嵌入(对于全局信息)和亲密度相对位置嵌入(对于局部信息)之间的一种平衡. 形式上, 对于子图 \(g_i\) 中的节点 \(v_i \in \mathcal{V}_i\), 我们可以表示它在原始输入图 \(H(v_j;v_i)\)中以跳数为单位的相对距离到达 \(v_j\)，可用来定义它的嵌入向量为:

\[e_j^{(d)} = Position-Embed(H(v_j;v_i)) \in \mathbb{R}^{d_h\times 1} \]

Graph Transformer based Encoder

基于上面定义的计算嵌入向量, 将能够将它们聚合在一起, 以定义子图中节点的初始输入向量, 例如 \(v_j\), 如下所示:

\[h_j^{(0)} = Aggregate(e_{j}^{(x)},e_{j}^{(r)},e_{j}^{(p)},e_{j}^{(d)}) \]

对于子图所有的节点组成的矩阵 \(H^{(0)} = [h_{i}^{(0)},h_{i, 1}^{(0)},...,h_{i,k}^{(0)}]^T \in \mathbb{R}^{(k + 1) \times d_h}\), 下面介绍的基于图形转换器的编码器将使用多层（\(D\) 层) 迭代更新节点的表示，该层的输出可以表示为:

\[H^{(l)} = G-Transformer((H^{(l - 1)})) \\ = softmax(\frac{QK^T}{\sqrt{}d_h}) V + G-Res(H^{(l - 1)}, X_i) \]

其中

\[\begin{cases} Q = H^{(l - 1)}W_{Q}^{(l)}\\ K = H^{(l - 1)}W_{K}^{(l)}\\ V = H^{(l - 1)}W_{V}^{(l)} \end{cases} \]

在上述方程中, \(W_{Q}^{(l)},W_{K}^{(l)},W_{K}^{(l)} \in \mathbb{R}^{d_h \times d_h}\) 表示所涉及的变量. 为了简化论文中的陈述, 假设不同层中节点的隐藏向量具有相同的长度. 符号 \(G-Res(H^{(l-1)}，X_i)\) 表示在中引入的图剩余项, \(X_i \in \mathbb{R}^{(k + 1) \times d_x}\) 表示子图中所有节点的原始特征. 与传统的残差学习不同, 本文将把为目标节点计算的残差项添加到每层子图中所有节点的隐藏状态向量中. 基于上面定义的图形转换器函数, 可以将图形转换器的表示学习过程表示如下:

\[\begin{cases} H^{(0)} = [h_i^{(0)},h_{i,1}^{(0)},...,h_{i,k}^{(0)}]^T, \\ H^{(l)} = G-Transformer(H^{(l - 1)}) ,~~~\forall l \in \{1,2,..,D\} \\ z_i = Fusion(H^{(D)}) \\ \end{cases} \]

GRAPH-BERTLearning

预训练

对于预训练来说它的前置任务主要是节点属性重构和图结构重构

属性重构:

\[\ell_1 = \frac{1}{|\mathcal{V}|} \sum_{v_i \in \mathcal{V}} \|x_i - \hat{x}_i \|_2 \]

图结构重构:

\[\ell_2 = \frac{1}{|\mathcal{V}^2|}\|S - \hat{S}\|_F^{2}\\ \hat{S} \in \mathbb{R}^{|\mathcal{V} |\times |\mathcal{V}|} ~~~~~~~~~~~~~~~~~~~ \hat{S}(i, j) = \hat{s}_{i,j} ~~~~~~~~~~~ \hat{s}_{i,j} = \frac{z_i^Tz_j}{\|z_i\|\|z_j\|} \]

模型迁移和微调

节点分类:

\[\ell_{nc} = \sum_{v_i \in \tau} \sum_{m = 1}^{d_y} -y_i(m) \log \hat{y}_i(m) \]

图聚类:

\[min_{\mu_1,...\mu_{\ell}} min_{\mathcal{C}} \sum _{j = 1}^{l} \sum_{v_i \in \mathcal{C}_j} \|z_i - \mu_j\|_2 \]

实验

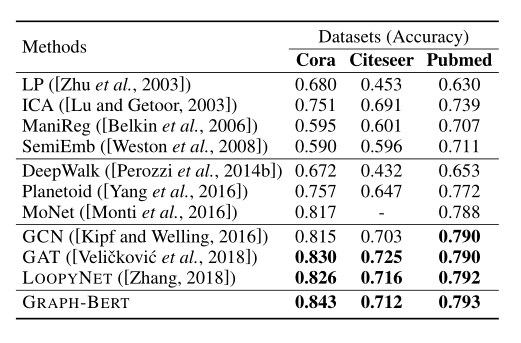
总结

引入了新的用于图表示学习的GRAPH-BERT模型. 与现有的 gnn 不同, GRAPH-Bert 在深度架构中工作良好, 不会遭受其他 gnn 的常见问题 . 基于从原始图数据中采样的一批无链接子图, GRAPH-Bert 可以有效地学习目标节点的表示, 本文引入了扩展的 graph-transformer 层. GRAPH-BERT 作为图学习流水线中的图表示学习组件. 预先训练好的 GRAPH-Bert 可以直接或通过必要的微调转移并应用于解决新的任务.