半监督- Distance-wise Graph Contrastive Learning

标签: 对比学习、图神经网络、半监督

动机

• 在现有的对比学习方法中都存在一个共同的问题, 忽略了任务信息在图节点间不均匀分布, 当 GNN 在学习中, 任务信息的传播在有标签的节点通过边传到无标签的节点, 导致了任务信息在图中没有均匀的分布, 使得模型学习节点嵌入的时候随着到标签节点距离的增加而衰减. 实质上就是距离有标签节点较远的节点没有得到充分的信息.

​

贡献

• 为了使与标签节点较远的节点上能够更加充分得到信息, 提出了一种基于距离的图破坏机制和丢失调度.
• 考虑其 Group PageRank 分布的 KL 散度来度量节点之间的相对距离

思想

符号

节点特征 \(X \in \mathbb{R}^{n \times f}\) , 邻接矩阵 \(A \in \mathbb{R}^{n\times n}\), 有标签的节点为 \(L\), 没有标签的节点 \(U\), 半监督任务训练分类器 \(\mathcal{F}\) , 预测节点的标签 \(y\) .

技术

Group PageRank

Group PageRank 度量标签节点的监督信息. 基于图的 SSL 将节点和邻接特征作为输入, 用来度量从标记节点接受到的信息. 关注邻接特征, 屏蔽节点特征. 以区分图拓扑和节点嵌入的影响, 实质上, 就是对 PageRank 算法进行了分组和向量化的修改, 将其扩展到基于图形的 SSL 中.

原始的 PageRank 算法形式如下:

\[\pi_{pr} = (1 - \alpha)A'\pi_{pr} - \alpha I ~~~~~~~~~~~~~~~~(1) \]

其中 \(A' = AD^{-1}\), \(D\) 是度矩阵, \(I \in \mathbb{R}^n\) 是一个转移向量其中每个值都为 \(\frac{1}{n}\), \(\alpha \in (0, 1])\) 表示随机游走的重置的概率. 而在本算法中. 我们希望测量一组节点对影响. 使随机游走在概率为 \(\alpha\) 的组中的一个随机节点上重新开始, 这就是 Group PageRank:

\[\pi_{Gpr} = (1 - \alpha)A'\pi_{Gpr} - \alpha I_c ~~~~~~~~~~~~~~~~~~~(2) \]

其中 \(c \in [0, k)\) 是 \(k\) 中类别中的一个下表, \(I_c \in \mathbb{R}^n\) 是一个转移向量.

\[I_c^i \begin{cases} \frac{1}{|L_c|}, ~~~ i-th~node~is~a~labeled~node~of~classc \\ 0, ~~~~otherwise \end{cases}~~~~~~~~~~~~~~~~~~~~~~(3) \]

\(L_c\) 定义为有标签节点集合 \(c\), 我们为每组集合单独计算 Group PageRank 然后连接所有的 Group PageRank 向量得到最终的 Group PageRank 矩阵 \(Z \in \mathbb{R}^{n \times k}\) , \(Z_{i,j}\) 表示类 \(i\) 在节点上 \(j\) 上的影响, 实际上可以并行计算 Group PageRank 矩阵 \(Z\):

\[Z = \alpha(E - (1 - \alpha)A')^{-1}I^{*} ~~~~~~~~~~~~~~~~~~~~~(4) \]

\(E\) 是单位矩阵, \(I^{*} \in \mathbb{R}^{n*k}\) 是 \(I_c\) 的串联.

Topology Information Gain(TIG)

采用约定拓扑信息增益 (TIG) 描述节点沿图拓扑从信息源 (标签节点) 获得的任务信息有效性. 理想情况下, 每个节点接收到的信息应该是集中在一个类别上, 这意味着监督信息是强大而清晰, 因此, 我们将向量 \(z_i\) 中最大项作为节点 \(i\) 中最有效的信息类型, 而其他项是混淆信息, 第 \(i\) 个节点 \(T_i\) 的 TIG 值计算如下:

\[Z_{i,c}^{*} = \frac{1}{2}Z_{i,c}(1 + \frac{X_i\mathcal{P}_{c}^{T}}{\|X_i\|\|\mathcal{P}_c\|}) ~~~~~~~~~~ \mathcal{P}_c = \frac{1}{|L_c|} \sum_{i \in L_c} X_i ~~~~~~~(5)\\ T_i = max(Z_{i}^{*}) - \lambda \frac{(\sum_{c = 0}^{k - 1}Z_{i,c}^{*}) - max(Z_i^{*})}{k - 1} ~~~~~~~~~~~~~~~~~~~~(6) \]

\(max(\cdot)\) 是一个最大值函数, \(\lambda\) 是混淆其他类型信息的惩罚因子. \(\mathcal{P_c}\) 是通过平均类 \(c\) 中所有注释节点的嵌入来表示类的原型嵌入,我们假设每个未标记节点对来自不同类别的信息都有自己的特殊偏好，并从节点特征视图中采用嵌入节点 \(X_i\) 和 \(\mathcal{P_c}\) 之间的余弦相似度来调整原始的 Group PageRank值 \(Z_i\)

算法

Distance-wise Graph Perturbation

有限的图扰动更有可能发生在图学习监督信息不足的局部子图上, 因此, 本文的方法是根据 TIG 值对样本节点进行摇动, 当一个节点的 TIG 值较低时, 该节点被选择进行增广的概率较高. 另外, 考虑到节点扩展的扩张性, 通过降低扩展节点周围子图的概率来动态调整选择概率.

Distance-wise Contrastive Pair Sampling

我们对节点相对距离的测量主要取决于节点的 Group PageRank 的差异, 包含全局拓扑信息和标签信息。具体来说，我们对 Group PageRank 向量进行归一化, 然后计算节点之间的 Kullback-Leibler 散度\((KL(·，·))\) 作为全局拓扑距离:

\[D_{i,j}^{g} = KL(p_i, p_j) ~~~~ with ~~~~~ p_i = NORM(Z_{i}^{*}) ~~~~~~~~~~~~(7) \]

\(NORM(\cdot)\) 是将原始的 Group PageRank 向量 \(Z_i^{*}\) 转化为所有类别的概率分布的归一化函数. 此外, 从局部拓扑距离和节点初始嵌入距离的角度补充了相对距离测量, 对于节点局部拓扑距离 \(D_{i,j}^{l}\), 使用最小跳数作为指标. 对于节点的嵌入距离 \(D^{e}_{i,j}\), 计算节点嵌入矩阵之间的余弦距离. 最终节点相对距离由全局/局部拓扑距离与节点嵌入距离的加权和计算:

\[D_{i,j} = S(D_{i,j}^{g}) + \lambda_1S(D_{i,j}^{l}) + \lambda_2S(D_{i,j}^{e}) ~~~~~~~~~~~~~~~~~~(8) \]

\(\lambda_1， \lambda_2\) 为两个补充项的权重, \(S(·)\) 表示将原始值转移到 \([0,1]\) 的尺度运算.

然后我们分别为每个节点构造正对和负对。对于第 \(i\) 个节点(锚节点)，正样本集 \(P_i\) 由最近且相对距离最小的节点组成; 对于负集 \(N_i\), 我们建议采样半困难节点; 既不太远也不太靠近锚节点。考虑到个性化排序的节点由 \(D_i\) 从最小到最大(第 \(i\) 个节点本身被排除)，\(P_i、 N_i\) 分别从 \(R_i\) 中截断:

\[P_{i} = R_{i}[0:post_{end}], N_{i} = R_{i}[negt_{beg}:negt_{end}] ~~~~~~~~~~~~~~(9) \]

The Complete DwGCL Framework

对于一个 GNN 编码器 \(\mathcal{F}\), 有监督的交叉损失函数 \(\mathcal{L}_{CE}\) 在有标签的集合 \(L\) 上计算:

\[t = \mathcal{F}(X,A,\theta) ~~~~~~~~~~~~~~(10)\\ \mathcal{L}_{CE} = -\frac{1}{|L|}\sum_{i \in L} \sum_{c = 0}^{k - 1}y_i \log p(t_{i}^{c}, \tau) ~~~~~~~~~~~~~~~~~(11) \]

\(t_i\) 是 GNN 对于节点 \(i\) 的输出, \(y_i\) 是原始标签, \(\theta\) 是编码器 \(\mathcal{F}\) 的参数; \(p(t_i)\) 是 \(t_i\) 经过带温度的 \(\tau\) 的 softmax 函数的的输出. 除了有监督损失外，DwGCL 还包括三种无监督对比损失:自身前后一致性损失、正对对比损失和负对对比损失. 自身前后一致性损失通过以下公式计算:

\[\mathcal{L}_{s}^{i} = KL(\mathcal{F}(X_p, A_p, \theta)_i, \mathcal{F}(X, A,\widetilde{\theta})_i) ~~~~~~~~~~~~(12) \]

其中增强的节点的特征矩阵 \(X_p\) 和邻接矩阵 \(A_p\) 都是通过 distance-wise 图扰动. \(\widetilde{\theta}\) 是固定的当前参数 \(\theta\) 的副本, 梯度不传播 \(\widetilde{\theta}\) . 同样, 计算正负对的对比损失:

\[\mathcal{L}_{p}^{i} = \frac{1}{|P_i|} \sum_{j \in P_i} KL(\mathcal{F}(X_p, A_p, \theta)_i, \mathcal{F}(X_p, A_p, \widetilde{\theta})_j) ~~~~~~~~(13)\\ \mathcal{L}_{n}^{i} = \frac{1}{|N_i|} \sum_{j \in N_i} KL(\mathcal{F}(X_p, A_p, \theta)_i, \mathcal{F}(X_p, A_p, \widetilde{\theta})_j) ~~~~~~~~(14)\\ \]

\(KL\) 散列作为对比对相似度度量的得分函数, 实证结果表明, 对于低维GNN输出, \(KL\) 散列比内部产生更稳定和有效. 我们推测原因是由于最后一个 GNN 编码层通常同时作为分类器层, 因此低维logits向量之间的内部生成不具有鲁棒性, 给GNN训练带来了混淆信号, 然后按以下方式计算节点 \(i\) 上的完全无监督损失:

\[\mathcal{L}_{U}^{i} = \mathcal{L}_{s}^{i} + \mu_1\mathcal{L}_{p}^{i} + \mu_2\mathcal{L}_{n}^{i} ~~~~~~~~~~~~~~~~(15) \]

\(\mu_1\) 和 \(\mu_2\) 分别是正对和负对的损失重量。实验表明，当 \(\mu_1\) 为 \(\mu_2\) 的 \(2-3\) 倍时, 模型最优. 代替现有的所有 GCL在整个图上均匀地加入CL损失和监督损失, 提出根据不同子图接收监督信息的量自适应地调整 CL 损失权重. 具体来说, 使用基于节点 TIG 值的余弦退火调度来不同地设置每个节点的 CL权重:

\[w_i=w_{min}+ \frac{1}{2} (w_{\max}−w_{\min})(1 + \cos(\frac{Rank(T_i)}{n}\pi)) ~~~~~~~~~~~~(16) \]

\(w_{\min}、w_{\max}\) 分别为 CL 损失的最小值和最大值; \(Rank(T_i)\) 为 \(T_i\) 从最小到最大的排序顺序. 然后将有监督损失和无监督损失按距离组合为最终损失:

\[\mathcal{L}=\mathcal{L}_{CE} + \frac{1}{n}\sum_{i = 1}^{n - 1}w_i\mathcal{L}_{U}^i~~~~~~~~~~~~~~~(17) \]

这样，从图中接收到较少监督信息的子图可以从CL 的补充信息中获益

伪码

实验

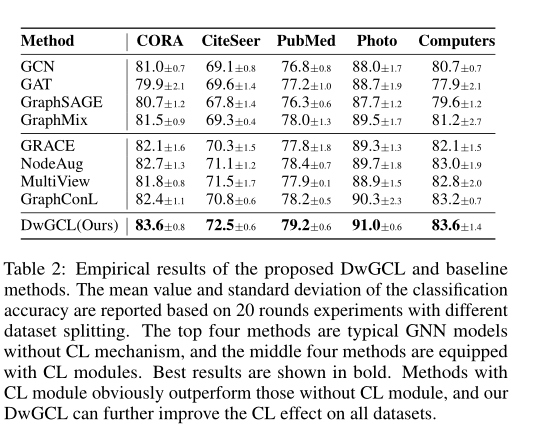
半监督上的节点分类

总结

研究了基于图的半监督学习中的对比学习. 指出当前的图对比学习方法缺乏对任务信息在图上分布不均的考虑. 研究表明, 对比学习在图学习中所带来的好处主要来自于拓扑上远离信息源的节点, 这些节点缺乏来自图的足够任务信息, 而可以通过对比学习获得补充监督. 基于研究结果, 提出了基于距离的图对比学习框架. 以提高 CL 在图学习中的效果. 我们设计了一个基于距离的图扰动策略和一个 CL 减重调度机制, 以加强远离信息源的节点的学习. 还提出了一种新的对比对采样方法, 该方法同时考虑了每个节点的拓扑特征和特征嵌入, 进一步提高了对比对的构造效率. 在五个基准上的综合实验表明，DwGCL 方法比以往的方法更有优势。通过对各种图半监督学习场景的进一步分析，证明了该方法的通用性