图扩散-Diffusion Improves Graph Learning

图扩散-Diffusion Improves Graph Learning

标签：图神经网络、扩散技术

动机

• 图卷积的核心就是图神经网络，就是在一跳邻居节点上进行消息传递，这些消息在每个节点聚合，形成下一层的嵌入。虽然神经网络确实利用了更深层的高阶邻域，但将每一层的消息限制在一跳邻居似乎是随意的武断的。实图中的边通常是有噪声的或使用任意阈值定义的

贡献

• 提出图扩散卷积 (GDC)，这是一种更强大、更通用、更空间局部化的消息传递替代方法，它使用稀疏化的图扩散的广义形式。GDC不限于GNNs，可以与任何基于图的模型或算法相结合
• 分析了 GDC 和图扩散的光谱特性，展示了如何将图扩散技术表示为等价多项式滤波器，并分析了GDC 对图谱的影响

思想

符号说明：

\(S\) 为扩散后得到的图，\(T\) 为转移矩阵，\(\theta\) 为加权系数， 一个无向图 \(G=\{V,\varepsilon\}\) ，其中 \(V\) 为顶点集合，\(\varepsilon\) 为边集，定义 \(N = |V|\) 为点的个数， 邻接矩阵 \(A \in R^{N×N}\) ，\(D\) 为一个度矩阵，对角线上的值为每个点的度数，\(I_N \in N×N\) 为单位矩阵，\(w_{loop} \in R^+\)

核心

\[S = \sum_{k = 1}^{\infty}{\theta}_k T^k ~~~~~~~~~~~~~~~~~~~~~~~~~~~(1) \]

上式为扩散技术的核心

转移矩阵

• \(T\) 在一个无向图进行随机游走 (random walk) 的转移矩阵 (列随机)：

  \[T_{rw}= AD^{-1} \]

• 对称矩阵：

  \[T_{sym} = D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \\ D_{ii} = \sum_{j = 1}^{N}A_{ij} \]

• 还通过向原始邻接矩阵添加(加权)自环来调整随机游走：

  \[\tilde{T_{sym}} = (w_{loop}I_N + D)^{-\frac{1}{2}}(w_{loop}I_N + A)(w_{loop}I_N + D)^{-\frac{1}{2}} \]

特殊的例子

• PPR (personalized PageRank)：

  \[T = T_{rw} ~~~~~~ {\theta_k^{PPR}} = \alpha(1 - \alpha)^k \]

  传输概率 \(\alpha \in (0,1)\)

• 热核 (heat kernel)：

  \[T = T_{rw} ~~~~~~ {\theta_k^{HK}} = r^{-t}\frac{t^k}{k!} \]

框架

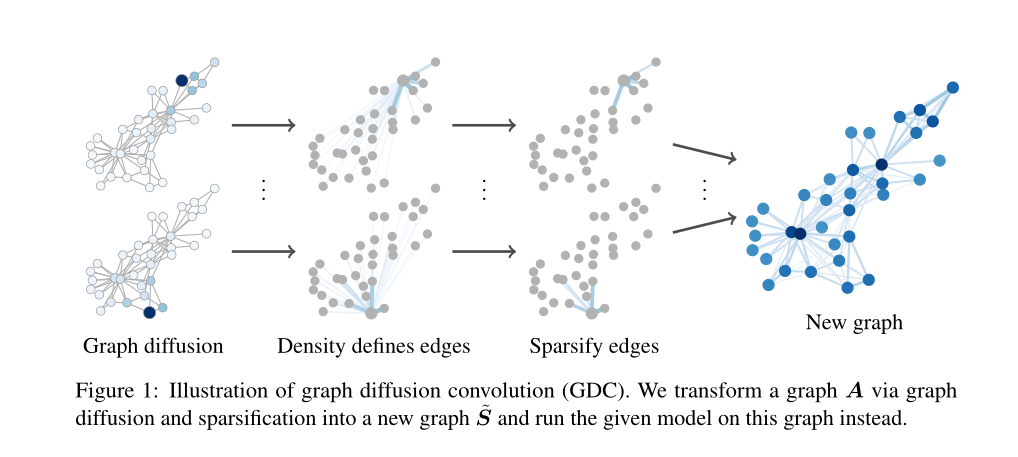
首先是对原图进行使用公式 \((1)\) 进行扩散，扩散后得到一个稠密图，再在两个稀疏化的方法中选择一个进行稀疏化后得到最终的图

实验

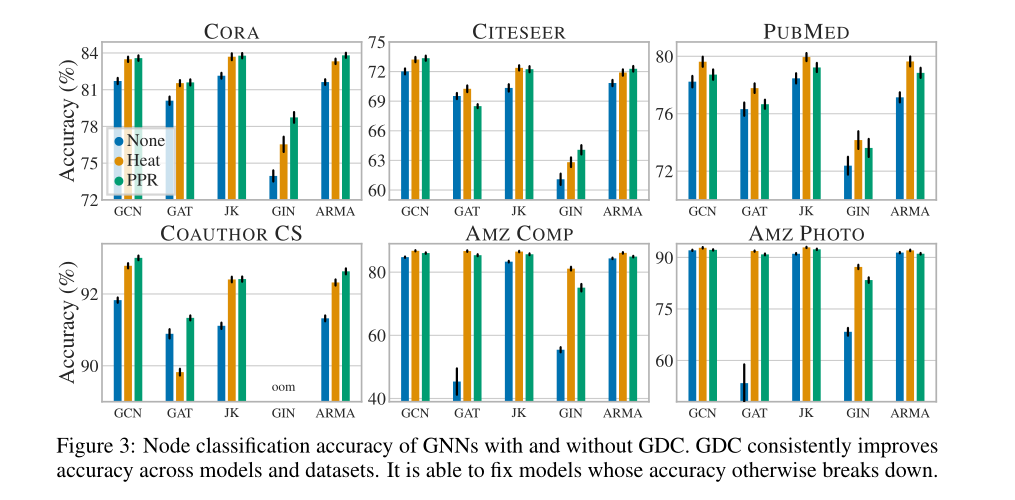
在节点分类上的准确率，是将扩散技术与之相融合