自监督-Iterative Graph Self-distillation

自监督-Iterative Graph Self-distillation

标签：自监督、图神经、知识蒸馏、图学习、对比学习

动机

• 在各个领域图是普遍存在，虽然最近的图神经网络 GNN 在节点表示和图表示方面有很大的进展，其都是通过聚合邻居信息结合自身信息并通过非线性变换，但是这些网络的一个关键是需要大量的带有标签化的数据才有很有的性能展示
• 虽然借鉴了图像领域或者文本领域的自我监督表征学习，但是大多是遵循代理任务（前置任务）的自监督预处理范式或者通过 InfoMax 原理进行对比学习，前者需要精细的设置，而对比学习通过构造正负样本最大化互信息，并且需要额外的判别器对局部-全局对和负样本进行评分

贡献

• 提出了一种图上自蒸馏框架 ---- IGSD，主要用于自监督学习上的图表示学习
• 进一步将IGSD扩展到半监督场景，在该场景中，通过监督对比损失和自我训练有效地利用了标记数据
• IGSD在半监督图分类和分子性质预测任务中超越了最先进的方法，并在自监督图分类任务中实现了与最先进的方法相竞争的性能

思想

核心

在对比学习的框架下，结合自蒸馏技术使得教师网络同时对学生网络进行训练

框架

对于一个图数据集合首先进行分批，对于三个原图 \(G_1、G_2、G_3\)，利用扩散技术对原图进行增强得到 \(G_1'、G_2'、G_3'\)，

都经过一个编码器 Encoder \(f_{\theta}\)：

\[h = f_{\theta}(G)\\ h_v^k = \sigma(W^k·CONCAT(h_v^{k - 1}, AGGREGATE(\{h_u^{k - 1} \quad \forall u \in N(v) \}))) \]

通过编码器得到一个图的表示 \(h\) 后经过一个投影头 \(g_{\theta}\)（两层的MLP）：

\[z = g_{\theta}(h)\\ g_{\theta}(h) = W^{(2)}\sigma(w^{(1)}h) \]

投影后得到 \(z\) ，对于学生网络我们还有一个预测器 \(h_{\theta}\)：

\[h_{\theta} (z) = W^{(2)}\sigma(W^{(1)}z) \]

得到 \(z、h_{\theta}(z)\) ，我们在潜在空间使用 \(L_2\) 范式得到一个近似输入空间中的语义距离，并且一致性损失可以被定义为会议话预测之间的均方误差

\[L^{con}(G_i,G_j) = ||h_{\theta}(z_i) - z_j'||_2^2 + ||h_{\theta}(z_i') - z_j||_2^2 \]

由于一致性损失，教师网络提供了一个回归目标来训练学生网络，并且使用梯度更新了学生网络的权重之后，使用 EMA（exponential moving average 指数移动平均） 更新教师网络的权重：

\[{\theta}_t' \leftarrow \tau{\theta}_{t - 1}' + (1 - \tau){\theta}_t \]

数据增强

• 在数据加强方面通过图扩散和稀疏化将带有转移矩阵 \(T\) 的图 \(G\) 变换为带有邻接矩阵 \(S\) 的新图：

  \[S = \sum_{k = 0} ^ {\infty}{\theta}_kT^k \\ {\theta}_k^{PPR} = {\alpha}(1 - \alpha)^k \\ \]

• 另一中方法是随机移除边达到破坏图的效果

损失函数

在自监督学习中，为了对比 锚点（anchor）\(G_i\) 和其他负样例 \(G_j\) ，采用一下目标函数：

\[L^{self-sup} = -E_{G_i G} [\frac{exp(-L_{i,i}^{con})}{exp(-L_{i,i}^{con}) + \sum_{j = 1}^{N-1}I_{i≠j}exp(-L_{i,j}^{con})}] \]

在最后的图表示中，我们利用混合函数获得最后图的表示：

\[Mix_{\lambda}(a, b) = {\lambda} a + (1 - {\lambda})b \\ \hat{h} = Mix_{\lambda}(h, h')\\ h = f_{\theta}(G) ~~~~~~~~~~~~ h' = f_{\theta'}(G) \]

在半监督学习中，可以使用少量的标记数据来进一步概括相似性损失，以处理任意数量的属于同一类的正样本：

\[L^{supcon} = \sum_{i = 1}^{Kl}\frac{1}{KN_{y'}}\sum_{j=1}^{Kl}I_{i≠j}I_{y_i'≠y_j'}L^{con}(G_i, G_j) \]

最后半监督的损失函数：

\[L^{semi}=L(G_L,{\theta}) + wL^{self-sup}(G_L ∪G_U, \theta) + w'L^{supcon}(G_L,\theta) \]

实验

自监督学习中图分类任务的准确率

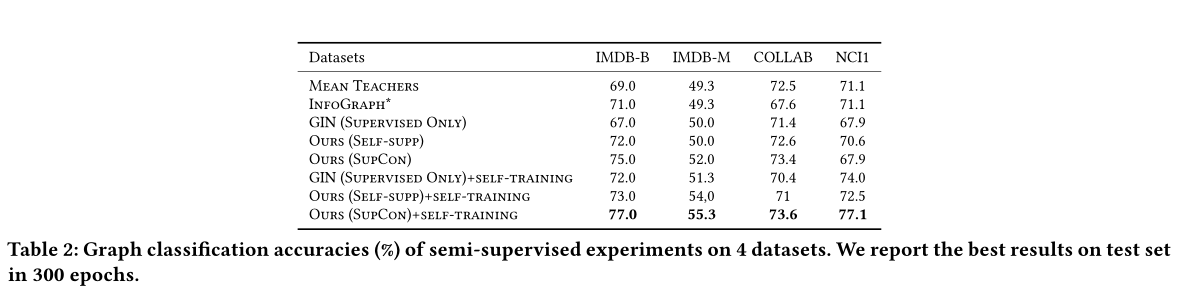
半监督下进行图分类任务的准确率

结论

在本文中，提出了IGSD，一个新的图级表示学习框架，通过自我蒸馏。我们的框架通过对图实例的增广视图进行实例判别来迭代执行师生蒸馏。