自监督-SelfGNN: Self-supervised Graph Neural Networks without explicit negative sampling

自监督-SelfGNN: Self-supervised Graph Neural Networks without explicit negative sampling

标签：自监督、图神经网络、对比学习

动机

• 在真实世界中许多数据大部分是有没有标签的，而打上标签的是需要很大花费的

• 现存的对比学习框架关键主要是对数据加强并生成正负样本对，而最近在 CV 中提出了隐式对比学习，没有明确需要负样本对，而在 GNN 中目前还没有进行探索

贡献

• 主要提出了隐式的对比学习，没有明确需要负样本对，其主要参考的是 Siamese network 设计方式进行对图神经的设计，大大减少了负样本对的设计
• 介绍了四种特征增强方式和一种拓扑增强方式

思想

核心

两个方面---数据加强（分别在图结构和属性方面做了增强）和网络设计（模仿 Siamese network 设计方式，目的丢弃负样本）

框架

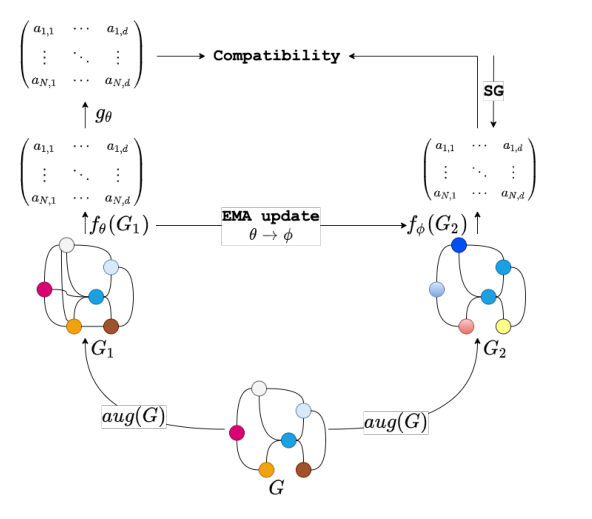
对于一个原图 \(G\)，我们分别进行数据增强得到两个加强图 \(G_1, G_2\)，分别利用两个 GNN encoder （\(f_{\theta}、f_{\phi}\) 其编码器的参数分别是 \(\theta、\phi\)）进行对两个增强图数据进行编码。并在 \(f_{\theta}\) 在应用一个 prediction block \(g_{\theta}\)（MLP ），对于 \({\theta}\) 的更行主要用到对比损失函数，对比的经过 prediction block得到的 \(X_1\) 和 经过编码器 \(f_{\phi}\) 得到的 \(X_2\)。而对于 \(\phi\) 主要是通过 \(\theta\) 进行 EMA（指数移动平均）进行更新。（假设左边部分为 student network，用 s-n 表示，右边部分为 teacher network，用 t-n 表示）

数据增强

Topology augmentation

​ 拓扑数据扩充的目的是通过利用图结构的属性来揭示原始图的不同拓扑视图，在本文中，主要引用了两种 pageRank 算法，一种是 pageRank 基于随机游走的 pageRank-PPR 和 热核 (head-kernel) pageRank-HK， 并且提出了第三种基于卡兹索引的高阶网络构建技术

​ pageRank-PPR：\(H^{PPR} = \alpha(I - (1 - \alpha) \widetilde{A})^{-1}\)

​ pageRank-HK：\(H^{HK} = exp(tAD^{-1}-t)\)

​ pageRank-KATZ：\(H^{katz} = (I-\beta\widetilde{A})\beta \widetilde{A}\)

feature augmentation

• split (切分)：将特征进行切分，在数据增强成为两个视图时，将特征分成两部分分别分到两个视图中
• Stadardize (标准化)：将特征进行放缩，\(X' = (\frac{X^T-\bar{x}}{s})\)， \(\bar{x}\) 和 \(s\) 分别时特征的平均值和方差
• Local degree Profile (图度分布)：在一些没有特征的图中我们根据度分布构造 \(5\) 个统计量为节点的特征
• paste (扩充)：利用度分布的 \(5\) 个统计量对原本节点的属性进行扩充

encoder and prediction

encoder

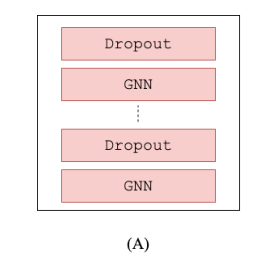
上图为一个 encoder \(f\) , 其主要目的是为了增广后的图进行编码，用于下游任务（并行 GNN）

prediction

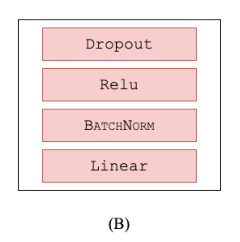
prediction 或者是一个 projection head，其主要对 encoder 后的进行一个映射

在这个架构中主要有两个不同点，一个是 s-n 中有投影头，而 t-n 中没有投影头，对于 s-n 来说，投影头相当于大脑，去学习 t-n 中对图的表示 \(g(X_1) ≈ X_2\)，另一个就是对于编码器参数的更新，s-n 中的参数 \(\theta\) 使用最小化 Loss function 进行 BP 更新参数 \(\theta\) ，而 t-n 中对于并没有利用 BP 更新参数 \(\phi\) ，而是用 s_n 的参数 \(\theta\) 做一个 EMA 去更新 t-n中的参数 \(\phi\)

Loss function and EMA update

Loss function

\[L_{\theta} = 2 - 2 · \frac{<g_{\theta}(X_1),X_2>}{||g_{\theta}(X_1) ||_F ·||(X_2)||_F} \]

EMA update

\[\phi = \tau\phi + (1 - \tau)\theta \]

实验

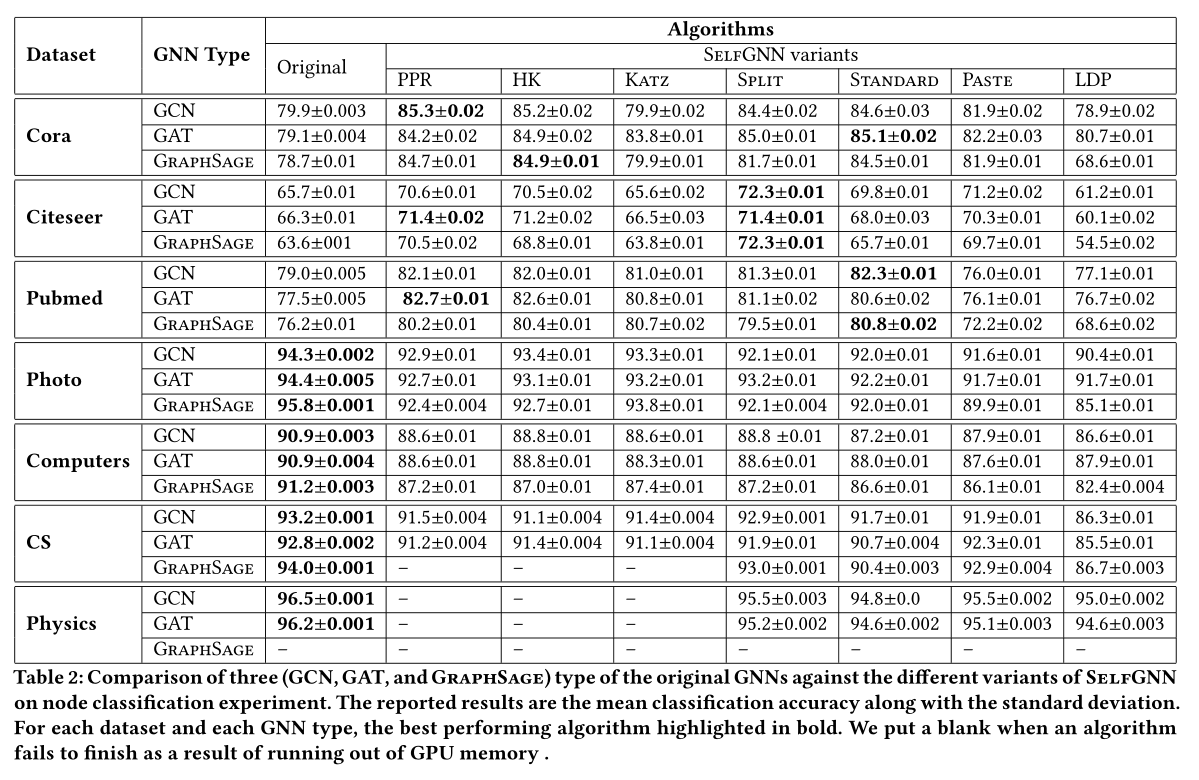
在 7 个数据集中进行节点分类任务，对比结果如上图。前三个引文数据网络数据之所以比较好是因为标签部分少，相对于原始模型。本文提出的自监督方法 Self-GNN 更好，而后面四个数据集不好的原因是对于训练集部分都有标签，相当于完全监督学习，所以对于本文方法没有原始模型的好。