主成分析法-PCA

PCA

解决过拟合的三个方法：

• 提升数据量
• 正则化
• 降维
  • 直接降维（直接选择某些重要的特征）
  • 线性降维（PCA, MDS）
  • 非线性降维（流形，Isomap，LLE）

数据维度过多会导致数据稀疏性增大，形成维度灾难

思想

数据从原来的坐标系转换到新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选择的是原始数据中方差最大的方向，第二个新坐标轴选择和第一个坐标轴正交且具有最大方差的方向。该过程一直重复，重复次数为原始数据中特征的数目。我们会发现，大部分方差都包含在最前面的几个新坐标轴中。因此，我们可以忽略余下的坐标轴，即对数据进行降维处理。

• 一个中心：原始特征空间的重构

​ 找到一组正交基，将一组线性相关特征变换到线性无关

• 两个基本点

  • 最大投影方差

    ​ 使得往某个方向投影后的点尽可能分散，也就是让投影后的点的方差尽可能的大。

    \[假设数据集：data = \{x_1, x_2, ... , x_n\}, x_i \in R^p\\ 数据的中心：\bar{x}_{p×1} = \frac{1}{N}\sum_{i = 1}^N x_i = \frac{1}{N}X^T1_N \\ 1_N = (1, 1, ... , 1)^T_{N×1}\\ 数据的方差：S_{p×p} = \frac{1}{N} \sum_{i = 1}^{N}(x_i - \bar{x})(x_i - \bar{x})^T = \frac{1}{N}X^THX\\ H = I_N-\frac{1}{N}1_N1_N^T \]

    那么投影后的点：

    

    \[s_{projection} = \cos \theta*x_i\\ \because u_1 * x_i = |u_1||x_i|\cos \theta \\ 设\quad |u_1| = 1\\ \therefore u_1 * x_i = |x_i|\cos \theta \\ \therefore s_{projection}= u_1 * x_i \\ \]

    由于要求的是最大投影方差

    \[中心化后的数据： x_i - \bar{x} \\ 投影后的点：(x_i - \bar{x})u_1 \\ 投影方差：((x_i - \bar{x})u_1)*((x_i - \bar{x})u_1)^T =((x_i - \bar{x})u_1)^2 \\ 设： J(u_1) = \frac{1}{N}\sum_{i = 1}^{N}((x_i - \bar{x})u_1)*((x_i - \bar{x})u_1)^T\quad s.t. u_1^Tu_1 = 1 \\ J(u_1) = \frac{1}{N}u_1^T(\sum_{i = 1}^{N}(x_i - \bar{x})(x_i - \bar{x})^T)u_1\\ J(u_1) = u_1^T(\frac{1}{N}\sum_{i = 1}^{N}(x_i - \bar{x})(x_i - \bar{x})^T)u_1 \\ J(u_1) = u_1^TS u_1 \]

    那么该问题变成了带有约束的优化问题：

    \[\begin{cases} \hat{u_1} = argmax_{u_1}(u_1^TS u_1)\\ s.t. \quad u_1^Tu_1 = 1 \end{cases} \]

    用拉格朗日乘子法进行求解：

    \[L(u_1,\lambda) = {u_1}(u_1^TS u_1) + \lambda(1 - u_1^Tu_1) \\ 对该函数进行求导：\\ \frac{\partial L}{\partial u_1} = 2Su_1 - 2 \lambda u_1 \\ 令该函数等于 0 \\ 2Su_1 = 2 \lambda u_1 \\ Su_1 = \lambda u_1 \]

    此时，\(S\) 就为方差矩阵，\(u_1\) 为特征值， \(\lambda\) 为特征向量

    \[\hat{u_1} = argmax_{u_1} u_1^TSu_1 = argmax_{u_1} u_1^T\lambda u_1 argmax_{u_1} \lambda u_1^T u_1 = argmax_{u_1} \lambda \]

    找出投影方差最大的 \(q\) 个维度。

    实际上 PCA 就是找出特征向量中最大的 \(q\) 个维度进行降维

  • 最小重构代价

    ​ 使新的坐标与原坐标之间的差值尽可能小。

    \[中心化：\widetilde{x} = x_i - \bar{x} \\ 令 ||u_i|| = 1 \quad i = 1,2,...,p \\ 重构向量 x_i' = (\widetilde{x}^Tu_1)u_1 + (\widetilde{x}^Tu_2)u_2 \\ 标量：(\widetilde{x}^Tu_1) \quad 方向向量： u_1 \\ \widetilde{x} \in R^p \quad x_i' = \sum_{k = 1}^P(\widetilde{x}u_k)u_k \\ 降维后(丢掉一些信息)：\hat x_i \in R^q(q < p) \quad \hat{x} = \sum_{k = 1}^q(\widetilde{x}u_k)u_k \\ 重构距离： \\ J = \frac{1}{N} \sum_{i = 1}^{N} ||x_i' - \hat{x}||^2\\ =\frac{1}{N} \sum_{i = 1}^{N} \sum_{i = q + 1}^P (\widetilde{x}^Tu_k) ^2\\ = \frac{1}{N} \sum_{i = 1}^{N} \sum_{i = q + 1}^P ((x_i - \bar{x})^Tu_k )^2 \\ \because \sum_{i = 1} ^ N \frac{1}{N} (({x_i - \bar{x}})u_k)^2 = u_k^TSu_k\\ \sum_{k = q + 1}^pu_k^TSu_k (s.t. \quad u_k^Tu_k = 1) \]

    此时又变成了一个带有约束的问题:

    \[\begin{cases} u_k = argmin_{u_k}\sum_{k = q + 1}^pu_k^T Su_k \\ s.t. \quad u_k^Tu_k = 1 \end{cases} \]

    利用拉格朗日乘子法同样可得：

    \[Su_k = \lambda u_k \\ u_k = argmin_{u_k}\sum_{k= q + 1}^{p} u_k^TSu_k = argmin_{u_k}\sum_{k= q + 1}^{p} \lambda_k \]

    找出重构距离影响最小的(p-q) 个维度舍弃。

PCA 算法流程

• 对数据进行去中心化（归一化处理）
• 计算归一化后的数据集的协方差矩阵
• 计算协方差矩阵的特征值和特征向量
• 根据特征值保留最重要的 \(k\) 个特征向量
• 将 \(m*n\) 的数据集乘以 \(k\) 个 \(n\) 维的特征向量 \((n*k)\)，得到最后的降维数据 \(m * k\)

CODE

import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

def pca(data, n_dim):
    # |data| = m * n
    
    # 归一化(中心化、去平均值)  data - mean(data)
    data = data - np.mean(data, axis = 0, keepdims = True)
    
    """
    去中心化后，那么每个维度均值就是为0，投影  方差就是 data^2
    这里数据维度为 4
    那么协方差 cov(x,y,q,p) = [
                                [cov(x, x), cov(x, y), cov(x, q), cov(x, p)]
                                [cov(y, x), cov(y, y), cov(y, q), cov(y, p)]
                                [cov(q, x), cov(q, y), cov(q, q), cov(q, p)]
                                [cov(p, x), cov(p, y), cov(p, q), cov(p, p)]
                            ]
    """
    cov = np.dot(data.T, data)

    # 求方阵解特征值 1 * n 和特征向量 n * n
    eig_values, eig_vector = np.linalg.eig(cov)
    
    # 按照特征值的大小进行排序，此处按照从小到大的值进行排序，并且返回前 n_dim 个数据的下标 |index| = n_dim
    indexs_ = np.argsort(-eig_values)[:n_dim]

    # 提取 index_ 列中的特征向量 n * |index| = n  * n_dim

    picked_eig_vector = eig_vector[:, indexs_]

    # data_dim = m * n  x  n * n_dim = m * n_dim,就是数据降维
    data_ndim = np.dot(data, picked_eig_vector)

    return data_ndim

def highdim_pca(data, n_dim):
    '''

    when n_features(D) >> n_samples(N), highdim_pca is O(N^3)

    :param data: (n_samples, n_features)
    :param n_dim: target dimensions
    :return: (n_samples, n_dim)
    '''
    N = data.shape[0]
    data = data - np.mean(data, axis = 0, keepdims = True)

    Ncov = np.dot(data, data.T)

    Neig_values, Neig_vector = np.linalg.eig(Ncov)
    indexs_ = np.argsort(-Neig_values)[:n_dim]
    Npicked_eig_values = Neig_values[indexs_]
    # print(Npicked_eig_values)
    Npicked_eig_vector = Neig_vector[:, indexs_]
    # print(Npicked_eig_vector.shape)

    picked_eig_vector = np.dot(data.T, Npicked_eig_vector)
    picked_eig_vector = picked_eig_vector/(N*Npicked_eig_values.reshape(-1, n_dim))**0.5
    # print(picked_eig_vector.shape)

    data_ndim = np.dot(data, picked_eig_vector)
    return data_ndim

if __name__ == "__main__":
    data = load_iris()
    X = data.data
    y = data.target
    data_2d1 = pca(X, 2)
    plt.figure(figsize=(8,4))
    plt.subplot(121)
    plt.title("my_PCA")
    plt.scatter(data_2d1[:, 0], data_2d1[:, 1], c = y)

    data_2d2 = data_2d1 = highdim_pca(X, 2)
    plt.subplot(122)
    plt.title("highdim_pca")
    plt.scatter(data_2d2[:, 0], data_2d2[:, 1], c = y)
    plt.show()

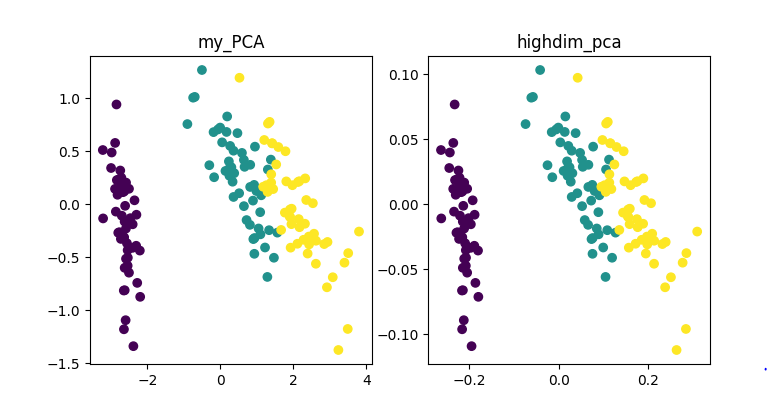
结果