SVM-支持向量机
SVM
svm 解决的是分类问题,目的是在一个数据集中,找到一个超平面,能将数据集正确的分类
svm 三个重要的东西:间隔、对偶、核函数
最大间隔分类器
假设数据集(data):\(\{x_i, y_i\}_{i = 1}^{N}\quad x_i\in R^p、y_i \in \{+1, -1\}\)
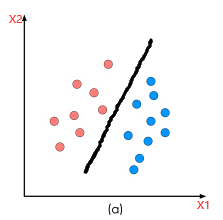
并且我们设超平面为 \(y = \omega x + b\) (黑色部分为超平面)
最大间隔分类器的目的是找到一个超平面,使得这个超平面能正确分类的同时并且到样本点的最小距离最大
\[\begin{cases}
max \quad margin(w, b)\\
s.t
x_i \omega + b > 0 \quad y_i = +1 \\
x_i \omega + b < 0 \quad y_i = -1
\end{cases}
\]
我们对约束条件进行整理得:
\[\begin{cases}
max \quad margin(w, b)\\
s.t \quad
y_i(x_i \omega + b) > 0
\end{cases}
\]
如何定义间隔 margin, 也就是点到面距离
\[margin = min_{w, b, x_i} \frac{1}{||\omega||}|\omega x_i + b|
\]
根据约束条件都是大于 \(0\),对上式去掉绝对值后整理得:
\[\begin{cases}
max_{w, b,} min_{x_i} \frac{1}{||\omega||}y_i(\omega x_i + b)\\
s.t \quad
y_i(x_i \omega + b) > 0
\end{cases}
\]
将 \(\omega\) 提到前面:
\[\begin{cases}
max_{w, b,} \frac{1}{||\omega||} min_{x_i} y_i(\omega x_i + b)\\
s.t \quad
y_i(x_i \omega + b) > 0
\end{cases}
\]
假设:
\[\exists \gamma > 0 \quad min ( y_i(\omega x_i + b)) = \gamma
\]
令 \(\gamma = 1\):
\[\begin{cases}
max_{w, b,} \frac{1}{||\omega||} \\
s.t \quad min( y_i(\omega x_i + b)) = 1 \\
\end{cases}
\]
将 \(min\) 去掉后进行变换得:
\[\begin{cases}
min_{w, b,} \frac{1}{2}{\omega}^T\omega \\
s.t \quad y_i(\omega x_i + b) ≥ 1 \\
\end{cases}
\]
最大间隔分类器变成凸二次规划问题。
将 \(-1\) 进行移项后得:
\[\begin{cases}
min_{w, b,} \frac{1}{2}{\omega}^T\omega \\
s.t \quad 1 - y_i(\omega x_i + b) ≤ 0 \\
\end{cases}
\]
引入拉格朗日乘子:
\[L(\omega, b, \lambda) = \frac{1}{2}{\omega}^T\omega + \sum_{i = 1}^n {\lambda_i(1 - y_i(\omega^Tx_i + b))}
\]
则将带有约束的不等式转化为无约束不等式:
\[\begin{cases}
min_{w, b}max_{\lambda} L(\omega, b, \lambda)\\
s.t.\quad \lambda_i≥0
\end{cases}
\]
由对偶关系:
\[\begin{cases}
max_{\lambda}min_{w, b} L(\omega, b, \lambda)\\
s.t.\quad \lambda_i≥0
\end{cases}
\]
我们求 \(min_{w,b}L(\omega,b,\lambda)\) 时候首先对 \(b\) 求偏导:
\[\frac{\partial L}{\partial b} = \frac{\partial}{\partial b}[\sum_{i = 1}^N \lambda_i y_i(\omega^Tx_i + b)]
\\ = \frac{\partial}{\partial b}[-\sum_{i = 1}^N \lambda_i y_ib]
\\ = - \sum_{i = 1} ^ N \lambda_i y_i
\]
使结果恒等于 \(0\) , 带入原式:
\[L(\omega, b, \lambda) = \frac{1}{2}\omega^T\omega + \sum_{i = 1}^N\lambda_i - \sum_{i = 1}^N \lambda_iy_i(\omega^Tx_i+b)
\\ = \frac{1}{2}\omega^T\omega + \sum_{i = 1}^N\lambda_i - \sum_{i = 1}^N \lambda_iy_i\omega^Tx_i -\sum_{i = 1}^N \lambda_iy_ib
\\ = \frac{1}{2}\omega^T\omega + \sum_{i = 1}^N\lambda_i - \sum_{i = 1}^N \lambda_iy_i\omega^Tx_i
\]
在对 \(\omega\) 求偏导:
\[\frac{\partial L}{\partial \omega} = \frac{1}{2} · 2 ·\omega - \sum_{i = 1}^N\lambda_i y_i x_i
\]
使结果等于0,求得 \(\omega\):
\[\omega = \sum_{i = 1}^N \lambda_iy_ix_i
\]
那么原式等于:
\[L(\omega, b, \lambda) = - \frac{1}{2} \sum_{i = 1} ^ N \sum_{j = 1} ^ N {\lambda_i \lambda_j y_i y_jx_i^Tx_j} + \sum_{i = 1}^N \lambda_i
\]
最终不等式为:
\[\begin{cases}
max_{\lambda}- \frac{1}{2} \sum_{i = 1} ^ N \sum_{j = 1} ^ N {\lambda_i \lambda_j y_i y_jx_i^Tx_j} + \sum_{i = 1}^N \lambda_i\\
s.t.\quad \lambda_i≥0 、 \sum_{i = 1}^N \lambda_iy_i = 0
\end{cases}
\]
最大化转换程最小化:
\[\begin{cases}
min_{\lambda} \frac{1}{2} \sum_{i = 1} ^ N \sum_{j = 1} ^ N {\lambda_i \lambda_j y_i y_jx_i^Tx_j} - \sum_{i = 1}^N \lambda_i\\
s.t.\quad \lambda_i≥0 、 \sum_{i = 1}^N \lambda_iy_i = 0
\end{cases}
\]
由原问题与对偶问题具有强对偶关系,则满足 \(KKT\) 条件:
\[\begin{cases}\
\frac{\partial L}{\partial \omega} = 0,\frac{\partial L}{\partial b} = 0, \frac{\partial L}{\partial \lambda} = 0
\\
\lambda_i(1 - y_i( \omega^T x_k + b)) = 1\\
\lambda_i ≥ 0\\
1 - y_i(\omega_Tx_i + b) ≤ 0
\end{cases}
\]
求出 \(\omega ^ *、b^*\):
\[\omega^* = \sum_{i = 1}^ N \lambda_i y_i x_i \\
\exists \quad (x_k, y_k) s.t. \quad 1 - y_k(\omega^Tx_k + b) = 0 \\
y_k(w^Tx_k + b) = 1\\
y_k ^ 2(\omega^Tx_k + b) = y_k\\
b^* = y_k - \omega_Tx_k = y_k - \sum_{i = 1} ^ N \lambda_i y_i x_i ^ T x _k
\]
那么最终的超平面:
\[f(x) = sign((\omega^{*})^Tx + b^*)
\]
此时的 \(\omega^*\)是 data 的线性组合

