预训练-Graph Contrastive Learning with Adaptive Augmentation

预训练-Graph Contrastive Learning with Adaptive Augmentation

标签：预训练、图神经网络、对比学习

动机

• 首先，无论是在结构域还是属性域进行简单的数据增强，如 DGI 中的特征移动，都不足以生成不同的邻域，对于节点，特别是在节点特征稀疏的情况下，导致对比目标的优化困难
• 其次，在进行数据增强时，以往的工作忽略了节点和边缘的影响差异。例如，如果我们通过均匀删除边来构造图视图，删除一些有影响的边将会降低嵌入质量
• GCC提出了一个基于CL的预训练框架。提出了基于随机游走的采样子图构造多个增广图，然后采用多种特征工程方案学习模型权值的方法。然而，这些方法没有明确考虑自适应图增强在结构和属性水平。

贡献

• 首先，提出了一个具有强自适应数据增强的无监督图表示学习的一般对比框架。提出的GCA框架在拓扑和属性层次上联合执行数据增强，使模型能够从这两方面学习重要的特征
• 其次，在常用的线性评价协议下，利用5个公共基准数据集对节点分类进行了全面的实证研究。GCA始终优于现有的方法，我们的无监督方法甚至在几个转导任务上超过其有监督的对手

核心思想

数据加强

拓扑结构加强

对于拓扑级扩充，我们考虑一种直接破坏输入图的方法，即随机删除图中的边。形式上，我们用概率从原始的 \(\varepsilon\) 中概率抽取形成新的修改集合 \(\widetilde\varepsilon\)

\[P\{(u,v) \in \widetilde\varepsilon\} = 1 - p_{uv}^e \\ (u, v) \in \varepsilon \\ p_{uv}^e \quad is \quad the \quad probability \quad of \quad removing \quad (u, v) \]

现在的关键是如何计算 \(p_{uv}^e\)， 那么就是通过节点中心性，给出一个节点的中心性 \(\varphi_c(·)\)

则在无向图中定义边中心性则等于两个顶点 \(u, v\) 中心性的平均

\[w_{uv}^e = (\varphi_c(u) + \varphi_c(v)) / 2 \]

在有向图中定义边的中心性为为节点的中心性

\[w_{uv}^e =\varphi_c(v) \]

我们根据每个边缘的中心值计算其概率。由于节点中心度值（如度）可能在数量级上有所不同[29]，因此我们首先设置

\[s_{uv}^e=log(w_{uv}^e) \]

以减轻具有高密度连接的节点的影响。然后，可在将值转换为概率的归一化步骤后获得概率，其定义为

\[p_{uv}^e = min(\frac{s_{max}^e - s_{uv}^e}{s_{max}^e - \mu_{uv}^e} ·p_e, p_{\tau}) \]

\(p_e\) 是控制删除边的总体概率的超参数，\(s_{max}^e\) 和 \(\mu_s^e\) 是 \(s_{uv}^e\) 最大值和平均值, 和\(p_{\tau} < 1\) 是截止概率，用于截断概率，因为极高的移除概率将导致过度损坏的图结构

对于节点中心性函数的选择， 我们使用了以下三种中心性度量

度中心性 : 在无向图中，顶点度就是顶点所连接的边， 在有向图中，顶点的度就是顶点的入边

特征向量中心性 : 与度中心性不同，度中心性假设所有邻居对节点的重要性贡献相等，特征向量中心性也考虑了相邻节点的重要性。根据定义，每个节点的特征向量中心度与其邻居的中心度之和成正比，连接到多个邻居或连接到有影响的节点的节点将具有高的特征向量中心度值。在有向图上，我们使用右特征向量来计算中心性，它对应于引入边。注意，因为只需要前导特征向量，所以计算特征向量中心度的计算负担可以忽略

PageRank中心性: PageRank 中心度定义为由 PageRank 算法计算的 PageRank 权重。该算法沿有向边传播影响，影响最大的节点被视为重要节点。形式上，中心度值定义为

\[\sigma = \alpha AD^{-1}\sigma + 1 \]

其中 \(\sigma \in R^N\) 是每个节点的 PageRank 中心度分数的向量 ，\(\alpha\)是一个阻尼因子，它防止图中的汇吸收来自连接到汇的其他节点的所有等级。我们按照Page等人[30]的建议，设定\(\alpha = 0.85\)。对于无向图，我们在变换的有向图上执行 PageRank，其中每个无向边被转换为两个有向边.

节点级属性加强

我们通过在节点特征中用零随机掩蔽一部分维度来给节点属性添加噪声。形式上，我们首先对随机的向量 \(\widetilde{m} \in \{0, 1\}^F\) 进行采样，它的每个维度独立地从伯努利分布\((1 - p_i^f)\)然后，生成的节点特征由下式计算

\[\widetilde{X} = [x_1 \circ \widetilde{m}; x_2 \circ \widetilde{m}; ···；x_N \circ \widetilde{m}] \]

\(p_i^f\) 的生成首先计算没一个每个维度的权重:

\[w_i^f = \sum_{u\in V} x_{ui} · \varphi_c(u) \\ x_{ui} \in \{0, 1\} \]

类似于拓扑扩充，我们对权重进行归一化以获得表示特征重要性的概率。形式上

\[p_{uv}^e = min(\frac{s_{max}^f - s_{uv}^f}{s_{max}^f - \mu_{uv}^f} ·p_f, p_{\tau}) \\ s_i^f = log (w_i^f) \]

\(s_{max}^f\) 和 \(\mu_s^f\) 是\(s_i^f\) 的最值和平均值

损失函数

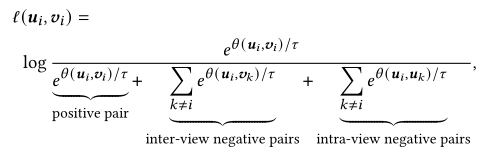
算法框架

1. 采样两个随机增强函数
2. 通过两个随机函数生成两个增强图
3. 通过 GNN 编码获得两个增强图的embedding
4. 计算损失函数
5. 更新参数最大化损失函数

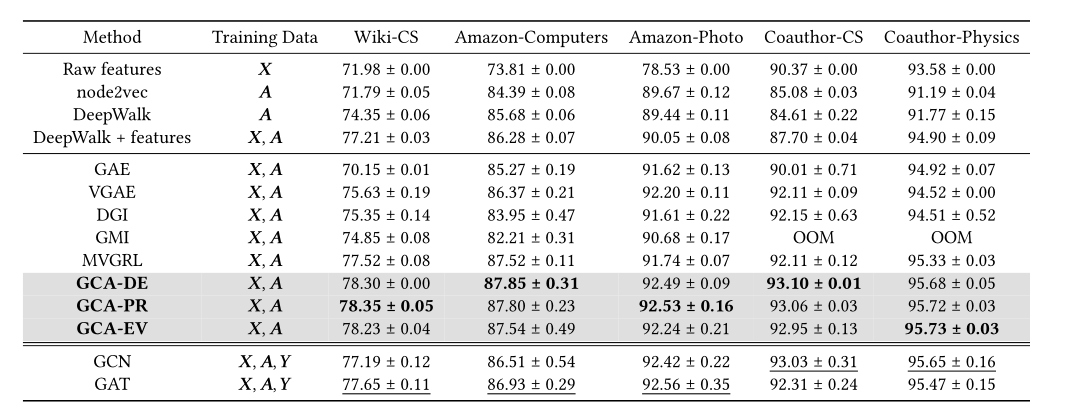
实验结果