BZOJ NOIP提高组十连测第一场
今天的题目一共拿了$180$分，感觉自己还是太菜了，二三两题只能骗到部分分
1、$String\ Master$
题目大意：有两个字符串，在允许k次失配的情况下，求最长公共子串的长度
没什么好讲，直接一个$O(n^3)$的解法就过了，数据范围很小，枚举公共子串在两个字符串的起点，在大于当前字符串长度或在大于$k$次失配后退出，更新答案。
话说卡常后拿了全站$rank1$
$Code\ Below:$
#include <bits/stdc++.h>
using namespace std;
int max(int a,int b){return a>b?a:b;}
int main()
{
register int n,k,ans=0;
char s[310],t[310];
scanf("%d%d\n",&n,&k);
scanf("%s",s);
scanf("%s",t);
for(register int i=0;i<n;i++)
for(register int j=0;j<n;j++){
register int l,cur=0;
for(l=1;i+l<=n&&j+l<=n;l++){
cur+=(s[i+l-1]!=t[j+l-1]);
if(cur>k) break;
}
ans=max(ans,--l);
}
printf("%d\n",ans);
return 0;
}
我的得分：$100$
2、$Tourist\ Attraction$
题目大意:给定点数为$n$的无向图，求经过不重复的$a-b-c-d$的简单路径
$40$分做法：直接深搜
$70$分做法：枚举每一条边的$b-c$，然后$a,d$个数就可以用每个点的度数计算出来，所以$b-c$这条边对答案的贡献为$(dg[a]-1)*(dg[d]-1)$**（想想为什么减一？因为要除去b和c啊）**并减去环的个数
而环的个数恰恰是$70$分解法的瓶颈
$100$分做法：对于$70$分做法，定义所有边终点为$i$的起点集合为$S_i$，其实环的个数就是$card(S_a\cap S_d)$，所以$STL$中冷门数据结构$bitset$就登场了。交集的个数就是两者做与操作后位上$1$的个数
时间复杂度：$O(m*n/32)$
$Code\ Below:$
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn=1500+10;
ll n,dg[maxn],edgex[maxn*maxn],edgey[maxn*maxn],tot,ans;
char s[maxn];
bitset<maxn> t,sum[maxn];
int main()
{
scanf("%lld",&n);
for(ll i=1;i<=n;i++){
getchar();getchar();
for(ll j=1;j<=n;j++){
scanf("%c",&s[j]);
if(s[j]=='1'){
sum[i][j]=1;
edgex[++tot]=i,edgey[tot]=j;
dg[j]++;
}
}
}
for(ll i=1;i<=tot;i++){
ll x=edgex[i],y=edgey[i];
ans+=(dg[x]-1)*(dg[y]-1);
t=sum[x]&sum[y];
ans-=(ll)t.count();
}
printf("%lld\n",ans);
return 0;
}
趁这个机会学了一下$bitset$
我的得分：$40$
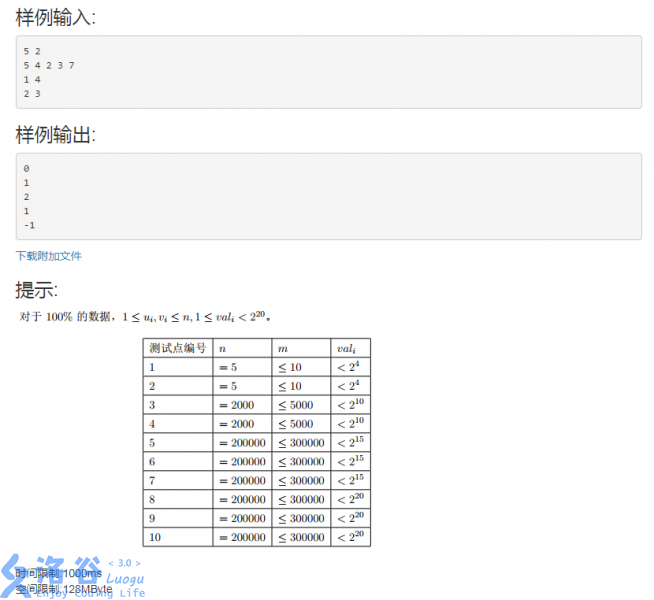
3、$Walk$
题目大意：
$40$分做法：直接$BFS$跑最短路
$Code\ Below:$
#include <bits/stdc++.h>
using namespace std;
int n,m,val[130010<<1],head[1300010<<1],fir[1300010<<1],cnt=1<<20,tot,dis[1300010<<1];
struct node {
int to,next,val;
} e[1300010<<1];
queue<int> q;
inline void add(int x,int y,int w) {
e[++tot].to=y;
e[tot].val=w;
e[tot].next=head[x];
head[x]=tot;
}
inline void add1(int x,int y,int w) {
e[++tot].to=y;
e[tot].val=w;
e[tot].next=fir[x];
fir[x]=tot;
}
void add_point(int x,int dep)
{
if(dis[x]!=-1) return;
dis[x]=dep;q.push(x);
for(int i=head[x];i;i=e[i].next)
add_point(e[i].to,dep);
if(x<=cnt){
for(int i=0;i<=20;i++)
if(x&(1<<i)) add_point(x^(1<<i),dep);
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&val[i]);
add(val[i],i+cnt,0);
add1(i+cnt,val[i],1);
}
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
if(x!=y) add1(x+cnt,y+cnt,1);
}
memset(dis,-1,sizeof(dis));
dis[1+cnt]=0;
while(!q.empty()) q.pop();
memset(dis,-1,sizeof(dis));
dis[1+cnt]=0;q.push(1+cnt);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=fir[u];i;i=e[i].next){
if(dis[e[i].to]==-1){
q.push(e[i].to);
add_point(e[i].to,dis[u]+1);
}
}
}
for(int i=1;i<=n;i++)
printf("%d\n",dis[i+cnt]);
return 0;
}
我的得分：$40$
总结：在攻难题的同时，保证水题正确率$100$%
