二维数组的旋转遍历:顺时针、逆时针和对角线旋转
在面试中,常常会遇到数组的各类旋转问题,例如以顺时针、逆时针或对角线的方式遍历二维数组。这类问题并不涉及算法,只是逻辑有点复杂,一个不小心就会导致访问越界,考验的是编程的基本功。如何优雅地解决此类问题呢?
1. 顺时针旋转
[LeetCode 54. 螺旋矩阵] 给你一个 m 行 n 列的矩阵 matrix ,请按照顺时针螺旋顺序,返回矩阵中的所有元素。
示例 1:
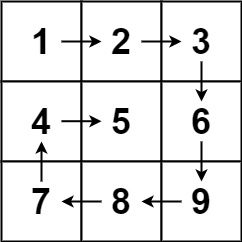
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]示例 2:
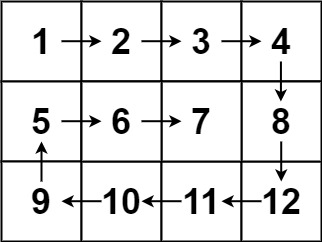
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
仔细观察顺时针旋转的过程,首先顺时针输出矩阵最外面的一圈,随后是第二圈……因此,可以定义函数rotate_one_circle,用于顺时针输出矩阵最外层的一圈,通过在二维数组中左、右、上、下的索引指定矩阵大小。因此,这个函数的原型如下:
// 顺时针旋转矩阵matrix[top:bottom][left:right]最外面的一圈,返回旋转后的结果
vector<int> rotate_one_circle(vector<vector<int>>& matrix, int left, int right, int top, int bottom);利用这个函数,很容易顺时针旋转整个二维数组:
vector<int> rotate(vector<vector<int>>& matrix) {
vector<int> result{};
int m = matrix.size(); // 获取矩阵的第1维大小
if (m == 0) { // 处理输入为空矩阵的情况
return result;
}
int n = matrix[0].size(); // 获取矩阵的第2维大小
int left = 0, right = n-1; // 矩阵的四个边界
int top = 0, bottom = m-1;
for(;left <= right && top <= bottom; left++, right--, top++, bottom--) {
// 每次循环顺时针先遍历矩阵最外层,之后通过修改left,right,top和bottom将矩阵向内收缩一圈
auto v = rotate_one_circle(matrix, left, right, top, bottom);
result.insert(result.end(), v.begin(), v.end());
}
return result;
}现在考虑如何实现旋转一圈的功能:这个很简单,按顺时针方向遍历一圈即可:
vector<int> rotate_one_circle(vector<vector<int>>& matrix, int left, int right, int top, int bottom) {
vector<int> result{};
if (left <= right and top <= bottom) {
for (int j = left; j <= right; j++) {
result.push_back(matrix[top][j]);
}
for (int i = top+1; i <= bottom; i++) {
result.push_back(matrix[i][right]);
}
for (int j = right-1; j >= left; j--) {
result.push_back(matrix[bottom][j]);
}
for (int i = bottom-1; i > top; i--) {
result.push_back(matrix[i][left]);
}
}
return result;
}以上代码对于一般情况是成立的,但对于特殊情况呢?例如left==right或top==bottom的情况?不难发现,对于这样的情况,以上代码存在问题。例如,当left==right时,矩阵退化为一个笔直的长条,如下图所示。图中的1,2,3,4依次表示以上代码中的4个循环,可以看到,第4个循环会再次遍历第2个循环已经遍历过的、长条的中间部分。
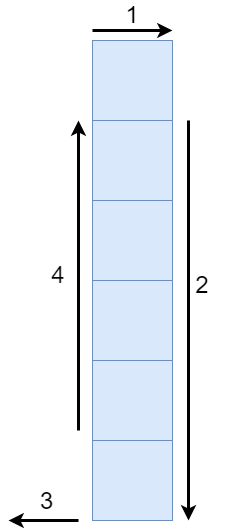
要想解决这个问题,可以直接在代码中分类处理这些特殊情况,也可以直接在上述代码添加控制条件,避免不必要的访问。这里采用后者,修改后的代码如下:
vector<int> rotate_one_circle(vector<vector<int>>& matrix, int left, int right, int top, int bottom) {
vector<int> result{};
if (left <= right and top <= bottom) {
for (int j = left; j <= right; j++) {
result.push_back(matrix[top][j]);
}
for (int i = top+1; i <= bottom; i++) {
result.push_back(matrix[i][right]);
}
if (top < bottom) {
for (int j = right-1; j >= left; j--) {
result.push_back(matrix[bottom][j]);
}
}
if (left < right) {
for (int i = bottom-1; i > top; i--) {
result.push_back(matrix[i][left]);
}
}
}
return result;
}注意,当left==right和top==bottom同时成立时,以上代码也能给出正确结果。
类似的问题还有向二维数组中沿顺时针方向填数,例如59. 螺旋矩阵 II, 2326. 螺旋矩阵 IV. 这类问题本质上还是二维数组的顺时针遍历问题,只需要将以上代码中访问数组元素部分修改为写入数组元素即可。
2. 逆时针旋转
逆时针旋转与顺时针旋转差不多,只不过每次访问最外层时,按照逆时针顺序访问,在此不再赘述。
3. 对角线旋转
[LeetCode 498. 对角线遍历] 给你一个大小为 m x n 的矩阵 mat ,请以对角线遍历的顺序,用一个数组返回这个矩阵中的所有元素。
示例 1:
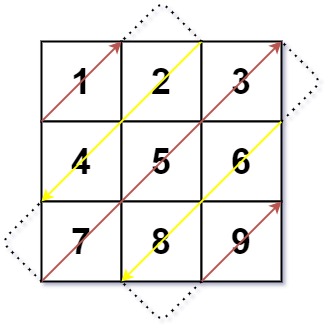
输入:mat = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,4,7,5,3,6,8,9]示例 2:
输入:mat = [[1,2],[3,4]]
输出:[1,2,3,4]
先考虑右边界和下边界不存在的情况,如下图所示:
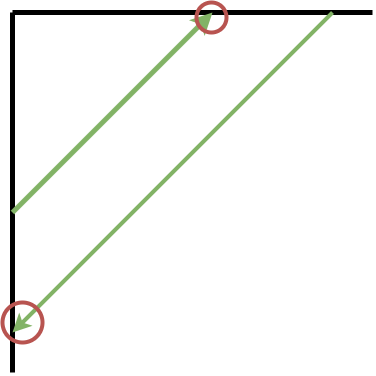
在这种情况下,只有向上运动才会碰到上边界、向下运动才会碰到下边界,并因此改变方向。假设函数next_position计算当前坐标和移动方向下,下一个坐标的位置,此函数的实现如下:
// is_up表示运动的方向,为true时表示向上运动,否则表示向下运动
// 这里传入is_up的引用,因为函数中可能会修改运动方向
vector<int> next_position(int i, int j, bool& is_up) {
if (is_up) {
if (i == 0) { // 向上运动时,碰撞到上边界
is_up = false; // 改变运动方向为向下
return {i, j+1};
}
else {
return {i-1, j+1};
}
}
else {
if (j == 0) { // 向下运动时,碰撞到左边界
is_up = true; // 改变运动方向为向上
return {i+1, j};
}
eles {
return {i+1, j-1};
}
}
}现在,在右侧和下方添加两个边界。不难发现,当向上运动时,在碰到上边界前,可能会先碰到右边界,因此,向上运动时,首先检查是否碰到右边界;向下运动也是同样的道理。
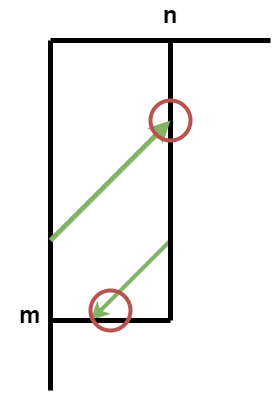
如果m和n分别表示下边界和右边界的位置,函数next_postion的实现如下:
vector<int> next_position(int i, int j, int m, int n, bool& is_up) {
if (is_up) {
if (j == n) { // 向上运动时,碰撞到右边界
is_up = false;
return {i+1, j};
}
else if (i == 0) { // 向上运动时,碰撞到上边界
is_up = false; // 改变运动方向为向下
return {i, j+1};
}
else {
return {i-1, j+1};
}
}
else {
if (i == m) { // 向下运动时,碰撞到下边界
is_up = true;
return {i, j+1};
}
else if (j == 0) { // 向下运动时,碰撞到左边界
is_up = true; // 改变运动方向为向上
return {i+1, j};
}
else {
return {i+1, j-1};
}
}
}有了这个函数,很容易解决上述问题了:
vector<int> visit_diagonal(vector<vector<int>>& mat) {
int i = 0, j = 0;
int m = mat.size(), n = mat[0].size();
bool is_up = true;
vector<int> result {};
for(int k = 1; k <= m*n; k++) { // 访问mxn的二维数组,因此恰好循环mxn次
result.push_back(mat[i][j]);
auto v = next_position(i, j, m-1, n-1, is_up); // 注意,这里右边界和下边界分别为m-1和n-1
i = v[0], j = v[1]; // 更新下一个位置
}
return result;
}


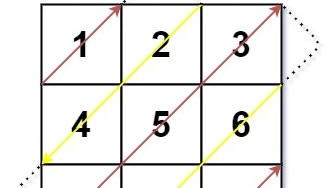 二维矩阵的顺时针、逆时针螺旋遍历,以及对角线遍历.
二维矩阵的顺时针、逆时针螺旋遍历,以及对角线遍历.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号