通过二叉树的前序、中序遍历结果构建二叉树

对于二叉树，我们可以只通过它的前序和中序遍历结果重新构建出二叉树。这听上去很神奇，但其实并不难，下面我们来看看具体是怎么做的吧。

0. 基本原理

对于一棵二叉树，它的前序遍历结果由以下三个部分组成：

[根节点] [左子树的前序遍历结果] [右子树的前序遍历结果]

类似地，它的中序遍历结果由以下三个部分组成：

[左子树的中序遍历结果] [根节点] [右子树的中序遍历结果]

因此，我们首先在前序遍历中找出根节点（即第一个元素），随后根据根节点在中序遍历中的位置将左右子树的中序遍历结果分开，由于左子树的前序和中序遍历结果具有相同的元素个数，可以据此将左右子树的前序遍历结果分开，随后递归构造出这棵二叉树即可。

1. 一个例子

在之前二叉树的遍历一文中，我们使用了这样一棵树：

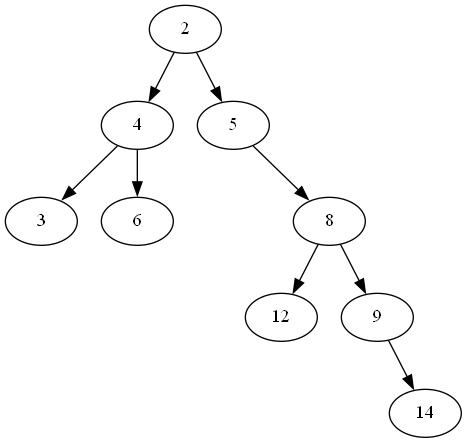
它的前序和中序遍历结果分别为：

(前序): 2 4 3 6 5 8 12 9 14

(中序): 3 4 6 2 5 12 8 9 14

我们首先来看看在这个例子中，如何通过前序和中序遍历的结果构建出二叉树。

首先，前序遍历的第一个数是2，这表明2就是其根节点。我们在中序遍历中找到2这个数字，它左边的一系列数字3 4 6是左子树中的节点, 右边的数字5 12 8 9 14是右子树中的节点。随后我们能够在前序遍历中找到这两个子树的前序遍历结果，也就是4 3 6和5 8 12 9 14. 从而可以看到，可以递归地构建出二叉树。

对于这个例子，大致的过程如下：

build_tree(pre_order, mid_order)  # 通过前序遍历结果pre_order和中序遍历结果mid_order构建二叉树，此函数返回构建的树


build_tree([2 4 3 6 5 8 12 9 14], [3 4 6 2 5 12 8 9 14])
    root = make_node(2)
    root.left = build_tree([4 3 6], [3 4 6])
    root.right = build_tree([5 8 12 9 14], [5 12 8 9 14])
    return root

 2. 代码实现

具体实现时，我们将输入保存在vector中，在函数调用中同时给定需要使用部分的下标索引，从而避免了复制数值时的开销。

二叉树节点的定义如下：

struct BinaryTreeNode {
	int value;
	BinaryTreeNode* lchild;  // left child
	BinaryTreeNode* rchild;  // right child

	BinaryTreeNode(int value, BinaryTreeNode* lchild = nullptr, BinaryTreeNode* rchild = nullptr) {
		this->value = value;
		this->lchild = lchild;
		this->rchild = rchild;
	}
};

以及一个用于新建节点的函数：

BinaryTreeNode* newBinaryTreeNode(int value, BinaryTreeNode* lchild = nullptr, BinaryTreeNode* rchild = nullptr) {
	BinaryTreeNode* node = new BinaryTreeNode(value, lchild=lchild, rchild=rchild);
	return node;
}

 具体的代码实现如下：

BinaryTreeNode* buildTree(const std::vector<int>& preOrder, size_t preStart, size_t preEnd,
	const std::vector<int>& midOrder, size_t midStart, size_t midEnd) {
	// 根据前序遍历结果preOrder[preStart:preEnd]和中序遍历结果midOrder[midStart:midEnd]构建二叉树(包含两个端点)
	if (preStart > preEnd) return nullptr;  // 不存在有效的数据，返回空指针
	else if (preStart == preEnd) {
		// 只有一个元素，新建一个节点并返回
		return newBinaryTreeNode(preOrder[preStart]);
	}
	else {
		int rootValue = preOrder[preStart];  // 根节点是前序遍历的第一个元素
		size_t midIndex = 0;
		for (int i = midStart; i <= midEnd; ++i) {  
			if (midOrder[i] == rootValue) {
				midIndex = i;  // 在中序遍历中找到rootValue
				break;
			}
		}
		// 这样, midOrder[midStart:midIndex-1]和midOrder[midIndex+1:midEnd]就分别是左、右子树的中序遍历结果
		size_t preIndex = preStart + midIndex - midStart;  // 找到左右子树前序遍历结果的分隔处
		BinaryTreeNode* root = newBinaryTreeNode(rootValue);
		root->lchild = buildTree(preOrder, preStart + 1, preIndex,
			midOrder, midStart, midIndex - 1);
		root->rchild = buildTree(preOrder, preIndex + 1, preEnd,
			midOrder, midIndex + 1, midEnd);
		return root;
	}
}

输入测试用例测试下：

int main() {
	std::vector<int> preOrder{ 2, 4, 3, 6, 5, 8, 12, 9, 14 };
	std::vector<int> midOrder{ 3, 4, 6, 2, 5, 12, 8, 9, 14 };
	auto tree = buildTree(preOrder, 0, preOrder.size() - 1,
		midOrder, 0, midOrder.size() - 1);
	levelOrderVisit(tree);  // 按层次遍历打印树
}

输出结果为：

2
4 5
3 6 8
12 9
14