L1范数与L2范数​

L1范数与L2范数​

​ L1范数与L2范数在机器学习中，是常用的两个正则项，都可以防止过拟合的现象。L1范数的正则项优化参数具有稀疏特性，可用于特征选择；L2范数正则项优化的参数较小，具有较好的抗干扰能力。

1. 防止过拟合

​ L2正则项优化目标函数时，一般倾向于构造构造较小参数，一般认为，参数值较小的模型相对简单，能适应不同的数据集，在一定程度上避免过拟合的现象，参数较小，数据偏移带来的影响也会较小，从而说L2正则项具有较好的抗干扰能力，从而实现防止过拟合的现象。

​ L1正则项也可以防止过拟合现象，主要是利用了L1正则项优化参数的稀疏特性。一个简单的模型，配置参数越少，复杂度越小，而稀疏化的参数，模型的的很多参数都变为0，达到减少参数的目的，从而实现防止过拟合的现象。

例子1：

​ 假设有数据点10个数据点，分别为：(0, -2), (10, 18), (20, 15), (30, 35), (40, 42), (50, 50), (60, 66), (70, 76), (80, 77), (90, 85)，如图1（见代码1）。

图1 样例数据点

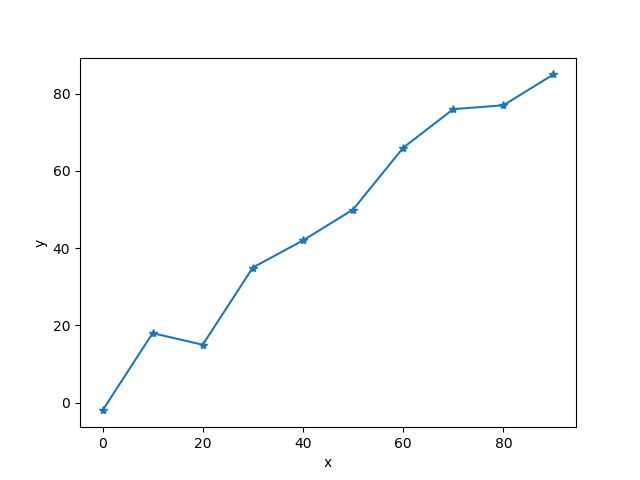
​ 假设该模型为线性模型，即 \(y=ax+b\) 。通过均方误差(MSE)的方式，求解参数\(a\)和\(b\)的值，设上面的10个点分别表示为 \((x_1,y_1),...,(x_{10},y_{10})\) ，目标函数表示为：

\[\begin{align} L &= \sum\limits_{i = 1}^{10} {{{\left( {{y_i} - \left( {a{x_i} + b} \right)} \right)}^2}} \nonumber\\ &= \left( {Y - AX} \right){\left( {Y - AX} \right)^T} \end{align} \]

其中，\(Y = \left( {{y_1},...,{y_N}} \right) \in {R^{1 \times N}}​\)，\(A = \left( {a,b} \right) \in {R^{1 \times 2}}​\)，\(X = \left( {\begin{array}{*{20}{c}} {{x_1}}& \cdots &{{x_N}}\\ 1& \cdots &1 \end{array}} \right) \in {R^{1 \times N}}​\)。

求解：

\[\frac{{\partial L}}{{\partial A}} = 2\left( {Y{X^T} - AX{X^T}} \right) = 0 \\ A = Y{X^T}{\left( {X{X^T}} \right)^{ - 1}} \\ A = \left( {\begin{array}{*{20}{c}} {0.971}&{{\rm{2}}{\rm{.509}}} \end{array}} \right) \]

（结果见代码1）。

添加L2正则项，

\[L = \left( {Y - AX} \right){\left( {Y - AX} \right)^T} + {\left\| A \right\|^2} \]

求解得到

\[A = Y{X^T}{\left( {I + X{X^T}} \right)^{ - 1}} \\ A = \left( {\begin{array}{*{20}{c}} {{\rm{0}}{\rm{.985}}}&{{\rm{1}}{\rm{.623}}} \end{array}} \right) \]

（结果见代码2）。

# 代码1
import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import inv
if __name__ == '__main__':
    x = np.arange(0, 100, 10)
    np.random.seed(2019)
    y = x + np.random.randint(-10, 11, 10)
    data = list(zip(x, y))
    print(data)  
    # [(0, -2), (10, 18), (20, 15), (30, 35), (40, 42), (50, 50), (60, 66), 
    # (70, 76), (80, 77), (90, 85)]
    plt.plot(x, y, '-*')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.show()
    X = np.vstack((np.array(x), np.ones(len(x))))
    Y = np.array(y)
    A = Y.dot(X.T).dot(inv(X.dot(X.T)))
    print(A)  # [0.97090909 2.50909091]

2. L1正则化的稀疏解释

首先阐述一下为什么需要稀疏。

假设有样本\(x \in R^m\), \(X=(x_1,...,x_N)\)是\(N\)个样本，\(x_i\)是列向量，这\(N\)个样本的类别表示为\(Y=(y_1,...,y_N)\)，假设\(m>N\)，现有一个线性模型\(Y=\theta X\), \(\theta \in R^m\), 由于\(m>N\)，所以$ \theta $ 有无数个解，\(x_i\) 是 \(m\) 维的列向量，可能并不是所有的属性对构建模型都是有效的，此时需要筛选出一些有用的属。这里对于无用的属性，可以使用 $ \theta $ 筛选，在指定位置置零即可，除掉 \(X\) 中无用的属性，此时可能有 \(m_{new} < N\) 该线性模型可能得到唯一解。但是，如何寻找稀疏的 $ \theta $ 呢？

参考：https://vimsky.com/article/3852.html

​

​

​