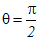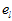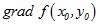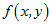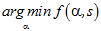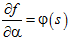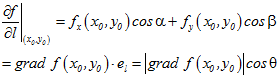梯度下降法

梯度下降法的计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）。

其一般 迭代公式步骤如下：

目标函数：

梯度：

迭代公式

（沿着负梯度方向前进，值下降最快）

 

--------------------------------------------------------------------------------------

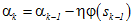
补充：梯度（高等数学）

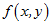
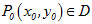
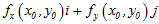
    在二元函数的情形，设函数 在平面区域D内具有一阶连续偏导数，则对于没一点 ，都可以定出一个向量：

，

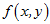
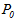
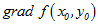
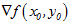
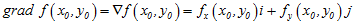
这向量成为函数在点的梯度，记作 或者 。

，

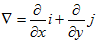
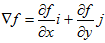
其中 称谓二维的向量微分算子或者Nabla算子，

。

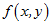
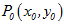
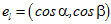
    如果函数 在点可微分， 是与方向 同向的单位向量，则

其中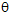 表示梯度方向与 方向之间的夹角。

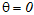
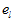
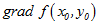
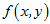
    （1）当 ，即方向 与梯度 的方向相同时，函数增加最快；

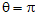
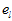
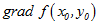
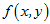
    （2）当 ，即方向 与梯度 的方向相反时，函数减少最快；

    （3）当 ，即方向 与梯度 的方向正交时，函数变化率为0。