树与二叉树
知识框架

树的基本概念
1.树的定义
树是n(n ≥ 0)个结点的有限集合,n = 0时,称为空树,这是一种特殊情况。在任意一颗非空树中应满足:
1)有且只有一个特定的称为根的结点
2)当n > 1时,其余结点可分为m(m > 0)个互不相交的有限集合T1,T2,···,Tm,其中每个集合本身又是一棵树,并且称为根节点的子树。
显然,树的定义是递归的,是一种递归的数据结构。树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
1)树的根结点没有前驱结点,除根结点外的所有结点 有且只有一个前驱结点
2)树中所有结点可以有零个或多个后继特点
树适用于表示具有层次结构的数据。树中的某个结点(除根结点外)最多只和上一层的一个结点(即父结点)有直接关系,根结点没有直接上层结点,因此在n个结点的树中有n-1条边。而树中每个结点与其下一层的零个或多个结点(即其子女结点)有直接关系。
2.树的基本性质
1)树中的结点数等于所有结点的度数+1
2)度为m的树中第i层上至多有mi-1个结点(i ≥ 1)
3)高度为h的m叉树至多有(mh-1)/(m-1)个结点
4)具有n个结点的m叉树的最小高度为 ⌈ logm(n(m-1) + 1) ⌉
二叉树的概念
1.二叉树的定义
二叉树是另一种树形结构,其特点是每个结点至多只有两颗子树(即二叉树中不存在度大于2的结点),并且二叉树的子树有左右之分,其次序不能任意颠倒。
与数相似,二叉树也以递归的形式定义。二叉树是n(n≥0)个结点的有限集合:
1.或者为空二叉树,即n=0。
2.或者由一个根节点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一颗二叉树。
二叉树是有序树,若将其左子树、右子树颠倒,则成为另一颗不同的二叉树。即时树中结点只有一颗子树,也要区分它是左子树还是右子树。二叉树的五种基本形态:
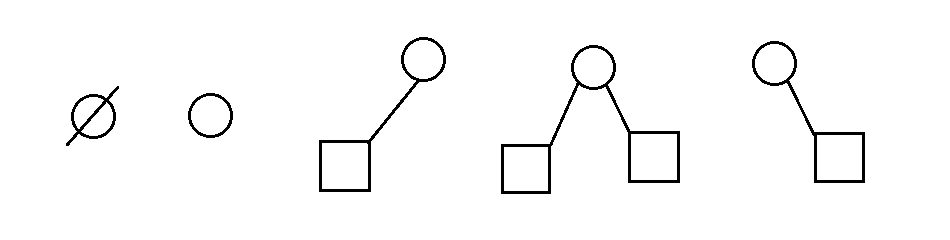
二叉树与度为2的有序树的区别:
1.度为2的树至少有3个结点,而二叉树可以为空。
2.度为2的有序树的孩子结点的左右次序是相对于另一孩子结点而言的,若某个结点只有一个孩子结点,则这个孩子结点就无须区分左右次序,而二叉树无论其孩子树是否为2,均需确定其左右次序,即二叉树的结点次序不是相对于另一结点而言,而是确定的。
2.几个特殊的二叉树
1)满二叉树
一颗高度为h,并且含有2h -1个结点的二叉树称为满二叉树,即树中的每层都含有最多的结点。满二叉树的叶子结点都集中在在二叉树的最下层,并且除了叶子结点之外的每个结点度数都是2。
可以这么对满二叉树按层序编号:从根节点(根节点编号为1)开始,从上到下,从左到右。这样每个结点对应一个编号,对于编号为i 的结点,若有双亲,则其双亲为⌊i/2⌋,若有左孩子则左孩子为2i ;若有右孩子,则右孩子为2i + 1。
2)完全二叉树
设一个高度为h、有n个结点的二叉树,当且仅当其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应,称为 完全二叉树。这种树的特点如下:
1.若 i ≤ ⌊n/2⌋,则结点i 为分支结点,否则为叶子结点。
2.叶子结点只可能在层次最大的两层上出现。对于最大层次中的叶子结点,都依次排列在该层的最左边的位置上。
3.若有度为1 的结点,则只可能有一个,且该结点只有左孩子而无右孩子(重要特征)。
4.按层序编号后,一旦出现某结点(编号为i)为叶子结点或只有左孩子,则编号大于i的结点均为叶子结点。
5.若n为奇数,则每个分支结点都有左子女和右子女;若n为偶数,则编号最大的分支结点(编号为n/2)只有左子女,没有右子女,其余分支结点左、右子女都有。
3)二叉排序树
一颗二叉树或者是空二叉树,或者是具有如下性质的二叉树:
左子树上所有结点的关键字均小于根节点的关键字;
右子树上所有结点的关键字均大于根节点的关键字。
则左子树和右子树又各是一颗二叉排序树。
4)平衡二叉树
树上任一结点的左子树和右子树的深度之差不超过1。
3.二叉树的性质
1)非空二叉树上的叶子结点数等于度为2的结点数加1,即 n0 = n2 +1。
2)非空二叉树上第k层上至多有 2k-1个结点(k ≥1)。
3)高度为h的二叉树至多有 2h - 1个结点(h ≥ 1)。即是满二叉树状态
4)对完全二叉树按从上到下、从左到右的顺序依次编号为1,2,3,...,n,则有以下关系:
1.当 i > 1时,结点i 的双亲结点编号为⌊i/2⌋,即当i 为偶数时,其双亲结点的编号为 i/2,它是双亲结点的左孩子;当i为奇数时,其双亲结点的编号为(i-1)/2 ,它是双亲结点的右孩子。
2.当2i ≤ n时,结点i 的左孩子编号为 2i ,否则无左孩子。
3.当 2i + 1 ≤ n 时,结点i 的右孩子为 2i+1,否则无右孩子。
4.结点i 所在层次(深度)为⌊log2i⌋ + 1。
5)具有n个(n > 0)结点的完全二叉树的高度为 ⌈log2(n+1)⌉ 或 ⌊log2n⌋ + 1。
二叉树的存储方式
1.顺序存储结构
二叉树的顺序存储就是用一组地址连续的存储单元依次从上而下、从左至右存储完全二叉树上的结点元素。
依据二叉树的性质,完全二叉树和满二叉树采用顺序存储比较合适。
2.链式存储结构
由于顺序存储的空间利用率低,因此二叉树一般都采用链式存储结构。链式结构是指用一个链表来存储一颗二叉树,二叉树中的每个结点用链表的一个链结点来存储。

typedef struct BiTNode{ ElemType data; //数据域 struct BiTNde *lchild, *rchild; //左孩子右孩子指针 }
使用不同的存储结构时,实现二叉树操作的算法也不同,因此要根据实际应用场合来选择合适的存储结构。
二叉树的遍历
所谓二叉树的遍历,是指按某条搜索路径访问树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。
1.先序遍历
先序遍历(PreOrder)的操作过程:
若二叉树为空,则什么也不做;否则,
1)访问根结点;
2)先序遍历左子树;
3)先序遍历右子树。
对应的递归遍历如下:
1 2 3 4 5 6 7 | void PreOrder(BiTree T) { if (T != NULL) { visit(T); //访问根结点 PreOrder(T->lchild); //递归遍历左子树 PreOrder(T->rchild); //递归遍历右子树 }} |
2.中序遍历
中序遍历(InOrder)的操作过程如下:
若二叉树为空,则什么也不做;否则,
1)中序遍历左子树;
2)访问根结点;
3)中序遍历右子树。
对应的递归算法如下:
1 2 3 4 5 6 7 | void InOrder(BiTree T) { if (T != NULL) { PreOrder(T->lchild); //递归遍历左子树 visit(T); //访问根结点 PreOrder(T->rchild); //递归遍历右子树 }} |
3.后序遍历
后序遍历(PostOrder)的操作过程如下:
若二叉树为空,则什么也不做;否则,
1)后序遍历左子树;
2)后序遍历右子树;
3)访问根结点。
对应的递归算法如下:
1 2 3 4 5 6 7 | void PostOrder(BiTree T) { if (T != NULL) { PreOrder(T->lchild); //递归遍历左子树 PreOrder(T->rchild); //递归遍历右子树 visit(T); //访问根结点 }} |
4.递归算法和非递归算法的转换
借助栈,可以将二叉树的递归遍历算法转换为非递归算法。
1)中序遍历的非递归算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | void InOrder2(BiTree T){ //二叉树中序遍历的非递归算法,算法需要借助一个栈 InitStack(S); BiTree p = T; //初始化栈;p是遍历指针 while (p || !IsEmpty(S)) { //栈不空或p不空时循环 if (p) { //根指针入栈,遍历左子树 Push(S, p); //每遇到非空二叉树向左走 p = =->lchild; } else { //根指针退栈,访问根结点,遍历右子树 Pop(S, p); visit(p); //退栈,访问根结点 p = p->rchild; //再向右子树走 } }} |
2)层序遍历

要进行层次遍历,需要借助一个队列。先将二叉树根结点入队,然后出队,访问该结点,若它有左子树,则将左子树根结点入队;若它有右子树,则将右子树根结点入队。然后出队,对出队结点访问,如此反复,直到队列为空。
二叉树的层次遍历算法如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 | void LevelOrder(BiTree T) { InitQueue(Q); //初始化辅助队列 BiTree p; EnQueue(Q, T); //将根结点入队 while (!IsEmpty(Q)) { //队列不空循环 DeQueue(Q, p); //队头元素出队 visit(p); //访问当前p所指向结点 if (p->lchild != NULL) //左子树不空,则左子树入队列 EnQueue(Q, p->lchild); if (p->rchild != NULL) //右子树不空,则右子树入队列 EnQueue(Q, p->rchild); }} |
5.由遍历序列构造二叉树
由二叉树的先序序列和中序序列可以唯一的确定一颗二叉树。 在先序遍历序列中,第一个结点一定是二叉树的根结点;而在中序遍历中,根结点必然将中序序列分割成两个子序列,前一个子序列是根结点的左子树的中序序列,后一个子序列是根结点的右子树的中序序列。根据这两个子序列,在先序序列中找到对应的左子序列和右子序列。在先序序列中,左子序列的第一个结点是左子树的根结点,右子序列的第一个结点是右子树的根结点。如此递归下去,便能唯一的确定这颗二叉树。
同理,由二叉树的后序序列和中序序列也能唯一的确定一颗二叉树。因为后序序列的最后一个结点就如同先序序列的第一个结点,可以将中序序列分割成两个子序列,然后采用类似的方法递归的进行划分,进而得到一颗二叉树。
由二叉树的层序序列和中序序列也可以唯一的确定一颗二叉树,实现方法类似。
注意:只知道二叉树的先序序列和后序序列是无法确定一颗二叉树的。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
2017-05-19 快速幂