浮点数:A Programmer's Perspective
Maybe you asked for help on some forum and got pointed to a long article with lots of formulas that didn’t seem to help with your problem。Then this article may do a little favor.
—— 前注。嗯,我这里指的就是Oracle和Stack Overflow
1.问题来源
近日在《程序员面试宝典》中看到一道类型装换的题目,关于浮点数float型装换为int&类型时,输出结果是什么?代码如下
#include <iostream>
using namespace std;
int main()
{
float a = 1.0f;
cout<< (int) a <<endl;
cout << &a << endl;
cout << (int&)a << endl;
cout << boolalpha << ( (int)a == (int&)a ) <<endl;
float b = 0.0f;
cout<< (int) b <<endl;
cout << &b << endl;
cout << (int&)b << endl;
cout << boolalpha << ( (int)b == (int&)b ) <<endl;
return 0;
}
using namespace std;
int main()
{
float a = 1.0f;
cout<< (int) a <<endl;
cout << &a << endl;
cout << (int&)a << endl;
cout << boolalpha << ( (int)a == (int&)a ) <<endl;
float b = 0.0f;
cout<< (int) b <<endl;
cout << &b << endl;
cout << (int&)b << endl;
cout << boolalpha << ( (int)b == (int&)b ) <<endl;
return 0;
}
g++编译运行结果如下:
1
0x22ff3c
1065353216
false
0
0x22ff38
0
true
请按任意键继续. . .
0x22ff3c
1065353216
false
0
0x22ff38
0
true
请按任意键继续. . .
1.0f是如何转换成了1065353216?
要回答这个问题首先得了解IEEE制定的“浮点表示法”
2.浮点数基础知识
| Name | Common name | Base | Digits | E min | E max | Notes | Decimal digits | Decimal E max |
|---|---|---|---|---|---|---|---|---|
| binary16 | Half precision | 2 | 10+1 | −14 | +15 | storage, not basic | 3.31 | 4.51 |
| binary32 | Single precision | 2 | 23+1 | −126 | +127 | 7.22 | 38.23 | |
| binary64 | Double precision | 2 | 52+1 | −1022 | +1023 | 15.95 | 307.95 | |
| binary128 | Quadruple precision | 2 | 112+1 | −16382 | +16383 | 34.02 | 4931.77 | |
| decimal32 | 10 | 7 | −95 | +96 | storage, not basic | 7 | 96 | |
| decimal64 | 10 | 16 | −383 | +384 | 16 | 384 | ||
| decimal128 | 10 | 34 | −6143 | +6144 | 34 | 6144 |
表1 浮点数结构表
我们这里只讨论float类型,即上面的binary32,这是单精度的二进制浮点数,共有24位,结构为:

图1 32位float类型浮点数的结构图
其中,s为符号位 signed/unsigned,exp为指数位 exponent,frac为分数前缀。
需要注意的是,由于Intel CPU的架构是Little Endian(具体参见计算机原理相关知识),一个32位的float数据将其分为 A,B,C,D 四段,那么在小端法机器中实际存储结构为 DCBA。本篇文章中先不考虑小端法表示,直接用我们比较熟悉的高位在前表示法进行讨论,需要切换成小端法结构,再倒序排列。
计算机中的“浮点计数法”实际上就是科学计数法的2进制版本。我们可以用十进制的转换来类比二进制浮点数的处理。
整数部分:整数的十进制数和二进制数可以一位一位地看| Decimal (base 10) | Binary (base 2) | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ⋅ | 101 | + | 3 | ⋅ | 100 | = | 1310 | = | 11012 | = | 1 | ⋅ | 23 | + | 1 | ⋅ | 22 | + | 0 | ⋅ | 21 | + | 1 | ⋅ | 20 |
| 1 | ⋅ | 10 | + | 3 | ⋅ | 1 | = | 1310 | = | 11012 | = | 1 | ⋅ | 8 | + | 1 | ⋅ | 4 | + | 0 | ⋅ | 2 | + | 1 | ⋅ | 1 |
表2 整数表示法列表
小
数部分:那么,小数的十进制数和二进制数同样地也可以一位一位地看。
| Decimal (base 10) | Binary (base 2) | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | ⋅ | 10-1 | + | 2 | ⋅ | 10-2 | + | 5 | ⋅ | 10-3 | = | 0.62510 | = | 0.1012 | = | 1 | ⋅ | 2-1 | + | 0 | ⋅ | 2-2 | + | 1 | ⋅ | 2-3 |
| 6 | ⋅ | 1/10 | + | 2 | ⋅ | 1/100 | + | 5 | ⋅ | 1/1000 | = | 0.62510 | = | 0.1012 | = | 1 | ⋅ | 1/2 | + | 0 | ⋅ | 1/4 | + | 1 | ⋅ | 1/8 |
表3 小数表示法列表
至于十进制的科学数如何转换为二进制下的科学数,可以需要分成整数和小数两个部分,如下图以244.975来说明,整数244采用“除16取余,逆序排列”的方法,连续取余数,直到余数为0,然后逆序排列余数,即得到相应的16进制数,再由16进制数转换为2进制数就很简单了;而小数部分0.975则是采用“乘16取余,顺序排列”的方法,乘以16,将整数余下,对剩余小数部分重复这一过程,直至出现相同的小数或者0则终止,然后按正序排列余下的整数,即得到小数部分的相应的16进制数,再由16进制数转换为2进制数。最后,组合两部分,就完成了整个装换。

图2.十进制数到二进制数的转换过程(以244.975为例)
3.如何转换得到浮点数
十进制的小数转换为二进制的小数,还没有达到我们的最终目的,我们要得到的是float格式的数据。下面真正进入浮点数转换过程。再次强调,浮点数其实就是二进制下的归一化科学计数法“Scientific Notation”。十进制下Scientific Notation为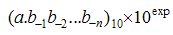 ,那么二进制下的Normalized Scientific Notation即为
,那么二进制下的Normalized Scientific Notation即为 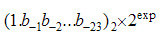 在上面的公式上做一个很小的变化就可以得到二进制浮点数的表达公式,如下:
在上面的公式上做一个很小的变化就可以得到二进制浮点数的表达公式,如下:
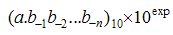 ,那么二进制下的Normalized Scientific Notation即为
,那么二进制下的Normalized Scientific Notation即为 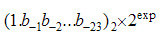 在上面的公式上做一个很小的变化就可以得到二进制浮点数的表达公式,如下:
在上面的公式上做一个很小的变化就可以得到二进制浮点数的表达公式,如下: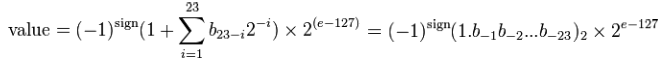
相应的变化就是8 bits的指数部分exponent,变为e-127,这是因为正常的八位只能表示 0 → 255,而实际上归一化的科学计数指数有正有负,所以统一地用e-127,理论上可以表示 -127 → 128 的指数范围。但IEEE 754 standard做了如下的限定:
- Emin = 01H−7FH = −126
- Emax = FEH−7FH = 127
- Exponent bias = 7FH = 127
所以归一化的指数范围为 -126 → 127 ,Exponent的另外两种00 FF的意义如下:
| Exponent |
Significand zero
| Significand non-zero | Equation |
|---|---|---|---|
| 00H | zero, −0 |
非归一化数
|
(−1)signbits×2−126× 0.significandbits |
| 01H, ..., FEH | normalized value | (−1)signbits×2exponentbits−127× 1.significandbits | |
| FFH | ±infinity无穷 | NaN (quiet, signalling) | |
表4 浮点数指数及表达式表
其中,Significand为计数法中的前缀数,Significand zero表示前缀数为0。
0.15625f先将十进制小数转换为二进制形式的小数:(0.00101)2 =(1.01)2*2-3.
填写各个bit。
- 第31位sign,符号位为正:0
- 第30-23位,exp指数位,e=127+(-3)=124: 01111100
- 第22-0位,分数部分,(1.01)2去掉1和小数点,直接填:01(补满23位)

图3.浮点数的表示法(以0.15625为例)
至此,我们页首的问题也就解决了。
1.0f = (1.0)2*20. s = 0 , e = 127 = 0111 1111 , frac = 0
所以存储的数为 (3F 80 00 00)16 = 1065353216
题目中float a=1.0f,强制转换为(int&),int型引用,会输出int型引用类型赋值(a)的位置开始sizeof(int)大小的数,即1065353216,
float b=0.0f,为(−1)signbits×2−126× 0.significandbits = (−1)0×2−126× 0.0 ,这个位置存储的数还是0。
4.Problems
通过上面的转换,我们可以看出一个问题:只有被除数是2的指数得出的有限小数,才能用二进制有限小数表示。这样造成的结果是,我们在十进制下能很好表示的有限小数如0.1,到了二进制小数下就成了无限循环小数,用无限循环小数的表示必然涉及到 rounding errors。
|
Fraction
分数
|
Base
基数
| Positional Notation |
Rounded to 4 digits
估读为4位
|
Rounded value as fraction
估读值对应的分数
|
Rounding error
估读误差
|
|---|---|---|---|---|---|
| 1/10 | 10 | 0.1 | 0.1 | 1/10 | 0 |
| 1/3 | 10 | 0.3 | 0.3333 | 3333/10000 | 1/30000 |
| 1/2 | 2 | 0.1 | 0.1 | 1/2 | 0 |
| 1/10 | 2 | 0.00011 | 0.0001 | 1/16 | 3/80 |
这就是为什么有时候一个简单的加法
0.1 + 0.2
却得到一个看似荒唐的结果
0.30000000000000004
下面简要介绍几种舍入误差“Round Error”下产生的错误。
(1).浮点数相等判断
由于十进制到二进制本身就有round error,在这个基础要判断两个float数相等就容易出
float a = 0.15 + 0.15
float b = 0.1 + 0.2
if(a == b) // can be false!
if(a >= b) // can also be false!
float b = 0.1 + 0.2
if(a == b) // can be false!
if(a >= b) // can also be false!
(2).不要用绝对误差absolute error margins
if( Math.abs(a-b) < 0.00001) // wrong - don't do this
if( Math.abs((a-b)/b) < 0.00001 ) // still not right!
(3).浮点数的边缘检测的注意点
Look out for edge cases
There are some important special cases where this will fail:
- When both a and b are zero. 0.0/0.0 is “not a number”, which causes an exception on some platforms, or returns false for all comparisons.
- When only b is zero, the division yields “infinity”, which may also cause an exception, or is greater than epsilon even when a is smaller.
- It returns false when both a and b are very small but on opposite sides of zero, even when they’re the smallest possible non-zero numbers.
以及一个可行的检测程序:
public static boolean nearlyEqual(float a, float b, float epsilon)
{
final float absA = Math.abs(a);
final float absB = Math.abs(b);
final float diff = Math.abs(a - b);
if (a == b)
final float absA = Math.abs(a);
final float absB = Math.abs(b);
final float diff = Math.abs(a - b);
if (a == b)
{ // shortcut, handles infinities
return true;
}
return true;
}
else if (a == 0 || b == 0 || diff < Float.MIN_NORMAL)
{// a or b is zero or both are extremely close to it
// relative error is less meaningful here
// relative error is less meaningful here
return diff < (epsilon * Float.MIN_NORMAL);
}
}
else
{ // use relative error
return diff / (absA + absB) < epsilon;
}
}
return diff / (absA + absB) < epsilon;
}
}
Reference:

