第十届蓝桥杯大赛软件类省赛研究生组 试题D:最短路

第十届蓝桥杯大赛软件类省赛研究生组 试题D:最短路

试题描述

如下图所示，G是一个无向图，其中蓝色边的长度是1、橘色边的长度是2、绿色边的长度是3。

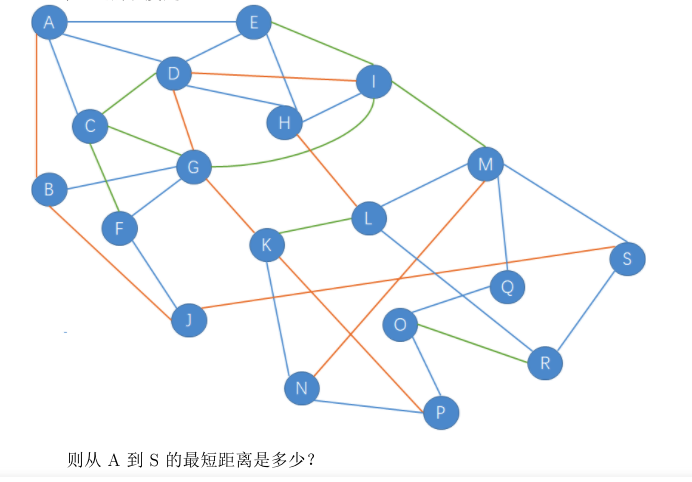
此题不能直接上Dijkstra或者其他的最短路径算法。作为考试，要从图入手，很容易可以看出最短路径为6（A->B->J->S 或者其他路径）

如果碰到很难看出的图，要用最短路径算法。

Dijkstra通用C/C++模版

#include <bits/stdc++.h>
using namespace std;

const int max_num = 100;
const int max_int = 9999;

void Dijkstra(int n, int v, int *dist, int *prev, int c[max_num][max_num]){
    bool s[max_num]; // 判断是否加入s集合
    for(int i = 1;i <= n;i++){
        s[i] = false;
        dist[i] = c[v][i];
        if(dist[i] == max_int)
            prev[i] = 0;
        else
            prev[i] = v;
    }
    dist[v] = 0;
    s[v] = true;

    for(int i = 2;i <= n ;i++){
        int min_value = max_int;
        int u = v;
        for(int j = 1;j <= n;j++){
            if(!s[j] && dist[j] < min_value){
                u = j;
                min_value = dist[j];
            }
        }

        s[u] = true; // 将选出的最小权值的定点加入s

        //更新path
        for(int j = 1;j <= n;j++){
            if(!s[j] && c[u][j] < max_int){
                if(dist[u] + c[u][j] < dist[j]){
                    dist[j] = dist[u] + c[u][j];
                    prev[j] = u;
                }
            }
        }
    }
}

void search_path(int *prev, int u, int v){
    int loc_queue[max_num], count = 1;
    loc_queue[count++] = v;
    int prev_loc = prev[v];
    while(prev_loc != u){
        loc_queue[count++] = prev_loc;
        prev_loc = prev[prev_loc];
    }
    loc_queue[count] = u;

    // 打印数组
    while (count >= 1){
        if(count != 1)
            cout << loc_queue[count--] << " --> ";
        else
            cout << loc_queue[count--];
    }

}

main 函数

int main(int argc,char * argv[]){

    int dist[max_num];
    int prev[max_num];
    int c[max_num][max_num];
    int n, edge_count; //图的节点数和路经数
    int u, v, weight;

    cin >> n >> edge_count;
    for(int i = 1;i <= n; i++)
        for (int j = 1; j <= n ; ++j)
            c[i][j] = max_int;
    //初始化图
    for(int i = 1;i <= edge_count;i++){
        cin >> u >> v >> weight;
        if (weight < max_int){
            c[u][v] = weight;
            c[v][u] = weight;
        }
    }

    for(int i = 1;i <= edge_count;i++){
        dist[i] = max_int;
    }
    cout << endl;

    // 打印输入数据
    for (int i = 1; i <=n ; ++i) {
        for (int j = 1; j <= n; ++j)
            printf("%8d", c[i][j]);
        cout << endl;
    }

    Dijkstra1(n, 1, dist, prev, c);
    printf("原点到最后一点的距离为：%d\n",dist[n]);
    cout << "路径为：" << endl;
    search_path1(prev, 1, n);

    return 0;
}

输入点集合

19 35
1 2 2
1 3 1
1 4 1
1 5 1
2 7 1
2 10 2
3 6 3
3 4 3
3 7 3
4 5 1
4 7 2
4 8 1
4 9 2
5 8 1
5 9 3
6 7 1
6 10 1
7 11 2
7 9 3
8 9 1
8 12 2
9 13 3
10 19 2
11 14 1
11 12 3
11 16 2
12 18 1
12 13 1
13 14 2
13 17 1
13 19 1
14 16 1
15 16 1
15 17 1
15 18 3
18 19 1

.....数据找的头秃