【BFS和DFS的性质】[NOI2013]树的计数

题目描述

我们知道一棵有根树可以进行深度优先遍历（DFS）以及广度优先遍历（BFS）来生成这棵树的 DFS 序以及 BFS 序。两棵不同的树的 DFS 序有可能相同，并且它们的 BFS 序也有可能相同，例如下面两棵树的 DFS 序都是 1 2 4 5 3，BFS 序都是 1 2 3 4 5。

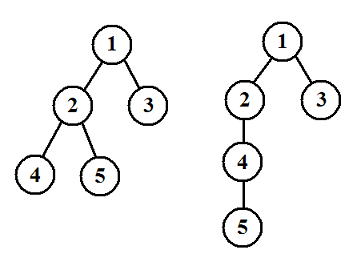
现给定一个 DFS 序和 BFS 序，我们想要知道，符合条件的有根树中，树的高度的平均值。即，假如共有 K 棵不同的有根树具有这组 DFS 序和 BFS 序，且他们的高度分别是 h1,h2,…,hK，那么请你输出：

h1+h2+⋯+hKK

输入格式

第一行包含 1 个正整数 n，表示树的节点个数。

第二行包含 n 个正整数，是一个 1∼n 的排列，表示树的 DFS 序。

第三行包含 n 个正整数，是一个 1∼n 的排列，表示树的 BFS 序。

输入保证至少存在一棵树符合给定的两个序列。

输出格式

仅包含 1 个实数，四舍五入保留恰好三位小数，表示树高的平均值。

样例一

input

5 
1 2 4 5 3 
1 2 3 4 5

output

3.500

限制与约定

如果输出文件的答案与标准输出的差不超过 10−3，则将获得该测试点上的分数，否则不得分。

20% 的测试数据，满足：n≤10；

40% 的测试数据，满足：n≤100；

85% 的测试数据，满足：n≤2000；

100% 的测试数据，满足：2≤n≤200000。

时间限制：1s

空间限制：256MB

说明

树的高度：一棵有根树如果只包含一个根节点，那么它的高度为 1。否则，它的高度为根节点的所有子树的高度的最大值加 1。

对于树中任意的三个节点 a,b,c，如果 a,b 都是 c 的儿子，则 a,b 在 BFS 序中和 DFS 序中的相对前后位置是一致的，即要么 a 都在 b 的前方，要么 a 都在 b 的后方。

分析

我们将BFS序列改为1…n，对应的也修改dfs序的标号。
令pos[i]表示bfs序为i的节点在dfs序中的位置。
然后我们要做的就会要对bfs序分层。
每一种分层对应几种满足dfs序的方案呢？

这相当于问子节点到父节点有几种连法。
在两种不同连法中，父1,父2,子 的相对顺序不同，所以只有一种符合DFS序。

所以一种划分只对应一棵树。

然后我们来看看应该应该怎么分层。

BFS序性质

首先，考虑一下同一层的点应该满足的条件

令这一层的节点为[l,r]

1. pos[i]<pos[i+1]  i∈[l,r)，这个性质很显然，因为dfs和bfs都是遍历一个节点的领接边的顺序是一样的。
2. 1号节点必须单独成层。

DFS序性质

我们再来看看dfs序的性质，假设dfs序为d[1]…d[n]

• dep[d[i]]+1>=dep[d[i+1]]，因为d[i+1]要么是d[i]的第一个儿子(dep[d[i]]+1=dep[d[i+1]])，要么是d[i]没有儿子， 之后访问到的是d[i+1](dep[d[i]]>=dep[d[i+1]]).

分层

令x[i]表示i和i+1节点之间的分层情况。
特别地，x[1]=1

pos[i]>pos[i+1]

显然dep[i+1]≤dep[i]，但是i+1比i在深度优先遍历中先遍历到，只能说明i+1和i不是同一层的。x[i]=1

d[i]<d[i+1]

那么x[d[i]]+x[d[i]+1]+⋯+x[d[i+1]−1]<=1，也就是d[i]和d[i+1]之间最多分一层，对应了dfs序的性质，dep[d[i+1]]−dep[d[i]]<=1，如果x[d[i]],x[d[i]+1]⋯x[d[i+1]−1]直接有任何一个地方因为上一个条件分层了，那么这里就不能分了。
否则这一段内可以分一层，可以不分层，概率相等，所以我们令x[d[i]]=0.5，代表这一段的分层情况。

最后求答案就很简单了

ans=∑i=1n−1x[i]

代码

#include<cstdio>
#include<algorithm>
using namespace std;
#define MAXN 200000
int a[MAXN+10],b[MAXN+10],d[MAXN+10],pos[MAXN+10],g[MAXN+10],sta[MAXN+10],tp,n;
double x[MAXN+10],s[MAXN+10],ans=1;
void Read(int &x){
    char c;
    while(c=getchar(),c!=EOF)
        if(c>='0'&&c<='9'){
            x=c-'0';
            while(c=getchar(),c>='0'&&c<='9')
                x=x*10+c-'0';
            ungetc(c,stdin);
            return;
        }
}
void read(){
    Read(n);
    int i;
    for(i=1;i<=n;i++){
        Read(d[i]);
        a[d[i]]=i;
    }
    for(i=1;i<=n;i++){
        Read(b[i]);
        pos[i]=a[b[i]];
        d[pos[i]]=i;
    }
}
void solve(){
    int i;
    x[1]=1;
    for(i=1;i<n;i++){
        if(pos[i]>pos[i+1])
            x[i]=1.0;
        if(x[i]==1.0)
            g[i]++,g[i+1]--;
        s[i]=s[i-1]+x[i];
    }
    for(i=1;i<n;i++){
        if(d[i]<d[i+1]){
            if(s[d[i+1]-1]-s[d[i]-1]>1e-8)
                g[d[i]]++,g[d[i+1]]--;
            else
                sta[++tp]=d[i];
        }
    }
    for(i=1;i<=n;i++)
        g[i]+=g[i-1];
    for(i=1;i<=tp;i++)
        if(!g[sta[i]])
            x[sta[i]]=0.5;
    for(i=1;i<=n;i++)
        ans+=x[i];
}
int main()
{
    read();
    solve();
    printf("%.3lf\n",ans);
}