【DP】[NOI2013]书法家

题目描述

小 E 同学非常喜欢书法，他听说 NOI2013 已经开始了，想题一幅 “NOI” 的字送给大家。

小 E 有一张非常神奇的纸，纸可以用一个 n 行 m 列的二维方格矩阵来表示，为了描述方便，我们定义矩阵左下角方格坐标为 (1,1)，右上角方格坐标为 (m,n)。

矩阵的每个方格有一个整数的幸运值。在格子上面写字可以增加大家的幸运度，幸运度的大小恰好是所有被笔写到的方格的幸运值之和。现在你要在上面写上 “N”, “O”, “I” 三个字母。

下面给出 3 个书法字的定义:

  1. “N” 由若干 （≥3） 个边平行于坐标轴的矩形组成，设由 K 个矩形组成（标号 1∼K），第 i 个矩形的左下角方格坐标设为 (Li,Bi)，右上角坐标设为 (Ri,Ti)，要求满足：
    • Li≤Ri,Bi≤Ti
    • 对任意 1<i≤K，有 Li=Ri−1+1
    • 对任意 3≤i<K，有 Bi−1−1≤Ti≤Ti−1，Bi≤Bi−1
    • B2>B1，T2=T1，BK−1=BK，TK−1<TK
  2. “O” 由一个大矩形 A，挖去一个小矩形 B 得到，这两个矩形的边都平行于坐标轴。设大矩形 A 左下角的方格坐标为 (u,v)，长为 W，宽为 H，则小矩形 B 满足左下角方格坐标为 (u+1,v+1)，长 W−2，宽 H−2。要求满足：
    • W≥3,H≥3
    • u>RK+1
  3. “I” 为 3 个边平行于坐标轴的从下到上的实心矩形组成，从下到上依次标号为 1,2,3，第 i 个矩形的左下角格子坐标设为 (Pi,Qi)，右上角格子坐标设为 (Gi,Hi)，要求满足：
    • Pi≤Gi,Qi≤Hi
    • P1=P3>u+W，G1=G3
    • Q1=H1=Q2−1，H2+1=Q3=H3
    • P1<P2≤G2<G1

下图是一个 “N”，“O”，“I” 的例子。

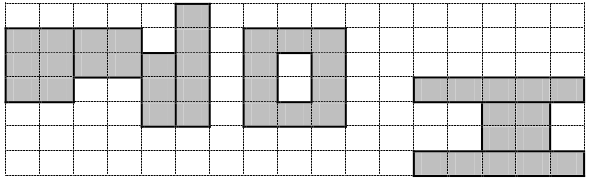
NOI的例子

另外，所有画的图形均不允许超过纸张的边界。现在小 E 想要知道，他能画出的最大幸运度是多少。

输入格式

第一行包含两个正整数 n 和 m，分别表示矩阵的行数和列数。

接下来 n 行，每行有 m 个整数，第 i+1 行的第 j 个数表示格子 (j, n − i + 1)(j,n−i+1) 的幸运值。

输出格式

输出一个整数 T，表示小 E 能够获得的最大幸运度。

样例一

input

3 13
1 1 -1 -1 1 -1 1 1 1 -1 1 1 1
1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1
1 -1 -1 1 1 -1 1 1 1 -1 1 1 1

output

24

样例二

input

3 13
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

output

-20

样例三

见样例数据下载。

限制与约定

测试点编号 n m 幸运值范围
1=3=12[−50,50]
2
3
4
5≤10≤20[−50,50]
6
7
8
9≤150≤500=1
10
11≤80≤80[−200,200]
12
13
14
15≤150≤500[−200,200]
16
17
18
19
20

对于所有的测试数据，保证 n≥3,m≥12。

时间限制：2s

空间限制：512MB

分析

很自然地分成9个部分进行动态规划，即把NOI3个字母，每个字母分别从左到右分为3部分，然后逐列进行转移。
除了N的第二部分其余的都很好转移，具体怎么转移的呢？其实也就是按照他的规则进行模拟，看代码就能理解了。

代码

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define MAXN 150
#define MAXM 500
#define INF 0x3fffffff
int a[MAXN+10][MAXM+10],n,m,blk[MAXM+10][2],f[2][10][MAXN+10][MAXN+10],s[MAXN+10][MAXM+10],tmp[MAXN+10][MAXN+10],ans=-INF;
void Read(int &x){
    static char c;
    bool f(0);
    while(c=getchar(),c!=EOF){
        if(c=='-')
            f=1;
        else if(c>='0'&&c<='9'){
            x=c-'0';
            while(c=getchar(),c>='0'&&c<='9')
                x=x*10+c-'0';
            ungetc(c,stdin);
            if(f)
                x=-x;
            return;
        }
    }
}
void read(){
    Read(n),Read(m);
    int i,j;
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++){
            Read(a[i][j]);
            s[i][j]=s[i-1][j]+a[i][j];
        }
}
void dp(){
    int i,j,k;
    memset(f[1],0xb0,sizeof f[1]);
    for(i=1;i<=n;i++)
        for(j=i;j<=n;j++)
            f[1][1][i][j]=s[j][1]-s[i-1][1];
    blk[1][0]=blk[1][1]=-INF;
    for(k=2;k<=m;k++){
        memset(f[k&1],0xb0,sizeof f[k&1]);
        //N的第一部分
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++)
                f[k&1][1][i][j]=max(s[j][k]-s[i-1][k],f[(k&1)^1][1][i][j]+s[j][k]-s[i-1][k]);
        //N的第二部分
        for(i=1;i<=n;i++){
            tmp[i][n+1]=-INF;
            for(j=n;j>=i;j--)
                tmp[i][j]=max(tmp[i][j+1],f[(k&1)^1][1][i][j]);
            }
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++){
                f[k&1][2][i][j]=max(f[k&1][2][i][j],tmp[i][j+1]+s[j][k]-s[i-1][k]);
                tmp[i][j]=-INF;
            }
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++)
                tmp[j+1][j+1]=max(tmp[j+1][j+1],f[(k&1)^1][2][i][j]);
        for(i=1;i<=n;i++)
            for(j=i+1;j<=n;j++)
                tmp[i][j]=max(tmp[i][j],tmp[i][j-1]);
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++)
                f[k&1][2][i][j]=max(f[k&1][2][i][j],tmp[i][j]+s[j][k]-s[i-1][k]);
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++)
                tmp[i][j]=f[(k&1)^1][2][i][j];
        for(j=1;j<=n;j++)
            for(i=1;i<j;i++)
                tmp[i+1][j]=max(tmp[i+1][j],tmp[i][j]);
        for(i=1;i<=n;i++)
            for(j=i;j<n;j++)
                tmp[i][j+1]=max(tmp[i][j+1],tmp[i][j]);
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++)
                f[k&1][2][i][j]=max(f[k&1][2][i][j],tmp[i][j]+s[j][k]-s[i-1][k]);
        //N的第三部分
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++)
                tmp[i][j]=f[(k&1)^1][2][i][j];
        for(j=1;j<=n;j++)
            for(i=j;i>1;i--)
                tmp[i-1][j]=max(tmp[i-1][j],tmp[i][j]);
        for(i=1;i<=n;i++)
            for(j=i+1;j<=n;j++)
                f[k&1][3][i][j]=max(f[k&1][3][i][j],max(tmp[i+1][j],f[(k&1)^1][3][i][j])+s[j][k]-s[i-1][k]);
        //NO之间空白
        blk[k][0]=blk[k-1][0];
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++)
                blk[k][0]=max(blk[k][0],f[(k&1)^1][3][i][j]);
        //O的第一部分
        for(i=1;i<=n;i++)
            for(j=i+2;j<=n;j++)
                f[k&1][4][i][j]=blk[k-1][0]+s[j][k]-s[i-1][k];
        //O的第二部分
        for(i=1;i<=n;i++)
            for(j=i+2;j<=n;j++)
                f[k&1][5][i][j]=max(f[(k&1)^1][4][i][j],f[(k&1)^1][5][i][j])+a[i][k]+a[j][k];
        //O的第三部分
        for(i=1;i<=n;i++)
            for(j=i+2;j<=n;j++)
                f[k&1][6][i][j]=f[(k&1)^1][5][i][j]+s[j][k]-s[i-1][k];
        //OI之间空白
        blk[k][1]=blk[k-1][1];
        for(i=1;i<=n;i++)
            for(j=i;j<=n;j++)
                blk[k][1]=max(blk[k][1],f[(k&1)^1][6][i][j]);
        //I的第一部分
        for(i=1;i<=n;i++)
            for(j=i+2;j<=n;j++)
                f[k&1][7][i][j]=max(blk[k-1][1],f[(k&1)^1][7][i][j])+a[i][k]+a[j][k];
        //I的第二部分
        for(i=1;i<=n;i++)
            for(j=i+2;j<=n;j++)
                f[k&1][8][i][j]=max(f[(k&1)^1][7][i][j],f[(k&1)^1][8][i][j])+s[j][k]-s[i-1][k];
        //I的第三部分
        for(i=1;i<=n;i++)
            for(j=i+2;j<=n;j++){
                f[k&1][9][i][j]=max(f[(k&1)^1][8][i][j],f[(k&1)^1][9][i][j])+a[i][k]+a[j][k];
                ans=max(ans,f[k&1][9][i][j]);
            }   
    }
}
int main()
{
    read();
    dp();
    printf("%d\n",ans);
}
posted @ 2016-07-07 22:32  outer_form  阅读(218)  评论(0)  编辑  收藏  举报