【线段树】[NOI2016]区间

题目描述

在数轴上有 n 个闭区间 [l1,r1],[l2,r2],...,[ln,rn]。现在要从中选出 m 个区间，使得这 m 个区间共同包含至少一个位置。换句话说，就是使得存在一个 x，使得对于每一个被选中的区间 [li,ri]，都有 li≤x≤ri。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 [li,ri] 的长度定义为 ri−li，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 −1。

输入格式

第一行包含两个正整数 n,m，用空格隔开，意义如上文所述。保证 1≤m≤n。

接下来 n 行，每行表示一个区间，包含用空格隔开的两个整数 li 和 ri 为该区间的左右端点。

输出格式

只有一行，包含一个正整数，即最小花费。

样例一

input

6 3
3 5
1 2
3 4
2 2
1 5
1 4

output

2

explanation

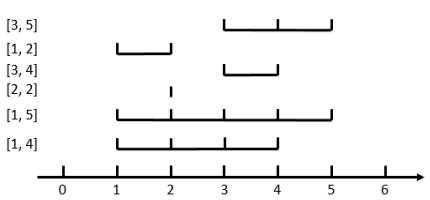
如图，当 n=6, m=3 时，花费最小的方案是选取 [3,5]、[3,4]、[1,4] 这三个区间，他们共同包含了 4 这个位置，所以是合法的。其中最长的区间是 [1,4]，最短的区间是 [3,4]，所以它的花费是 (4−1)−(4−3)=2。

样例二

见样例数据下载。

样例三

见样例数据下载。

限制与约定

所有测试数据的范围和特点如下表所示：

测试点编号	n	m	li,ri
1	20	9	0≤li≤ri≤100
2		10
3	199	3	0≤li≤ri≤100000
4	200
5	1000	2
6	2000
7	199	60	0≤li≤ri≤5000
8	200	50
9			0≤li≤ri≤109
10	1999	500	0≤li≤ri≤5000
11	2000	400
12		500	0≤li≤ri≤109
13	30000	2000	0≤li≤ri≤100000
14	40000	1000
15	50000	15000
16	100000	20000
17	200000		0 \le l_i \le r_i \le 10^90≤li≤ri≤109
18	300000	50000
19	400000	90000
20	500000	200000

时间限制：3s

空间限制：256MB

下载

样例数据下载

分析

离散化，按照区间长度排序，维护一个双指针，滑动窗口，用一个线段树来维护点被覆盖的次数即可。

代码

#include<cstdio>
#include<algorithm>
using namespace std;
#define MAXN 500000
int r[MAXN*2+10],rcnt,m,n,ans=0x7fffffff;
struct itv{
    int l,r,len;
    inline itv(){
    }
    inline itv(int l,int r):l(l),r(r),len(r-l){
    }
    bool operator<(const itv &b)const{
        return len<b.len;
    }
}a[MAXN+10];
struct node{
    int tagp,tag0,mx;
}tree[MAXN*8+10];
inline void push_down(int i){
    if(tree[i].tag0){
        tree[i<<1].tag0=tree[(i<<1)|1].tag0=1;
        tree[i<<1].mx=tree[i<<1].tagp=0;
        tree[(i<<1)|1].mx=tree[(i<<1)|1].tagp=0;
        tree[i].tag0=0;
    }
    if(tree[i].tagp){
        tree[i<<1].mx+=tree[i].tagp,tree[(i<<1)].tagp+=tree[i].tagp;
        tree[(i<<1)|1].mx+=tree[i].tagp,tree[(i<<1)|1].tagp+=tree[i].tagp;
        tree[i].tagp=0;
    }
}
inline void update(int i){
    tree[i].mx=max(tree[i<<1].mx,tree[(i<<1)|1].mx);
}
void insert(int i,int l,int r,int ll,int rr,int d){
    if(ll<=l&&r<=rr){
        tree[i].tagp+=d;
        tree[i].mx+=d;
        return;
    }
    if(ll>r||rr<l)
        return;
    int mid((l+r)>>1);
    push_down(i);
    insert(i<<1,l,mid,ll,rr,d);
    insert((i<<1)|1,mid+1,r,ll,rr,d);
    update(i);
}
int get_mx(int i,int l,int r,int ll,int rr){
    if(ll<=l&&r<=rr)
        return tree[i].mx;
    if(ll>r||rr<l)
        return 0;
    int mid((l+r)>>1);
    push_down(i);
    return max(get_mx(i<<1,l,mid,ll,rr),get_mx((i<<1)|1,mid+1,r,ll,rr));
}
void Read(int &x){
    static char c;
    bool f(0);
    while(c=getchar(),c!=EOF){
        if(c=='-')
            f=1;
        else if(c>='0'&&c<='9'){
            x=c-'0';
            while(c=getchar(),c>='0'&&c<='9')
                x=x*10+c-'0';
            ungetc(c,stdin);
            if(f)
                x=-x;
            return;
        }
    }
}
void read(){
    Read(n),Read(m);
    int i,L,R;
    for(i=1;i<=n;i++){
        Read(L),Read(R);
        r[++rcnt]=L,r[++rcnt]=R;
        a[i]=itv(L,R);
    }
    sort(r+1,r+rcnt+1);
    rcnt=unique(r+1,r+rcnt+1)-r-1;
    for(i=1;i<=n;i++){
        a[i].l=lower_bound(r+1,r+rcnt+1,a[i].l)-r;
        a[i].r=lower_bound(r+1,r+rcnt+1,a[i].r)-r;
    }
    sort(a+1,a+n+1);
}
void solve(){
    int i=1,j=2;
    tree[1].tag0=1,tree[1].tagp=tree[1].mx=0;
    insert(1,1,rcnt,a[1].l,a[1].r,1);
    while(i<=n){
        while(j<=n&&tree[1].mx<m){
            insert(1,1,rcnt,a[j].l,a[j].r,1);
            j++;
        }
        if(tree[1].mx<m)
            break;
        ans=min(ans,a[j-1].len-a[i].len);
        insert(1,1,rcnt,a[i].l,a[i].r,-1);
        i++;
    }
}
int main()
{
    read();
    solve();
    if(ans==0x7fffffff)
        puts("-1");
    else
        printf("%d\n",ans);
}