KMP算法

kmp

概览

解决字符串匹配的问题，是一种模式匹配算法，可以在 O(n+m) 的时间复杂度内实现两个字符串的匹配。

模式匹配：给定一个主串，以及一个模式串，在主串中匹配是否存在模式串并返回具体的位置

暴力法

// s 为主串，t 为模式串
int searchSubStr(char* s, int m, char* t, int n) {
    for (int i = 0; i < m - n; ++i) {
        int k = i;
        for (int j = 0; j < n; ++j) {
            if (s[k] != s[j]) break;
            ++k;
        }
        // 模式匹配完成
        if (k == n) return i;
    }
    return -1;
}

前缀表

前缀：包含首字符，不包含末尾字符的子串

后缀：不包含首字符，包含末尾字符的子串

示例：aabaaf

• 前缀：

• 后缀：

前缀表：最长相等的前后缀（都是从左向右看）

字符串	最长相等前后缀
a	0
aa	1
aab	0
aaba	1
aabaa	2
aabaaf	0

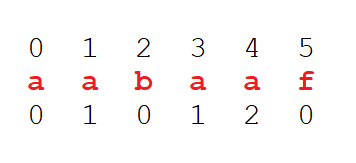
当某一位不匹配时，查看前一位的前缀表值，以该值为下标，从该处继续开始匹配

例如：用aabaaf去匹配aabaabaaf

1. 当匹配到 i=5 时出现了不相符。查看第对应 j=5 的前一个元素 j=4 的前缀值，为2。
2. 保持主串 i=5 下标不变，子串从下标 j=2 处继续向后匹配。相当于将子串向右移动了（5-2）位

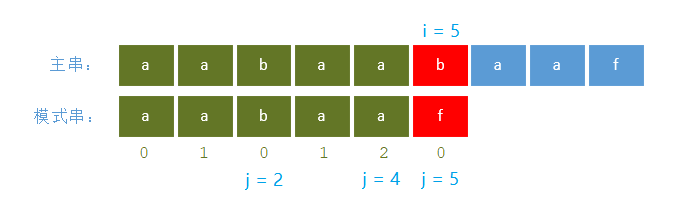
i = 5，j = 2 继续向后匹配

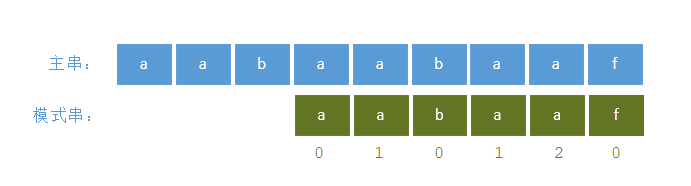
初始化next数组

vector<int>& getNext(string str)
{
    int len = str.size();
    vector<int>* next = new vector<int>();
    next->resize(len);
    for (int i = 1; i <= len; ++i) {
        string subStr = str.substr(0, i);
        for (int j = i - 1; j >= 1; --j) {
            if (subStr.substr(0, j).compare(subStr.substr(i - j, j)) == 0) {
                (*next)[i - 1] = j;
		break;
	    }
        }
    }
    return *next;
}

利用next数组查找

int findKMP(string src, string tar) {
    vector<int> next = getNext(tar);
    int len1 = src.size();
    int len2 = tar.size();
    int tar = 0;    // 主串中将要匹配的位置
    int pos = 0;    // 模式串中将要匹配的位置
    while (tar < len1) {
        if (src[tar] == tar[pos]) {    // 若相等，则各自下标右移
            ++tar;
            ++pos;
        } else if (pos != 0) {    // 若不等且pos≠0，则利用next数组，将pos退到指定位置
            pos = next[pos - 1];
        } else {
            ++tar;    // 否则将主串下标右移
        }

        if (tar > len1 - len2 && pos == 0) break;
        if (pos == len2) return tar - pos;
    }

    return -1;
}

next数组的求法

快速求next数组是KMP算法的精髓所在。核心思想是“P自己与自己做匹配”

• 定义：“k-前缀”为一个字符串的前k个字符；“k-后缀”为一个字符串的后k个字符。k必须小于字符串长度
• next[x]定义：p[0]~p[x]这一段字符串，使得k前缀等于k后缀的最大的k
  • 这个定义中不自觉地包含了一个匹配——前缀和后缀相等。
  • 可以利用已知的next[0],next[1],...next[x-1]来求next[x]。（前后缀进行匹配）

前缀串A和后缀串B已知。在求P[x]时，比较前缀串的后一个字符P[now]，

• 如相等，则P[x] = P[x-1] + 1，前缀串A和后缀串B长度各自增加一；
• 如不等，则应该将P[now]左移，缩短now，把它改小一点，然后再试试P[now]是否等于P[x]。

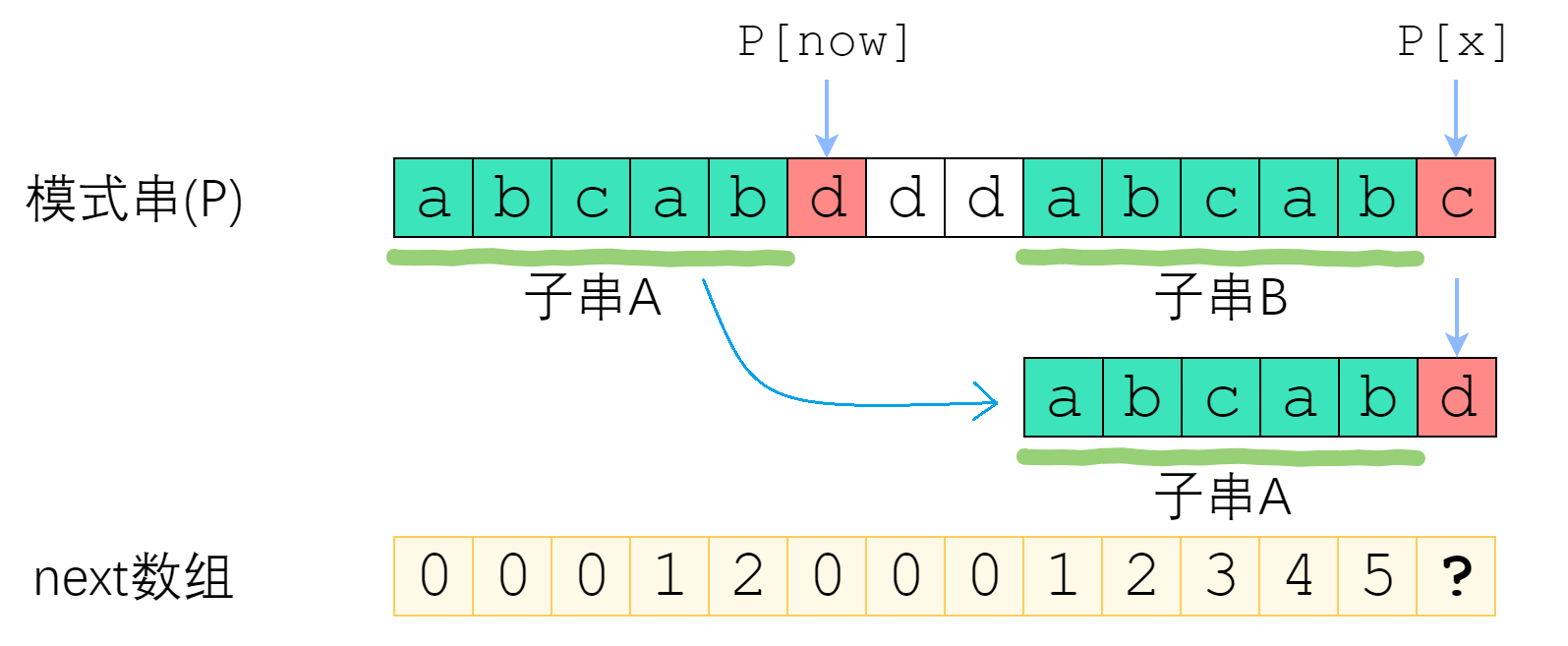
关于now应该缩小多少呢？

• 最终的目的是让前缀串A和后缀串B都尽可能的长，且前缀串A的下一个字符P[now]==P[x]
• 即寻找A和B的最长k-前后缀串，使得A的k-前缀等于B的k-后缀的最大的k
• 因为前缀串A和后缀串B相同，可得：B的后缀等于A的后缀，B的前缀等于A的前缀
• 使得A的k-前缀等于B的k-后缀的最大的k，其实就是串A的最长公共前后缀的长度 next[now-1]

• 当P[now]与P[x]不相等的时候，我们需要缩小now——把now变成next[now-1]，直到 P[now]==P[x] 为止。
• P[now]==P[x] 时，就可以直接向右扩展了，next[x] = now + 1。

vector<int> getNex(string str) {
    vector<int> nex;
    nex.push_back(0);

    int x = 1;    // next[0]必然是0，因此从next[1]开始求
    int now = 0;
    int len = str.size();

    while (x < len) {
        if (str[now] == str[x]) {    // 如果p[now] == p[x]，则都向右移动
            now++;
            x++;
            nex.push_back(now);
        } else if (now) {
            now = nex[now - 1];	// 利用next[]数组缩小now，类似与kmp，自己和自己匹配
        } else {
            nex.push_back(0);	// now已经为0，无法再缩，故next[x] = 0
            x++;
        }
    }
    return nex;
}

现在我着重讲解一下while循环所做的工作：

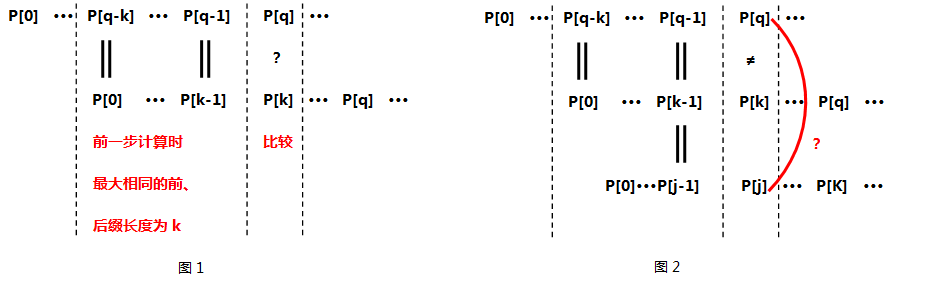
1. 已知前一步计算时最大相同的前后缀长度为k（k>0），即P[0]···P[k-1]；
2. 此时比较第k项P[k]与P[q],如图1所示
3. 如果P[K]等于P[q]，那么很简单跳出while循环;
4. 关键！关键如果不等呢？？？那么我们应该利用已经得到的next[0]···next[k-1]来求P[0]···P[k-1]这个子串中最大相同前后缀，可能有同学要问了——为什么要求P[0]···P[k-1]的最大相同前后缀呢？？？
5. 原因在于P[k]已经和P[q]失配了，而且P[q-k] ··· P[q-1]又与P[0] ···P[k-1]相同，看来P[0]···P[k-1]这么长的子串是用不了了，那么我要找个同样也是P[0]打头、P[k-1]结尾的子串即P[0]···P[j-1](j==next[k-1])，看看它的下一项P[j]是否能和P[q]匹配。如图2所示

简化

void getNex(const char *s)
{
    /*更新模式串s的nex数组*/
    int len = strlen(s);
    vector<int> nex(len);
    
    //for循环，从第二个字符开始，依次计算每一个字符对应的next值
    for (int x = 1, now = 0; x < len; ++x) {
        //递归的求出P[0]···P[q]的最大的相同的前后缀长度k
        while (now > 0 && s[now] != s[x]) now = nex[now - 1];
        if (s[now] == s[x]) ++now;    //如果相等，那么最大相同前后缀长度加1
        nex[x] = now;
    }
}

严蔚敏版

void getNex2(const char *s)
{
    /*更新模式串s的nex数组*/
    int len = strlen(s);
    vector<int> nex(len);
    for (int i = 2, j = 0; i < len; ++i) {
        while (j > 0 && s[i - 1] != s[j]) j = nex[j];
        j++;
        nex[i] = j;
    }
}

code

int search(string str, string goal) {
    vector<int> nex(goal.size());
    for (int now = 0, x = 1; x < goal.size(); ++x) {
        while (now > 0 && goal[now] != goal[x]) now = nex[now - 1];
        if (goal[now] == goal[x]) ++now;
        nex[x] = now;
    }

    for (int now = 0, x = 1; x < str.size(); ++x) {
        while (now > 0 && goal[now] != str[x]) now = nex[now - 1];
        if (goal[now] == str[x]) ++now;
        if (now == goal.size()) return x - now + 1;
    }
    return -1;
}

参考：
https://www.ruanx.net/kmp/
https://www.cnblogs.com/c-cloud/p/3224788.html