快速排序
概述：
快速排序是从冒泡排序演变而来，但比冒泡排序高效的多，所以叫做快速排序。同冒泡排序一样，快速排序也属于交换排序，通过元素之间的比较和交换位置来达到排序的目的。不同的是它采用了分治法。
冒泡排序在每一轮只把一个元素冒泡到数列的一端，而快速排序在每一轮挑选一个基准元素，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成了两个部分。
示例：
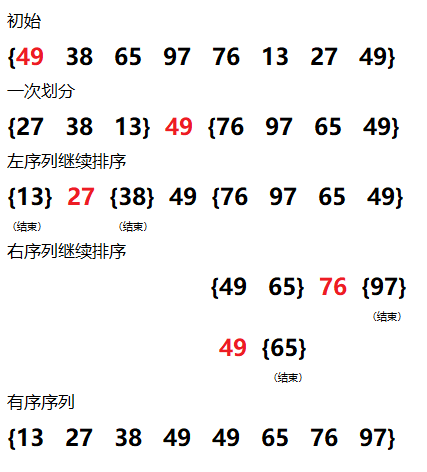
具体实现
挖坑法
1 public static <T extends Comparable<? super T>> void quickSort(T[] arr, int start, int end) { 2 if (start >= end) return; 3 4 int i = start; 5 int j = end; 6 T key = arr[start]; 7 while (i < j) { 8 /*按j--方向遍历目标数组，直到比key小的值为止*/ 9 while (i < j && arr[j].compareTo(key) >= 0) j--; 10 if (i < j) arr[i++] = arr[j]; 11 12 /*按i++方向遍历目标数组，直到比key大的值为止*/ 13 /*此处一定要小于等于零，假设数组之内有一亿个1,0交替出现的话，而key的值又恰巧是1的话， 14 那么这个小于等于的作用就会使下面的 if 语句少执行一亿次。*/ 15 while (i < j && arr[i].compareTo(key) <= 0) i++; 16 if (i < j) arr[j--] = arr[i]; 17 } 18 /*此时i==j*/ 19 arr[i] = key; 20 21 quickSort(arr, start, i - 1); 22 quickSort(arr, j + 1, end); 23 }
指针交换法
1 public static void quickSort(int[] arr, int start, int end) { 2 if (start >= end) return; 3 4 int pivot = arr[start]; 5 int i = start; 6 int j = end; 7 while (i < j) { 8 while ((arr[j] >= pivot) && (i < j)) j--; 9 while ((arr[i] < pivot) && (i < j)) i++; 10 11 if (i < j) { 12 arr[i] = arr[i] ^ arr[j]; 13 arr[j] = arr[i] ^ arr[j]; 14 arr[i] = arr[i] ^ arr[j]; 15 } 16 } 17 arr[start] = arr[i]; 18 arr[i] = pivot; 19 20 quickSort(arr, start, i - 1); 21 quickSort(arr, j + 1, end); 22 }
性能分析：
时间复杂度：
快速排序的一次划分算法从两头交替搜索，直到 low 和 high 重合，因此其时间复杂度是 O(n)；而整个快速排序算法的时间复杂度与划分的趟数有关。
理想的情况是，每次划分所选择的中间数恰好将当前序列几乎等分，经过 log2n 趟划分，便可得到长度为1的子表。这样，整个算法的时间复杂度为 O(nlog2n)。
最坏的情况是，每次所选的中间数是当前序列中的最大或最小元素，这使得每次划分所得的子表中一个为空表，另一子表的长度为原表的长度-1。这样，长度为n的数据表的快速排序需要经过n趟划分，使得整个排序算法的时间复杂度为 O(n2)。
为改善最坏情况下的时间性能，可采用其他方法选取中间数。通常采用“三者值取中”方法，
即比较 H->r[low].key、H->r[high].key 与 H->r[(10w+high)/2].key，取三者中关键字为中值的元素为中间数。
可以证明，快速排序的平均时间复杂度也是 O(nlog2n)。因此，该排序方法被认为是目前最好的一种内部排序方法。
空间复杂度：
从空间性能上看，尽管快速排序只需要一个元素的辅助空间，但快速排序需要一个栈空间来实现递归。最好的情况下，即快速排序的每一趟排序都将元素序列均匀地分割成长度相近的两个子表，所需栈的最大深度为 log2(n+1)；但最坏的情况下，栈的最大深度为 n。这样，快速排序的空间复杂度为 O(log2n))。
