建模股票价格数据并进行预测(统计信号模型):随机信号AR模型+Yule-Walker方程_Python
1.背景:
针对股票市场中AR 模型的识别、建立和估计问题,利用AR 模型算法对股票价格进行预测。
2.模型选取:
股票的价格可视为随机信号,将此随机信号建模为:一个白噪声通过LTI系统的输出,通过原始数据求解 所建模型参数,得到模型,即可预测近期未来的未知股票价格。
随机信号建模为:白噪声通过滤波器,滤波器的系统函数为:
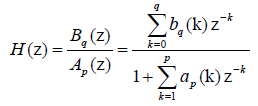
其中,bq,ap为滤波器系数,根据参数的不同,此滤波器的类型相应有三种。
(1)AR模型(Auto-Regreesion)
此时,滤波器系数为bq(分子)为1,系统主要依赖于过去输出的反馈作用(分母),这是一种特殊的IIR滤波器。
AR模型中,序列X当前值由序列e的当前值和序列X的前一个长度为M的窗口内序列值决定。
原理:自回归模型(Autoregressive Model,AR Model)是用自身做回归变量的过程,即利用前期若干时刻的随机变量的线性组合来描述以后某时刻随机变量的线性回归模型。
(2)MA模型(画的平均)
此时,滤波器系数ap(分母)为1,无反馈,系统主要依赖于白噪声样本加权求和输出,FIR滤波器。
(3)ARMA模型
bq,ap都不为1,是一种典型的IIR滤波器。
这三种模型中,AR模型的特别之处是它具有预测特性,把所有能用过去值预测的都表达了,只剩下输入导致的变化。故我们的预测模型使用AR模型。
AR 是对平稳时间序列成立的,平稳大致上意味着该序列没有趋势,围绕着一个均值上下波动。为了将股票价格平稳化,先对股价进行差分处理。然后使用Yule—Walker 方程求解模型系数,模型的阶数通过试探的方法确定。预测时程序可选择使用模型预测天数,本程序使用六阶模型预测未来近三日的股价。
步骤:
考虑一组随机自变量观测值与因变量观测值之间的关系,设自变量观测值为x(n),因变量观测值为Y=[y(n),y(n-1),…,y(n-N)],则依据AR Model,满足如下关系式:
\[{a_0}y\left( n \right) + {a_1}y\left( {n - 1} \right) + \cdot \cdot \cdot + {a_N}y\left( {n - N} \right) = x\left( n \right)\]
其中,a=[a0,a1,…aN]为各项因变量观测值系数。通常情况下,我们令a0=1。考虑到上式的迭代性,我们可以将其转化为一组自变量观测值和一个因变量观测值的形式如下:
\[y\left( n \right) = x\left( n \right) + {\alpha _1}x\left( {n - 1} \right) + {\alpha _2}x\left( {n - 2} \right) + \cdot \cdot \cdot \]
其中,A=[]是各项自变量观测值的系数。另外,我们假定自变量观测值的自相关函数为:
\[{\rm{E}}\left\{ {\left. {x\left( n \right)x\left( {n - k} \right)} \right\}} \right. = {\sigma ^2}\delta \left( k \right)\]
其中:\[{\sigma ^2}\]是自变量观测值的方差; \[\delta \left( k \right)\]是狄拉克函数。
将所得的y(n)代入可得:
\[{\rm{E}}\left\{ {\left. {y\left( n \right)x\left( n \right)} \right\}} \right. = {\rm{E}}\left\{ {\left. {\left[ {x\left( n \right) + {\alpha _1}x\left( {n - 1} \right) + \cdot \cdot \cdot } \right]x\left( n \right)} \right\}} \right. = {\sigma ^2}\]
同样,将任意的一个y(n-K)代入可得:
\[{\rm{E}}\left\{ {\left. {y\left( {n - k} \right)x\left( n \right)} \right\}} \right. = {\sigma ^2}\delta \left( k \right)\]

将因变量观测值(Y(n)的自相关)的自相关函数写成矩阵形式可得如下:
\[\left[ {\begin{array}{*{20}{c}}
{{r_0}}&{{r_1}}& \cdots &{{r_{N - 1}}}\\
{{r_1}}&{{r_0}}& \cdots &{{r_{N - 2}}}\\
\vdots & \vdots & \vdots & \vdots \\
{{r_{N - 1}}}&{{r_{N - 2}}}& \cdots &{{r_0}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{a_1}}\\
{{a_2}}\\
\vdots \\
{{a_N}}
\end{array}} \right] = - \left[ {\begin{array}{*{20}{c}}
{{r_1}}\\
{{r_2}}\\
\vdots \\
{{r_N}}
\end{array}} \right]\]
该矩阵由Yule-Walker方程描述为:\[Ra = - r\]
对于该系统预测的关键在于对系统系数向量a的求解。将AR Model方程写成如下形式:
\[y\left( n \right) = - \sum\limits_{k = 1}^N {{a_k}y\left( {n - k} \right)} + x\left( n \right)\]
将因变量观测值y(n)的L个观测值写成矩阵形式如下:
\[\left[ {\begin{array}{*{20}{c}}
{y\left( N \right)}\\
{y\left( {N + 1} \right)}\\
\vdots \\
{y\left( {L - 1} \right)}
\end{array}} \right] = - \left[ {\begin{array}{*{20}{c}}
{y\left( {N - 1} \right)}&{y\left( {N - 2} \right)}& \cdots &{y\left( 0 \right)}\\
{y\left( N \right)}&{y\left( {N - 1} \right)}& \cdots &{y\left( 1 \right)}\\
\vdots & \vdots & \vdots & \vdots \\
{y\left( {L - 2} \right)}& \cdots & \cdots &{y\left( {L - N - 1} \right)}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{a_1}}\\
{{a_2}}\\
\vdots \\
{{a_N}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{x\left( N \right)}\\
{x\left( {N + 1} \right)}\\
\vdots \\
{x\left( {L - 1} \right)}
\end{array}} \right]\]
将上式写成Yule-Walker方程形式为:\[y = - Ya + x\]。其中,x是自变量观测值矩阵,a是系数矩阵,Y是Toeplitz矩阵,y是因变量观测值矩阵。
使用最小二乘法(Least Square,LS)寻找一个最优解为:\[{\left\| x \right\|^2} = {\left( {y + Ya} \right)^H}\left( {y + Ya} \right)\]。对该式进行求解可得:\[a = - {\left( {{Y^H}Y} \right)^{ - 1}}{Y^H}y\]。将所求系数代入即可得到拟合方程,根据拟合方程可以得到问题的估计值。
AR模型结束确定(Matlab):
研究表明,采用Yule-Walker方法可得到优化的AR模型,故采用aryule程序估计模型参数。
[m,refl] = ar(y,n,approach,window)
yp = predict(m,y,k)
表示预测模型;为实际输出;预测区间;yp为预测输出。
当k<Inf时,yp(t)为模型m与y(1,2,…t-k)的预测值;当k=Inf时,yp(t)为模型m的纯仿真值;默认情况下,k=1。
在计算AR模型预测时,k应取1,原因参照AR模型理论公式。
compare(y,m,k)
[yh,fit,x0] = compare(y,m,k)
Compare的预测原理与predict相同,但其对预测进行了比较。
e = pe(m,data)
pe误差计算。采用yh=predict(m,data,1)进行预测,然后计算误差e=data-yh;
[e,r]= resid(m,data,mode,lags);
resid(r)
resid计算并检验误差。采用pe计算误差;在无输出的情况下,绘出误差图,误差曲线应足够小,黄色区域为99%的置信区间,误差曲线在该区域内表明通过检验。




