Python 基础语法学习
for i \
in range(3):
print(i)
print("-"*10)
0
----------
1
----------
2
----------
a = 10
b = 10.1
c = "hello"
print(a, "\n", b, "\n", c)
10
10.1
hello
print("%.3f" % 3.2)
3.200
a = "hello,world"
a0 = a[:-2]
a1 = a[1:]
print(a0, "\n", a1)
hello,wor
ello,world
list1 = [12.1, 100, "hello"]
print(list1)
list1[2] = -10
list2 = list1
print(list2)
[12.1, 100, 'hello']
[12.1, 100, -10]
# Filename : test.py
# author by : www.runoob.com
# 引入 datetime 模块
import datetime
def getYesterday():
today = datetime.date.today()
oneday = datetime.timedelta(days=1)
yesterday = today-oneday
return yesterday
# 输出
print(getYesterday())
2020-04-08
a = 10
b = 10
print("a id", id(a))
print("b id", id(b))
print("a and b", a is b)
c = 400
d = 400
print("c id", id(c))
print("d id", id(d))
print("c and d", c is d)
a id 94470720303456
b id 94470720303456
a and b True
c id 139988167345392
d id 139988167345936
c and d False
a = 1
if a == 1:
print("wow")
elif a == 2:
print("wooow")
else:
print("not")
wow
list1 = [1, 2, 3, 4]
a = 1
b = 7
print(a in list1, b in list1)
True False
def function1(string="hao are you"):
print("you say:", string)
return None
function1()
you say: hao are you
list1 = [1, 3, 4, 6, 7]
for i in list1:
print(i)
1
3
4
6
7
class number1:
number1_name = 0
number1_num1 = 0
def __init__(self, name, num1):
self.number1_name = name
self.number1_num1 = num1
def printinfo(self):
print("name:", self.number1_name, "number:", self.number1_num1)
a = number1("Jan", 101)
b = number1("May", 102)
a.printinfo()
b.printinfo()
name: Jan number: 101
name: May number: 102
a = input()
print(a)
da
da
Numpy库学习
import numpy as np
np.array([[1, 2, 3], [4, 5, 6], [1, 2, 4]])
array([[1, 2, 3],
[4, 5, 6],
[1, 2, 4]])
import numpy as np
np.ones([2, 4])
array([[1., 1., 1., 1.],
[1., 1., 1., 1.]])
import numpy as np
a = np.ones([1, 2])
a[0, 1] = -1
print(a)
[[ 1. -1.]]
import numpy as np
a = np.array(((1, 2, 3), (2, 3, 4)))
print(a)
a[0, 1] = -1
print(a)
[[1 2 3]
[2 3 4]]
[[ 1 -1 3]
[ 2 3 4]]
import numpy as np
a = np.zeros([3, 3])
print(a)
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
import numpy as np
a = np.empty([3, 5])
print(a)
[[ 6.91252072e-310 1.04179639e+038 0.00000000e+000 0.00000000e+000
-3.45901879e-144]
[ 0.00000000e+000 0.00000000e+000 1.20056986e+075 0.00000000e+000
0.00000000e+000]
[ 2.98193437e-035 0.00000000e+000 0.00000000e+000 -4.60251970e-178
0.00000000e+000]]
import numpy as np
a = np.array([[1, 2, 3], [7, 1, 5], [8, 2, 7], [5, 1, 5]])
c = a.shape
a = a.ndim
b = np.zeros([2, 4, 2, 2])
d = b.size
b = b.ndim
print(a, c, b, d)
2 (4, 3) 4 32
ndim是维数 shape是行列数 size是数组中的个数
import numpy as np
a = np.matrix([[1, 2], [7, 1]])
print(a, a.ndim, a.shape, a.size)
[[1 2]
[7 1]] 2 (2, 2) 4
matrix是矩阵
import numpy as np
a = np.matrix([[1, 2], [7, 1]])
print(a.dtype)
b = np.array([[12, 7, 5], [9, 1, 2]], dtype=np.float64)
print(b.dtype)
int64
float64
dtype是显示当前数组/矩阵的数据类型 dtype=np.int16/int32/float64是改数组数据类型
import numpy as np
a = np.matrix([[1, 2], [7, 1]], dtype=np.float64)
print(a.itemsize)
8
itemsize是给当前数组的每个数据的大小
import numpy as np
a = np.arange(1, 4001, 2, dtype=np.int16)
print(a)
[ 1 3 5 ... 3995 3997 3999]
numpy.arange()
- 概述
Numpy 中 arange() 主要是用于生成数组,具体用法如下; - arange()
2.1 语法
numpy.arange(start, stop, step, dtype = None)
在给定间隔内返回均匀间隔的值。
值在半开区间 [开始,停止]内生成(换句话说,包括开始但不包括停止的区间),返回的是 ndarray 。
2.2 参数:
start —— 开始位置,数字,可选项,默认起始值为0
stop —— 停止位置,数字
step —— 步长,数字,可选项, 默认步长为1,如果指定了step,则还必须给出start。
dtype —— 输出数组的类型。 如果未给出dtype,则从其他输入参数推断数据类型。
import numpy as np
a = np.matrix([[1, 2, 3]])
b = np.matrix([[7], [2], [4]])
c = np.array([[1, 2, 3]])
d = np.array([[7], [2], [4]])
e = np.dot(a, b)
f = a.dot(b)
print(a*b, '\n', c*d, '\n', e, '\n', f)
[[23]]
[[ 7 14 21]
[ 2 4 6]
[ 4 8 12]]
[[23]]
[[23]]
np.dot()或者a.dot()是求数组点积,及把数组相乘转为为矩阵相乘
import numpy as np
a = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
b = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(a.min(0), '\n', a.max(axis=1), '\n', b.min(), '\n', b.max())
[[1 2 3]]
[[3]
[6]
[9]]
1
9
numpy中的max() min()函数中有一个 axis形参为 0 则输出每一列的最值,为 1 则输出每行最值,不填则输出整个列表或矩阵的最值
import numpy as np
a = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(a.sum(0), '\n', a.sum(1), '\n', a.sum())
[[12 15 18]]
[[ 6]
[15]
[24]]
45
numpy中 sum()函数是求和
import numpy as np
a = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(np.exp(a), '\n', np.square(a), '\n', np.sqrt(a))
[[2.71828183e+00 7.38905610e+00 2.00855369e+01]
[5.45981500e+01 1.48413159e+02 4.03428793e+02]
[1.09663316e+03 2.98095799e+03 8.10308393e+03]]
[[ 1 4 9]
[16 25 36]
[49 64 81]]
[[1. 1.41421356 1.73205081]
[2. 2.23606798 2.44948974]
[2.64575131 2.82842712 3. ]]
np.exp()为指数运算,np.sqrt()为平方根运算,np.suare()为平方运算
***这几个函数 全在numpy类中不在定义对象中
import numpy as np
np.random.seed(11)
print(np.random.rand(2, 2))
print(np.random.rand(2, 2))
print(np.random.randn(2, 2))
c = np.random.randint(1, 10, (3, 3), np.int16)
print(c, c.dtype)
print(np.random.binomial(10, 0.6, (3, 3)))
print(np.random.beta(2, 3, (3, 3)))
print(np.random.normal(5, 1, (3, 3)))
[[0.18026969 0.01947524]
[0.46321853 0.72493393]]
[[0.4202036 0.4854271 ]
[0.01278081 0.48737161]]
[[-0.53662936 0.31540267]
[ 0.42105072 -1.06560298]]
[[9 2 7]
[4 3 7]
[4 3 2]] int16
[[8 5 5]
[7 7 8]
[8 5 6]]
[[0.48914705 0.31453808 0.61569653]
[0.42094996 0.39159773 0.06277155]
[0.34021367 0.72969676 0.20578207]]
[[6.08771086 5.53382172 5.39521201]
[5.12286753 6.20910164 4.1569339 ]
[4.85810642 5.38535414 3.42250569]]
numpy.random.seed(int x) 用于指定随机数生成时所用算法开始的整数值,如果使用相同的seed( )值,则每次生成的随即数都相同,如果不设置这个值,则系统根据时间来自己选择这个值,此时每次生成的随机数因时间差异而不同。有利于结果复现。
numpy.random.rand(d0,d1,…dn) 几行几列几维
以给定的形状创建一个数组,并在数组中加入在[0,1]之间满足均匀分布的随机样本。
numpy.random.randn(d0,d1,…dn)
以给定的形状创建一个数组,数组元素来符合标准正态分布 N(0,1) <--平均值为0方差为1
numpy.random.randint(low,high=None,size=None,dtype)
生成值为整数类型的随机样本数 ,size为几行几列
生成在半开半闭区间[low,high)上离散均匀分布的整数值;若high=None,则取值区间变为[0,low)
numpy.random.binomial(n,p,size=None)
生成一个维数指定且满足二项分布的随机样本
(下方仅供参考)
参数n:一次试验的样本数n,并且相互不干扰
参数p:事件发生的概率p,范围[0,1]
参数size:限定了返回值的形式和实验次数。当size是整数N时,表示实验N次,返回每次实验中事件发生的次数;size是(X,Y)时,表示实验X*Y次,以X行Y列的形式输出每次试验中事件发生的次数。
numpy.random.beta(a, b, size=None)
生成一个指定维度且满足beta分布的随机样本数
The Beta distribution is a special case of the Dirichlet distribution, and is related to the Gamma distribution. It has the probability distribution function
beta分布就是概率出现的概率
numpy.random.normal(loc=0.0, scale=1.0, size=None)
生成一个指定维度且满足高斯正态分布的随机样本数
loc 分布的中值("centre")
scale 分布的标准差(spread or "width")
size 输出的维数(shape)
import numpy as np
a = np.arange(1, 10, 1, np.int16)
print(a)
print(a[0:5])
for i in a:
print(i)
[1 2 3 4 5 6 7 8 9]
[1 2 3 4 5]
1
2
3
4
5
6
7
8
9
一维数组索引、切片、迭代如上
import numpy as np
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(a)
print("-"*10)
for i in a:
for j in i:
print(j)
print("-"*10)
for i in a.flat:
print(i)
[[1 2 3]
[4 5 6]
[7 8 9]]
----------
1
2
3
4
5
6
7
8
9
----------
1
2
3
4
5
6
7
8
9
通过二层嵌套循环可以完成遍历数组,也可用 .flat对数组扁平化处理,一层循环遍历数组
Matplotlib库学习
import matplotlib.pyplot as plt
%matplotlib inline
matplotlib库为python绘图库,如要直接显示绘制图像要加 %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
np.random.seed(19)
a = np.random.normal(4, 5, 30)
b = np.random.randn(30)
c = np.random.binomial(10, 0.5, 30)
plt.title("Test")
plt.xlabel("X")
plt.ylabel("Y")
x, = plt.plot(a, "r-o")
y, = plt.plot(b, "b--x")
z, = plt.plot(c, "g-.*")
plt.legend([x, y, z], ["normal", "randn", "binomial"])
print(a)
print(b)
print(c)
[ 5.10501631 2.29767496 1.11125729 1.97984222 0.98355287 2.78073861
9.17671869 6.90376706 5.26206868 -3.31272976 -3.74170661 5.32636364
3.99551896 -1.07996201 4.55994803 -1.95976026 11.7777195 -0.66649961
6.63267125 3.25017709 6.61392873 10.71077436 11.79260635 10.27997038
8.54301652 -0.2045069 9.02792549 -1.1190209 4.90886956 1.91659527]
[ 1.97840875 1.91744468 -1.031007 -0.48331191 -0.64508015 0.06034816
0.54793044 0.84514847 -1.20718132 0.37484034 0.94234783 -0.35126393
0.45973503 -0.04851666 0.41548191 -0.70187614 0.18546447 0.46834978
0.03952335 0.71614054 -0.4816884 -0.05249119 -0.27227855 0.30798526
-1.76065359 1.15022395 -0.21773107 -1.22058738 -0.34361544 1.54876219]
[3 4 9 4 7 3 8 5 6 6 5 7 2 5 4 4 6 4 6 8 5 3 3 4 4 5 7 3 6 6]
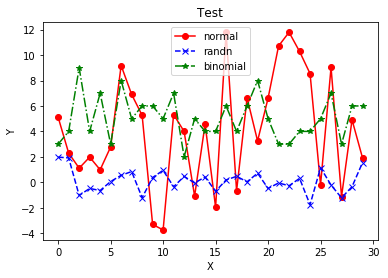
matplotlib.plot(x,y,format_string,**kwargs)
说明:
x:x轴数据,列表或数组,可选
y:y轴数据,列表或数组
format_string:控制曲线的格式字符串,可选
**kwargs:第二组或更多,(x,y,format_string)
设置线性图的颜色常用参数:
b蓝色 g绿色 r红色 m洋红色 c蓝绿色 y黄色 k黑色 w白色 ‘#008000’RGB某颜色
参数点形状:
o圆型 *星型 + x
点线条形状:
-实现 --虚线 -.点实现 :点线
plt.title("Test")为给标题
plt.xlabel("X")给x轴命名
plt.ylabel("Y")给y轴命名
plt.legend([x,y,z],["normal","randn","binomial"])给图的点做说明
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
np.random.seed(15)
a = np.random.normal(4, 5, 30)
b = np.random.randn(30)
c = np.random.binomial(10, 0.5, 30)
fig = plt.figure()
ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 2)
ax3 = fig.add_subplot(2, 2, 3)
A, = ax1.plot(a, "r-o")
ax1.legend([A], ["a"])
B, = ax2.plot(b, "b--*")
ax2.legend([B], ["b"])
C, = ax3.plot(c, "g-.+")
ax3.legend([C], ["c"])
<matplotlib.legend.Legend at 0x7f44c444aa90>
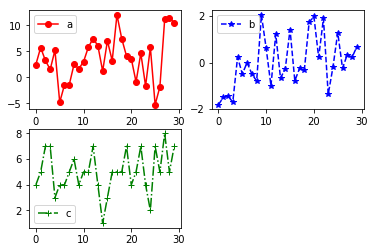
创建子图需要先调用 plt.figure() 函数,给每个图位置进行赋值用 fig.add_subplot(a,b,c) 函数
,其中 a,b 为几行几列的子图表 c为当前图在表中位置 ,最后用 plot函数将具体数据写入图中
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
np.random.seed(15)
a = np.random.randn(30)
np.random.seed(5)
b = np.random.randn(30)
plt.scatter(a,b,c="g",marker="o",label="(x,y)")
plt.legend(loc=0)
plt.title("Are you ready")
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
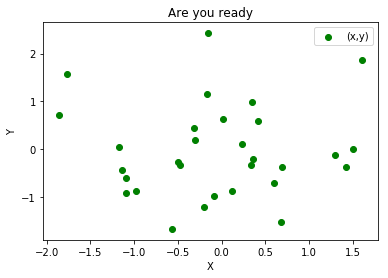
plt.scatter()函数绘制散点图,详见代码
loc=0/1/2/3/4 0为自动选 其余从第一象限逆时针
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
np.random.seed(42)
a = np.random.randn(1000)
plt.hist(a, bins=20, color="g")
plt.title("No,I'm not")
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
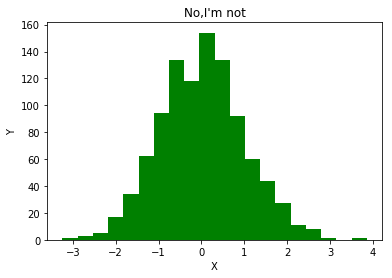
plt.hint()函数绘制直方图,bins 是条纹数
import matplotlib.pyplot as plt
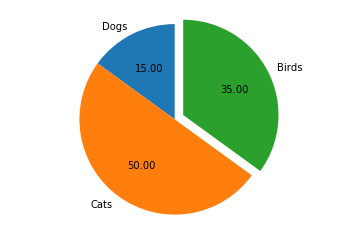
labels = ["Dogs", "Cats", "Birds"]
sizes = [15, 50, 35]
plt.pie(sizes, explode=(0, 0, 0.1), labels=labels,autopct='%1.2f', startangle=90)
plt.axis('equal')
plt.show()
PyTorch 基础学习
import torch
a = torch.FloatTensor(2, 3)
b = torch.FloatTensor([2.1, 3, 4, 5])
c = torch.IntTensor(2, 3)
d = torch.IntTensor([[1, 2, 3, 4], [2, 3, 4, 5]])
print(a)
print(b)
print(c)
print(d)
tensor([[0., 0., 0.],
[0., 0., 0.]])
tensor([2.1000, 3.0000, 4.0000, 5.0000])
tensor([[ 0, 0, 0],
[ 0, -1107135675, 1884978169]], dtype=torch.int32)
tensor([[1, 2, 3, 4],
[2, 3, 4, 5]], dtype=torch.int32)
import torch
a = torch.rand(2, 3)
b = torch.randn(2, 3)
c = torch.arange(1, 22, 2)
d = torch.zeros(2, 3)
print(a)
print(b)
print(c)
print(d)
tensor([[0.2277, 0.6782, 0.7195],
[0.7507, 0.2358, 0.0920]])
tensor([[ 0.7264, -0.5226, 0.5209],
[ 0.4460, -0.3604, 0.6802]])
tensor([ 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21])
tensor([[0., 0., 0.],
[0., 0., 0.]])
推荐使用 arange 而不是 range
arrange 第三个参数是步长
import torch
a = torch.randn(2, 3)
print(a)
b = torch.abs(a)
print(b)
print(torch.add(a, b))
print(torch.add(a, 10))
tensor([[-2.0042, 1.5977, -0.0227],
[-0.1025, -0.5865, 0.8083]])
tensor([[2.0042, 1.5977, 0.0227],
[0.1025, 0.5865, 0.8083]])
tensor([[0.0000, 3.1955, 0.0000],
[0.0000, 0.0000, 1.6166]])
tensor([[ 7.9958, 11.5977, 9.9773],
[ 9.8975, 9.4135, 10.8083]])
import torch
a = torch.IntTensor([[-2, 1, 3], [2, 7, -10]])
b = torch.clamp(a, -1, 3)
print(a)
print(b)
tensor([[ -2, 1, 3],
[ 2, 7, -10]], dtype=torch.int32)
tensor([[-1, 1, 3],
[ 2, 3, -1]], dtype=torch.int32)
torch.clamp(a,b,c) 用来对参数进行范围裁剪 第一个参数传要裁剪对象,第二个参数是下限,第三个参数是上限
import torch
a = torch.randn(2, 3)
b = torch.randn(2, 3)
print(a)
print(b)
print(torch.mul(a, b))
print(torch.mul(a, 10))
print(torch.div(a, b))
print(torch.div(10, b))
c = torch.zeros(2, 3)
print(torch.div(10, c))
print(torch.pow(a, 0))
print(torch.pow(c, 0))
tensor([[-0.5769, 1.2399, -0.8562],
[ 0.8909, 0.9248, 1.3515]])
tensor([[-0.3133, -0.2824, 0.4792],
[-0.7237, -2.1322, 2.8614]])
tensor([[ 0.1807, -0.3501, -0.4103],
[-0.6447, -1.9718, 3.8674]])
tensor([[-5.7688, 12.3990, -8.5620],
[ 8.9094, 9.2479, 13.5155]])
tensor([[ 1.8413, -4.3910, -1.7867],
[-1.2312, -0.4337, 0.4723]])
tensor([[-31.9180, -35.4140, 20.8683],
[-13.8187, -4.6901, 3.4947]])
tensor([[inf, inf, inf],
[inf, inf, inf]])
tensor([[1., 1., 1.],
[1., 1., 1.]])
tensor([[1., 1., 1.],
[1., 1., 1.]])
torch.mul 是乘法 torch.div 是除法 torch.pow 是幂运算(特别的:零的零次方也是1)
import torch
a = torch.FloatTensor([[1, 2, 3], [3, 2, 1]])
b = torch.FloatTensor([[4, 5], [2, 7], [3, 1]])
print(torch.mm(a, b))
print(torch.mm(b, a))
c = torch.randn(3)
print(torch.mv(a, c))
tensor([[17., 22.],
[19., 30.]])
tensor([[19., 18., 17.],
[23., 18., 13.],
[ 6., 8., 10.]])
tensor([0.6090, 1.7420])
torch.mm 是矩阵乘法 torch.mv 是矩阵和向量的乘法(注意:数据类型要相同才能运算)
一个简单的神经网络
torch中 .t()是输出转置矩阵
format 函数可以接受不限个参数,位置可以不按顺序
如:"{1} {0} {1}".format("hello", "world") 输出结果为“'world hello world”
import torch
import matplotlib.pyplot as plt
%matplotlib inline
batch_n = 100 # 输入数据量
hidden_layer = 100 # 经隐藏层后的数据量
input_data = 1000 # 每个数据中有1000个数据特征
output_data = 10 # 输出10个分类结果
x = torch.randn(batch_n, input_data) # 100*1000
y = torch.randn(batch_n, output_data) # 100*10
w1 = torch.randn(input_data, hidden_layer) # 1000*100
w2 = torch.randn(hidden_layer, output_data) # 100*10
# 输入层到输出层的权重初始化定义
epoch_n = 20 # 学习次数
learning_rate = 1e-7 # 学习速率
for epoch in range(epoch_n):
h1 = x.mm(w1) # 100*100
h1 = h1.clamp(min=0) # 过滤
y_pred = h1.mm(w2) # 100*10 # 前向传播预测值
loss = (y_pred - y).pow(2).sum() # 误差值 均方误差函数
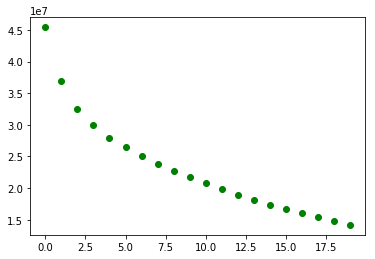
print("Epoch:{}, Loss:{:.4f}".format(epoch, loss))
plt.plot(epoch, loss/1000000, "g-.o")
grad_y_pred = 2*(y_pred - y)
grad_w2 = h1.t().mm(grad_y_pred) # 链式求导梯度
grad_h = grad_y_pred.clone()
grad_h = grad_h.mm(w2.t())
grad_h.clamp_(min=0)
grad_w1 = x.t().mm(grad_h) # 链式求导梯度
w1 -= learning_rate*grad_w1 # 新权重
w2 -= learning_rate*grad_w2 # 新权重
Epoch:0, Loss:46159204.0000
Epoch:1, Loss:35363124.0000
Epoch:2, Loss:30140088.0000
Epoch:3, Loss:27308764.0000
Epoch:4, Loss:25534646.0000
Epoch:5, Loss:24247540.0000
Epoch:6, Loss:23200030.0000
Epoch:7, Loss:22282628.0000
Epoch:8, Loss:21446886.0000
Epoch:9, Loss:20668928.0000
Epoch:10, Loss:19937316.0000
Epoch:11, Loss:19245446.0000
Epoch:12, Loss:18589512.0000
Epoch:13, Loss:17966258.0000
Epoch:14, Loss:17373192.0000
Epoch:15, Loss:16808334.0000
Epoch:16, Loss:16270253.0000
Epoch:17, Loss:15757100.0000
Epoch:18, Loss:15267285.0000
Epoch:19, Loss:14799396.0000
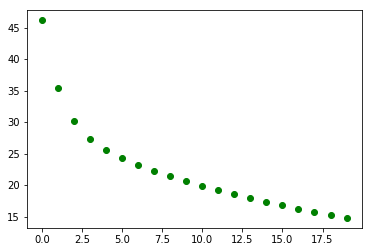
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
%matplotlib inline
batch_n = 100 # 输入数据量
hidden_layer = 100 # 经隐藏层后的数据量
input_data = 1000 # 每个数据中有1000个数据特征
output_data = 10 # 输出10个分类结果
x = Variable(torch.randn(batch_n, input_data),requires_grad=False) # 100*1000
y = Variable(torch.randn(batch_n, output_data),requires_grad=False) # 100*10
w1 = Variable(torch.randn(input_data, hidden_layer),requires_grad=True) # 1000*100
w2 = Variable(torch.randn(hidden_layer, output_data),requires_grad=True) # 100*10
# 输入层到输出层的权重初始化定义
# Variable封装 且w1 w2保留梯度值
epoch_n = 20 # 学习次数
learning_rate = 1e-7 # 学习速率
for epoch in range(epoch_n):
y_pred = x.mm(w1).clamp(min=0).mm(w2)
loss = (y_pred - y).pow(2).sum() # 误差值 均方误差函数
print("Epoch:{}, Loss:{:.4f}".format(epoch, loss.item()))
plt.plot(epoch, loss.item(), "g-.o")
loss.backward()
w1.data -= learning_rate*w1.grad.data # 新权重
w2.data -= learning_rate*w2.grad.data # 新权重
w1.grad.data.zero_()
w2.grad.data.zero_()
Epoch:0, Loss:45419716.0000
Epoch:1, Loss:36970548.0000
Epoch:2, Loss:32581012.0000
Epoch:3, Loss:29904798.0000
Epoch:4, Loss:27988124.0000
Epoch:5, Loss:26438394.0000
Epoch:6, Loss:25090844.0000
Epoch:7, Loss:23873752.0000
Epoch:8, Loss:22752522.0000
Epoch:9, Loss:21709780.0000
Epoch:10, Loss:20735070.0000
Epoch:11, Loss:19820292.0000
Epoch:12, Loss:18961622.0000
Epoch:13, Loss:18154286.0000
Epoch:14, Loss:17393844.0000
Epoch:15, Loss:16677597.0000
Epoch:16, Loss:16001947.0000
Epoch:17, Loss:15363768.0000
Epoch:18, Loss:14760480.0000
Epoch:19, Loss:14189733.0000