神经网络优化篇:详解梯度检验(Gradient checking)
梯度检验
梯度检验帮节省了很多时间,也多次帮发现backprop实施过程中的bug,接下来,看看如何利用它来调试或检验backprop的实施是否正确。
假设的网络中含有下列参数,\(W^{[1]}\)和\(b^{[1]}\)……\(W^{[l]}\)和\(b^{[l]}\),为了执行梯度检验,首先要做的就是,把所有参数转换成一个巨大的向量数据,要做的就是把矩阵\(W\)转换成一个向量,把所有\(W\)矩阵转换成向量之后,做连接运算,得到一个巨型向量\(\theta\),该向量表示为参数\(\theta\),代价函数\(J\)是所有\(W\)和\(b\)的函数,现在得到了一个\(\theta\)的代价函数\(J\)(即\(J(\theta)\))。接着,得到与\(W\)和\(b\)顺序相同的数据,同样可以把\(dW^{[1]}\)和\({db}^{[1]}\)……\({dW}^{[l]}\)和\({db}^{[l]}\)转换成一个新的向量,用它们来初始化大向量\(d\theta\),它与\(\theta\)具有相同维度。
同样的,把\(dW^{[1]}\)转换成矩阵,\(db^{[1]}\)已经是一个向量了,直到把\({dW}^{[l]}\)转换成矩阵,这样所有的\(dW\)都已经是矩阵,注意\(dW^{[1]}\)与\(W^{[1]}\)具有相同维度,\(db^{[1]}\)与\(b^{[1]}\)具有相同维度。经过相同的转换和连接运算操作之后,可以把所有导数转换成一个大向量\(d\theta\),它与\(\theta\)具有相同维度,现在的问题是\(d\theta\)和代价函数\(J\)的梯度或坡度有什么关系?

这就是实施梯度检验的过程,英语里通常简称为“grad check”,首先,要清楚\(J\)是超参数\(\theta\)的一个函数,也可以将J函数展开为\(J(\theta_{1},\theta_{2},\theta_{3},\ldots\ldots)\),不论超级参数向量\(\theta\)的维度是多少,为了实施梯度检验,要做的就是循环执行,从而对每个\(i\)也就是对每个\(\theta\)组成元素计算\(d\theta_{\text{approx}}[i]\)的值,使用双边误差,也就是
\(d\theta_{\text{approx}}\left[i \right] = \frac{J\left( \theta_{1},\theta_{2},\ldots\theta_{i} + \varepsilon,\ldots \right) - J\left( \theta_{1},\theta_{2},\ldots\theta_{i} - \varepsilon,\ldots \right)}{2\varepsilon}\)
只对\(\theta_{i}\)增加\(\varepsilon\),其它项保持不变,因为使用的是双边误差,对另一边做同样的操作,只不过是减去\(\varepsilon\),\(\theta\)其它项全都保持不变。

之前了解到这个值(\(d\theta_{\text{approx}}\left[i \right]\))应该逼近\(d\theta\left[i \right]\)=\(\frac{\partial J}{\partial\theta_{i}}\),\(d\theta\left[i \right]\)是代价函数的偏导数,然后需要对i的每个值都执行这个运算,最后得到两个向量,得到\(d\theta\)的逼近值\(d\theta_{\text{approx}}\),它与\(d\theta\)具有相同维度,它们两个与\(\theta\)具有相同维度,要做的就是验证这些向量是否彼此接近。

具体来说,如何定义两个向量是否真的接近彼此?一般做下列运算,计算这两个向量的距离,\(d\theta_{\text{approx}}\left[i \right] - d\theta[i]\)的欧几里得范数,注意这里(\({||d\theta_{\text{approx}} -d\theta||}_{2}\))没有平方,它是误差平方之和,然后求平方根,得到欧式距离,然后用向量长度归一化,使用向量长度的欧几里得范数。分母只是用于预防这些向量太小或太大,分母使得这个方程式变成比率,实际执行这个方程式,\(\varepsilon\)可能为\(10^{-7}\),使用这个取值范围内的\(\varepsilon\),如果发现计算方程式得到的值为\(10^{-7}\)或更小,这就很好,这就意味着导数逼近很有可能是正确的,它的值非常小。
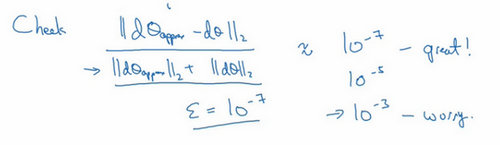
如果它的值在\(10^{-5}\)范围内,就要小心了,也许这个值没问题,但会再次检查这个向量的所有项,确保没有一项误差过大,可能这里有bug。
如果左边这个方程式结果是\(10^{-3}\),就会担心是否存在bug,计算结果应该比\(10^{- 3}\)小很多,如果比\(10^{-3}\)大很多,就会很担心,担心是否存在bug。这时应该仔细检查所有\(\theta\)项,看是否有一个具体的\(i\)值,使得\(d\theta_{\text{approx}}\left[i \right]\)与$ d\theta[i]$大不相同,并用它来追踪一些求导计算是否正确,经过一些调试,最终结果会是这种非常小的值(\(10^{-7}\)),那么,的实施可能是正确的。

在实施神经网络时,经常需要执行foreprop和backprop,然后可能发现这个梯度检验有一个相对较大的值,会怀疑存在bug,然后开始调试,调试,调试,调试一段时间后,得到一个很小的梯度检验值,现在可以很自信的说,神经网络实施是正确的。





