神经网络入门篇:详解搭建神经网络块(Building blocks of deep neural networks)
搭建神经网络块
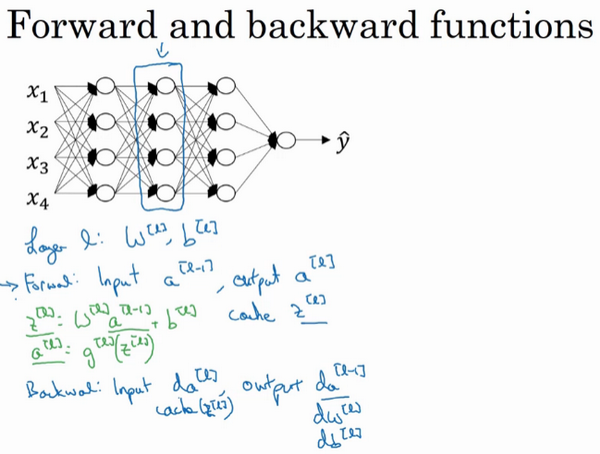
这是一个层数较少的神经网络,选择其中一层(方框部分),从这一层的计算着手。在第\(l\)层有参数\(W^{[l]}\)和\(b^{[l]}\),正向传播里有输入的激活函数,输入是前一层\(a^{[l-1]}\),输出是\(a^{[l]}\),之前讲过\(z^{[l]} =W^{[l]}a^{[l-1]} +b^{[l]}\),\(a^{[l]} =g^{[l]}(z^{[l]})\),那么这就是如何从输入\(a^{[l-1]}\)走到输出的\(a^{[l]}\)。之后就可以把\(z^{[l]}\)的值缓存起来,在这里也会把这包括在缓存中,因为缓存的\(z^{[i]}\)对以后的正向反向传播的步骤非常有用。
然后是反向步骤或者说反向传播步骤,同样也是第\(l\)层的计算,会需要实现一个函数输入为\(da^{[l]}\),输出\(da^{[l-1]}\)的函数。一个小细节需要注意,输入在这里其实是\(da^{[l]}\)以及所缓存的\(z^{[l]}\)值,之前计算好的\(z^{[l]}\)值,除了输出\(da^{[l-1]}\)的值以外,也需要输出需要的梯度\(dW^{[l]}\)和\(db^{[l]}\),这是为了实现梯度下降学习。
这就是基本的正向步骤的结构,把它成为称为正向函数,类似的在反向步骤中会称为反向函数。总结起来就是,在l层,会有正向函数,输入\(a^{[l-1]}\)并且输出\(a^{[l]}\),为了计算结果需要用\(W^{[l]}\)和\(b^{[l]}\),以及输出到缓存的\(z^{[l]}\)。然后用作反向传播的反向函数,是另一个函数,输入\(da^{[l]}\),输出\(da^{[l-1]}\),就会得到对激活函数的导数,也就是希望的导数值\(da^{[l]}\)。\(a^{[l-1]}\)是会变的,前一层算出的激活函数导数。在这个方块(第二个)里需要\(W^{[l]}\)和\(b^{[l]}\),最后要算的是\(dz^{[l]}\)。然后这个方块(第三个)中,这个反向函数可以计算输出\(dW^{[l]}\)和\(db^{[l]}\)。
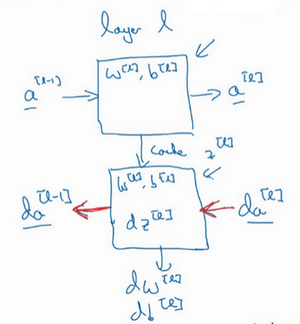
然后如果实现了这两个函数(正向和反向),然后神经网络的计算过程会是这样的:
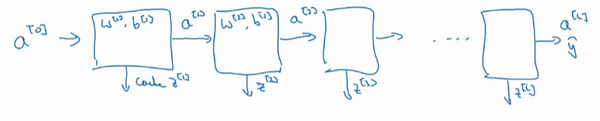
把输入特征\(a^{[0]}\),放入第一层并计算第一层的激活函数,用\(a^{[1]}\)表示,需要\(W^{[1]}\)和\(b^{[1]}\)来计算,之后也缓存\(z^{[l]}\)值。之后喂到第二层,第二层里,需要用到\(W^{[2]}\)和\(b^{[2]}\),会需要计算第二层的激活函数\(a^{[2]}\)。后面几层以此类推,直到最后算出了\(a^{[L]}\),第\(L\)层的最终输出值\(\hat y\)。在这些过程里缓存了所有的\(z\)值,这就是正向传播的步骤。
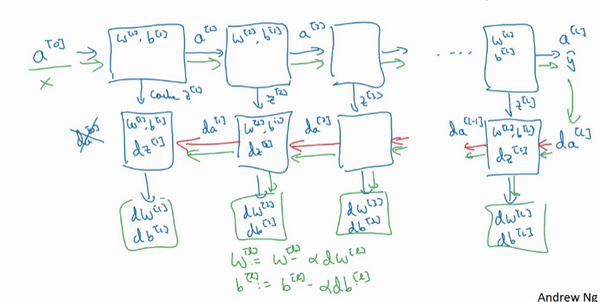
对反向传播的步骤而言,需要算一系列的反向迭代,就是这样反向计算梯度,需要把\(da^{[L]}\)的值放在这里,然后这个方块会给\({da}^{[L-1]}\)的值,以此类推,直到得到\({da}^{[2]}\)和\({da}^{[1]}\),还可以计算多一个输出值,就是\({da}^{[0]}\),但这其实是的输入特征的导数,并不重要,起码对于训练监督学习的权重不算重要,可以止步于此。反向传播步骤中也会输出\(dW^{[l]}\)和\(db^{[l]}\),这会输出\(dW^{[3]}\)和\(db^{[3]}\)等等。
神经网络的一步训练包含了,从\(a^{[0]}\)开始,也就是 \(x\) 然后经过一系列正向传播计算得到\(\hat y\),之后再用输出值计算这个(第二行最后方块),再实现反向传播。现在就有所有的导数项了,\(W\)也会在每一层被更新为\(W=W-αdW\),\(b\)也一样,\(b=b-αdb\),反向传播就都计算完毕,有所有的导数值,那么这是神经网络一个梯度下降循环。
继续下去之前再补充一个细节,概念上会非常有帮助,那就是把反向函数计算出来的\(z\)值缓存下来。当做编程练习的时候去实现它时,会发现缓存可能很方便,可以迅速得到\(W^{[l]}\)和\(b^{[l]}\)的值,非常方便的一个方法,在编程练习中缓存了\(z\),还有\(W\)和\(b\)对吧?从实现角度上看,认为是一个很方便的方法,可以将参数复制到在计算反向传播时所需要的地方。
现在们见过实现深度神经网络的基本元件,在每一层中有一个正向传播步骤,以及对应的反向传播步骤,以及把信息从一步传递到另一步的缓存。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号