神经网络入门篇：详解多样本向量化（Vectorizing across multiple examples）

多样本向量化

• 与上篇博客相联系的来理解

逻辑回归是将各个训练样本组合成矩阵，对矩阵的各列进行计算。神经网络是通过对逻辑回归中的等式简单的变形，让神经网络计算出输出值。这种计算是所有的训练样本同时进行的，以下是实现它具体的步骤：

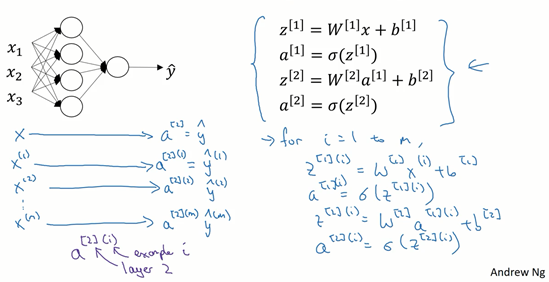
图1.4.1

上篇博客中得到的四个等式。它们给出如何计算出\(z^{[1]}\)，\(a^{[1]}\)，\(z^{[2]}\)，\(a^{[2]}\)。

对于一个给定的输入特征向量\(X\)，这四个等式可以计算出\(\alpha^{[2]}\)等于\(\hat{y}\)。这是针对于单一的训练样本。如果有\(m\)个训练样本,那么就需要重复这个过程。

用第一个训练样本\(x^{[1]}\)来计算出预测值\(\hat{y}^{[1]}\)，就是第一个训练样本上得出的结果。

然后，用\(x^{[2]}\)来计算出预测值\(\hat{y}^{[2]}\)，循环往复，直至用\(x^{[m]}\)计算出\(\hat{y}^{[m]}\)。

用激活函数表示法，如上图左下所示，它写成\(a^{[2](1)}\)、\(a^{[2](2)}\)和\(a^{[2](m)}\)。

【注】：\(a^{[2](i)}\)，\((i)\)是指第\(i\)个训练样本而\([2]\)是指第二层。

如果有一个非向量化形式的实现，而且要计算出它的预测值，对于所有训练样本，需要让\(i\)从1到\(m\)实现这四个等式：

\(z^{[1](i)}=W^{[1](i)}x^{(i)}+b^{[1](i)}\)

\(a^{[1](i)}=\sigma(z^{[1](i)})\)

\(z^{[2](i)}=W^{[2](i)}a^{[1](i)}+b^{[2](i)}\)

\(a^{[2](i)}=\sigma(z^{[2](i)})\)

对于上面的这个方程中的\(^{(i)}\)，是所有依赖于训练样本的变量，即将\((i)\)添加到\(x\)，\(z\)和\(a\)。如果想计算\(m\)个训练样本上的所有输出，就应该向量化整个计算，以简化这列。

这里需要使用很多线性代数的内容，重要的是能够正确地实现这一点，尤其是在深度学习的错误中。实际上我认真地选择了运算符号，这些符号只是针对于我所写神经网络系列的博客的，并且能使这些向量化容易一些。

所以，希望通过这个细节可以更快地正确实现这些算法。接下来讲讲如何向量化这些：
公式1.12：

\[x = \left[ \begin{array}{c} \vdots & \vdots & \vdots & \vdots\\ x^{(1)} & x^{(2)} & \cdots & x^{(m)}\\ \vdots & \vdots & \vdots & \vdots\\ \end{array} \right] \]

公式1.13：

\[Z^{[1]} = \left[ \begin{array}{c} \vdots & \vdots & \vdots & \vdots\\ z^{[1](1)} & z^{[1](2)} & \cdots & z^{[1](m)}\\ \vdots & \vdots & \vdots & \vdots\\ \end{array} \right] \]

公式1.14：

\[A^{[1]} = \left[ \begin{array}{c} \vdots & \vdots & \vdots & \vdots\\ \alpha^{[1](1)} & \alpha^{[1](2)} & \cdots & \alpha^{[1](m)}\\ \vdots & \vdots & \vdots & \vdots\\ \end{array} \right] \]

公式1.15：

\[\left. \begin{array}{r} \text{$z^{[1](i)} = W^{[1](i)}x^{(i)} + b^{[1]}$}\\ \text{$\alpha^{[1](i)} = \sigma(z^{[1](i)})$}\\ \text{$z^{[2](i)} = W^{[2](i)}\alpha^{[1](i)} + b^{[2]}$}\\ \text{$\alpha^{[2](i)} = \sigma(z^{[2](i)})$}\\ \end{array} \right\} \implies \begin{cases} \text{$A^{[1]} = \sigma(z^{[1]})$}\\ \text{$z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$}\\ \text{$A^{[2]} = \sigma(z^{[2]})$}\\ \end{cases} \]

定义矩阵\(X\)等于训练样本，将它们组合成矩阵的各列，形成一个\(n\)维或\(n\)乘以\(m\)维矩阵。接下来计算见公式1.15：

以此类推，从小写的向量\(x\)到这个大写的矩阵\(X\)，只是通过组合\(x\)向量在矩阵的各列中。

同理，\(z^{[1](1)}\)，\(z^{[1](2)}\)等等都是\(z^{[1](m)}\)的列向量，将所有\(m\)都组合在各列中，就的到矩阵\(Z^{[1]}\)。

同理，\(a^{[1](1)}\)，\(a^{[1](2)}\)，……，\(a^{[1](m)}\)将其组合在矩阵各列中，如同从向量\(x\)到矩阵\(X\)，以及从向量\(z\)到矩阵\(Z\)一样，就能得到矩阵\(A^{[1]}\)。

同样的，对于\(Z^{[2]}\)和\(A^{[2]}\)，也是这样得到。

这种符号其中一个作用就是，可以通过训练样本来进行索引。这就是水平索引对应于不同的训练样本的原因，这些训练样本是从左到右扫描训练集而得到的。

在垂直方向，这个垂直索引对应于神经网络中的不同节点。例如，这个节点，该值位于矩阵的最左上角对应于激活单元，它是位于第一个训练样本上的第一个隐藏单元。它的下一个值对应于第二个隐藏单元的激活值。它是位于第一个训练样本上的，以及第一个训练示例中第三个隐藏单元，等等。

当垂直扫描，是索引到隐藏单位的数字。当水平扫描，将从第一个训练示例中从第一个隐藏的单元到第二个训练样本，第三个训练样本……直到节点对应于第一个隐藏单元的激活值，且这个隐藏单元是位于这\(m\)个训练样本中的最终训练样本。

从水平上看，矩阵\(A\)代表了各个训练样本。从竖直上看，矩阵\(A\)的不同的索引对应于不同的隐藏单元。

对于矩阵\(Z，X\)情况也类似，水平方向上，对应于不同的训练样本；竖直方向上，对应不同的输入特征，而这就是神经网络输入层中各个节点。

神经网络上通过在多样本情况下的向量化来使用这些等式。