神经网络基础篇:关于 python_numpy 向量的说明(A note on python or numpy vectors)
关于 python_numpy 向量的说明
- 主要讲Python中的numpy一维数组的特性,以及与行向量或列向量的区别。并说一下在实际应用中的一些小技巧,去避免在coding中由于这些特性而导致的bug
Python的特性允许使用广播(broadcasting)功能,这是Python的numpy程序语言库中最灵活的地方。而本人认为这是程序语言的优点,也是缺点。优点的原因在于它们创造出语言的表达性,Python语言巨大的灵活性使得仅仅通过一行代码就能做很多事情。但是这也是缺点,由于广播巨大的灵活性,有时候对于广播的特点以及广播的工作原理这些细节不熟悉的话,可能会产生很细微或者看起来很奇怪的bug。例如,如果将一个列向量添加到一个行向量中,会以为它报出维度不匹配或类型错误之类的错误,但是实际上会得到一个行向量和列向量的求和。
在Python的这些奇怪的影响之中,其实是有一个内在的逻辑关系的。但是如果对Python不熟悉的话,本人就曾经见过的一些一些人非常生硬、非常艰难地去寻找bug。所以本人在这里想做的就是分享给们一些技巧,这些技巧非常有用,它们能消除或者简化代码中所有看起来很奇怪的bug。同时也希望通过这些技巧,也能更容易地写没有bug的Python和numpy代码。
为了演示Python-numpy的一个容易被忽略的效果,特别是怎样在Python-numpy中构造向量,来做一个快速示范。首先设置\(a=np.random.randn(5)\),这样会生成存储在数组 \(a\) 中的5个高斯随机数变量。之后输出 \(a\),可以得知,此时 \(a\) 的shape(形状)是一个\((5,)\)的结构。这在Python中被称作一个一维数组。它既不是一个行向量也不是一个列向量,这也导致它有一些不是很直观的效果。举个例子,如果输出一个转置阵,最终结果它会和\(a\)看起来一样,所以\(a\)和\(a\)的转置阵最终结果看起来一样。而如果输出\(a\)和\(a\)的转置阵的内积,可能会想:\(a\)乘以\(a\)的转置返回给的可能会是一个矩阵。但是如果这样做,只会得到一个数。
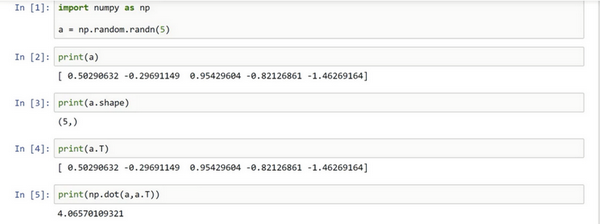
所以建议编写神经网络时,不要使用shape为 (5,)、(n,) 或者其他一维数组的数据结构。相反,如果设置 \(a\) 为\((5,1)\),那么这就将置于5行1列向量中。在先前的操作里 \(a\) 和 \(a\) 的转置看起来一样,而现在这样的 \(a\) 变成一个新的 \(a\) 的转置,并且它是一个行向量。请注意一个细微的差别,在这种数据结构中,当输出 \(a\) 的转置时有两对方括号,而之前只有一对方括号,所以这就是1行5列的矩阵和一维数组的差别。
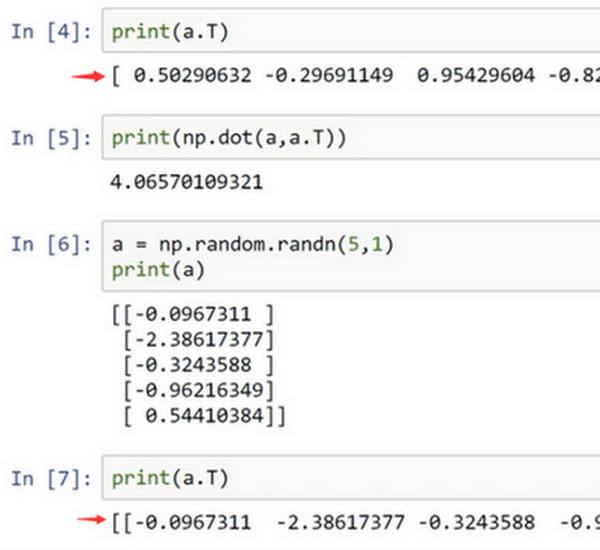
如果输出 \(a\) 和 \(a\) 的转置的乘积,然后会返回给一个向量的外积,是吧?所以这两个向量的外积返回给的是一个矩阵。
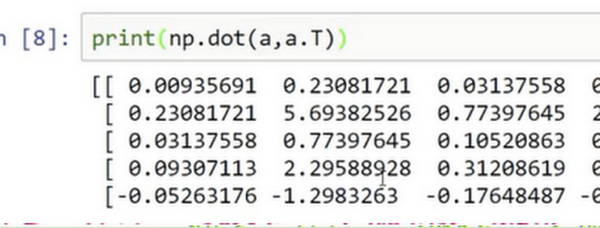
就刚才看到的,再进一步说明。首先刚刚运行的命令是这个 \((a=np.random.randn(5))\),它生成了一个数据结构\(a\),其中\(a.shape\)是\((5,)\)。这被称作 \(a\) 的一维数组,同时这也是一个非常有趣的数据结构。它不像行向量和列向量那样表现的很一致,这使得它带来一些不直观的影响。所以本人建议,当在编程练习或者在执行逻辑回归和神经网络时,不需要使用这些一维数组。

相反,如果每次创建一个数组,都得让它成为一个列向量,产生一个\((5,1)\)向量或者让它成为一个行向量,那么的向量的行为可能会更容易被理解。所以在这种情况下,\(a.shape\)等同于\((5,1)\)。这种表现很像 \(a\),但是实际上却是一个列向量。同时这也是为什么当它是一个列向量的时候,能认为这是矩阵\((5,1)\);同时这里 \(a.shape\) 将要变成\((1,5)\),这就像行向量一样。所以当需要一个向量时,本人会说用这个或那个(column vector or row vector),但绝不会是一维数组。

本人写代码时还有一件经常做的事,那就是如果不完全确定一个向量的维度(dimension),经常会扔进一个断言语句(assertion statement)。像这样,去确保在这种情况下是一个\((5,1)\)向量,或者说是一个列向量。这些断言语句实际上是要去执行的,并且它们也会有助于为的代码提供信息。所以不论要做什么,不要犹豫直接插入断言语句。如果不小心以一维数组来执行,也能够重新改变数组维数 \(a=reshape\),表明一个\((5,1)\)数组或者一个\((1,5)\)数组,以致于它表现更像列向量或行向量。

有时候看见一些人因为一维数组不直观的影响,难以定位bug而告终。通过在原先的代码里清除一维数组,代码变得更加简洁。而且实际上就在代码中表现的事情而言,本人从来不使用一维数组。因此,要去简化的代码,而且不要使用一维数组。总是使用 \(n \times 1\) 维矩阵(基本上是列向量),或者 \(1 \times n\) 维矩阵(基本上是行向量),这样可以减少很多assert语句来节省核矩阵和数组的维数的时间。另外,为了确保的矩阵或向量所需要的维数时,不要羞于 reshape 操作。
总之,本人希望这些建议能帮助解决一个Python中的bug。



